
In mathematics, the Fibonacci numbers, commonly denoted Fn , form a sequence, the Fibonacci sequence, in which each number is the sum of the two preceding ones. The sequence commonly starts from 0 and 1, although some authors start the sequence from 1 and 1 or sometimes from 1 and 2. Starting from 0 and 1, the first few values in the sequence are:
In number theory, the Fermat pseudoprimes make up the most important class of pseudoprimes that come from Fermat's little theorem.
2 (two) is a number, numeral and digit. It is the natural number following 1 and preceding 3. It is the smallest and only even prime number. Because it forms the basis of a duality, it has religious and spiritual significance in many cultures.
A highly composite number is a positive integer with more divisors than any smaller positive integer has. A related concept is that of a largely composite number, a positive integer which has at least as many divisors as any smaller positive integer. The name can be somewhat misleading, as the first two highly composite numbers are not actually composite numbers; however, all further terms are.
21 (twenty-one) is the natural number following 20 and preceding 22.
In recreational mathematics, a repdigit or sometimes monodigit is a natural number composed of repeated instances of the same digit in a positional number system. The word is a portmanteau of repeated and digit. Examples are 11, 666, 4444, and 999999. All repdigits are palindromic numbers and are multiples of repunits. Other well-known repdigits include the repunit primes and in particular the Mersenne primes.
In mathematics, and more particularly in number theory, primorial, denoted by "#", is a function from natural numbers to natural numbers similar to the factorial function, but rather than successively multiplying positive integers, the function only multiplies prime numbers.
4000 is the natural number following 3999 and preceding 4001. It is a decagonal number.

One million (1,000,000), or one thousand thousand, is the natural number following 999,999 and preceding 1,000,001. The word is derived from the early Italian millione, from mille, "thousand", plus the augmentative suffix -one.
Lucas pseudoprimes and Fibonacci pseudoprimes are composite integers that pass certain tests which all primes and very few composite numbers pass: in this case, criteria relative to some Lucas sequence.

In number theory, a practical number or panarithmic number is a positive integer such that all smaller positive integers can be represented as sums of distinct divisors of . For example, 12 is a practical number because all the numbers from 1 to 11 can be expressed as sums of its divisors 1, 2, 3, 4, and 6: as well as these divisors themselves, we have 5 = 3 + 2, 7 = 6 + 1, 8 = 6 + 2, 9 = 6 + 3, 10 = 6 + 3 + 1, and 11 = 6 + 3 + 2.

In mathematics, the Pell numbers are an infinite sequence of integers, known since ancient times, that comprise the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins 1/1, 3/2, 7/5, 17/12, and 41/29, so the sequence of Pell numbers begins with 1, 2, 5, 12, and 29. The numerators of the same sequence of approximations are half the companion Pell numbers or Pell–Lucas numbers; these numbers form a second infinite sequence that begins with 2, 6, 14, 34, and 82.

In number theory, Znám's problem asks which sets of integers have the property that each integer in the set is a proper divisor of the product of the other integers in the set, plus 1. Znám's problem is named after the Slovak mathematician Štefan Znám, who suggested it in 1972, although other mathematicians had considered similar problems around the same time.
100,000 (one hundred thousand) is the natural number following 99,999 and preceding 100,001. In scientific notation, it is written as 105.
In mathematics, a superabundant number is a certain kind of natural number. A natural number n is called superabundant precisely when, for all m < n

In number theory, a polite number is a positive integer that can be written as the sum of two or more consecutive positive integers. A positive integer which is not polite is called impolite. The impolite numbers are exactly the powers of two, and the polite numbers are the natural numbers that are not powers of two.

In number theory, Sylvester's sequence is an integer sequence in which each term is the product of the previous terms, plus one. The first few terms of the sequence are
In mathematics, the greedy algorithm for Egyptian fractions is a greedy algorithm, first described by Fibonacci, for transforming rational numbers into Egyptian fractions. An Egyptian fraction is a representation of an irreducible fraction as a sum of distinct unit fractions, such as 5/6 = 1/2 + 1/3. As the name indicates, these representations have been used as long ago as ancient Egypt, but the first published systematic method for constructing such expansions was described in 1202 in the Liber Abaci of Leonardo of Pisa (Fibonacci). It is called a greedy algorithm because at each step the algorithm chooses greedily the largest possible unit fraction that can be used in any representation of the remaining fraction.
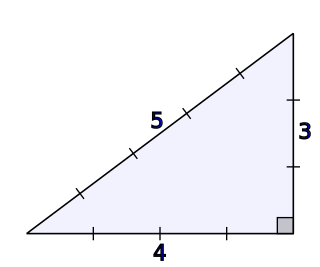
In mathematics, a nonhypotenuse number is a natural number whose square cannot be written as the sum of two nonzero squares. The name stems from the fact that an edge of length equal to a nonhypotenuse number cannot form the hypotenuse of a right angle triangle with integer sides.
In number theory, reversing the digits of a number n sometimes produces another number m that is divisible by n. This happens trivially when n is a palindromic number; the nontrivial reverse divisors are






















