Related Research Articles
Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics to astronomical objects, such as stars and planets, to produce ephemeris data.
The year 1991 in science and technology involved many significant events, some listed below.

In physics and classical mechanics, the three-body problem is the problem of taking the initial positions and velocities of three point masses and solving for their subsequent motion according to Newton's laws of motion and Newton's law of universal gravitation. The three-body problem is a special case of the n-body problem. Unlike two-body problems, no general closed-form solution exists, as the resulting dynamical system is chaotic for most initial conditions, and numerical methods are generally required.
Georgij Albertovich Krasinsky was a Russian astronomer active at the Institute of Applied Astronomy, Russian Academy of Science, St Petersburg. He was notable for research on planetary motions and ephemerides.

Karl Frithiof Sundman was a Finnish mathematician who used analytic methods to prove the existence of a convergent infinite series solution to the three-body problem in two papers published in 1907 and 1909. His results gained fame when they were reproduced in Acta Mathematica in 1912. He also published a paper on regularization methods in mechanics in 1912.
Elena Vladimirovna Pitjeva is a Russian astronomer working at the Institute of Applied Astronomy, Russian Academy of Sciences, St. Petersburg. She has published over 100 articles, as listed in Google Scholar and the Astrophysics Data System in the field of solar system dynamics and celestial mechanics.
In physics, the n-body problem is the problem of predicting the individual motions of a group of celestial objects interacting with each other gravitationally. Solving this problem has been motivated by the desire to understand the motions of the Sun, Moon, planets, and visible stars. In the 20th century, understanding the dynamics of globular cluster star systems became an important n-body problem. The n-body problem in general relativity is considerably more difficult to solve due to additional factors like time and space distortions.
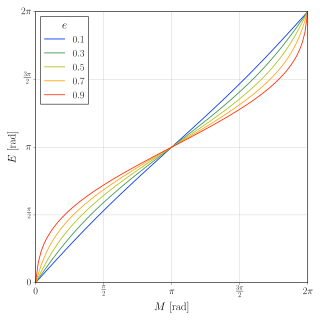
In orbital mechanics, Kepler's equation relates various geometric properties of the orbit of a body subject to a central force.
Michèle Moons (1951-1998) was a Belgian scientist, leading researches on Celestial Mechanics for the department of mathematics of Facultés Universitaires Notre Dame de la Paix in Namur (Belgium).

In physics, the Painlevé conjecture is a theorem about singularities among the solutions to the n-body problem: there are noncollision singularities for n ≥ 4.

Lai-Sang Lily Young is a Hong Kong-born American mathematician who holds the Henry & Lucy Moses Professorship of Science and is a professor of mathematics and neural science at the Courant Institute of Mathematical Sciences of New York University. Her research interests include dynamical systems, ergodic theory, chaos theory, probability theory, statistical mechanics, and neuroscience. She is particularly known for introducing the method of Markov returns in 1998, which she used to prove exponential correlation delay in Sinai billiards and other hyperbolic dynamical systems.
Richard Paul McGehee is an American mathematician, who works on dynamical systems with special emphasis on celestial mechanics.
Antti Kupiainen is a Finnish mathematical physicist.

Daniele Mortari is Professor of Aerospace Engineering at Texas A&M University and Chief Scientist for Space for Texas A&M ASTRO Center. Mortari is known for inventing the Flower Constellations and the k-vector range searching technique and the Theory of Functional Connections.
Zhihong "Jeff" Xia is a Chinese-American mathematician.
Antonio Giorgilli is an Italian mathematical physicist, known for his work on the perturbative theory of Hamiltonian systems with applications to studies of orbital stability for major and minor planets.
In celestial mechanics and the mathematics of the n-body problem, a central configuration is a system of point masses with the property that each mass is pulled by the combined gravitational force of the system directly towards the center of mass, with acceleration proportional to its distance from the center. Central configurations may be studied in Euclidean spaces of any dimension, although only dimensions one, two, and three are directly relevant for celestial mechanics.
Luigi Chierchia is an Italian mathematician, specializing in nonlinear differential equations, mathematical physics, and dynamical systems.

Valery Vasilevich Kozlov is a Russian mathematician and mathematical physicist.
Weak stability boundary (WSB), including low-energy transfer, is a concept introduced by Edward Belbruno in 1987. The concept explained how a spacecraft could change orbits using very little fuel.
References
- ↑ Home page of Qiudong Wang (University of Arizona, retrieved on 2007-05-05)
- ↑ Wang, Qiu Dong (1991), "The global solution of the n-body problem", Celestial Mechanics and Dynamical Astronomy, 50 (1): 73–88, Bibcode:1991CeMDA..50...73W, doi:10.1007/BF00048987, MR 1117788, S2CID 118132097 .
- ↑ Babadzanjanz, L. K. (1979), "Existence of the continuations in the N-body problem", Celestial Mechanics, 20 (1): 43–57, Bibcode:1979CeMec..20...43B, doi:10.1007/BF01236607, MR 0538663, S2CID 120358878 .
- ↑ Babadzanjanz, L. K. (1993), "On the global solution of the N-body problem", Celestial Mechanics and Dynamical Astronomy, 56 (3): 427–449, Bibcode:1993CeMDA..56..427B, doi:10.1007/BF00691812, MR 1225892, S2CID 120617936 .