In geometry, a secant of a curve is a line that intersects the curve in at least two (distinct) points. The word secant comes from the Latin word secare, meaning to cut. In the case of a circle, a secant will intersect the circle in exactly two points and a chord is the line segment determined by these two points, that is the interval on a secant whose endpoints are these points.
In mathematics, the canonical bundle of a non-singular algebraic variety of dimension over a field is the line bundle , which is the nth exterior power of the cotangent bundle Ω on V.
Gauss's lemma in number theory gives a condition for an integer to be a quadratic residue. Although it is not useful computationally, it has theoretical significance, being involved in some proofs of quadratic reciprocity.

In projective geometry an oval is a circle-like pointset (curve) in a plane that is defined by incidence properties. The standard examples are the nondegenerate conics. However, a conic is only defined in a pappian plane, whereas an oval may exist in any type of projective plane. In the literature, there are many criteria which imply that an oval is a conic, but there are many examples, both infinite and finite, of ovals in pappian planes which are not conics.

In projective geometry an ovoid is a sphere like pointset (surface) in a projective space of dimension d ≥ 3. Simple examples in a real projective space are hyperspheres (quadrics). The essential geometric properties of an ovoid are:
- Any line intersects in at most 2 points,
- The tangents at a point cover a hyperplane, and
- contains no lines.
In mathematics, a Minkowski plane is one of the Benz planes: Möbius plane, Laguerre plane and Minkowski plane.
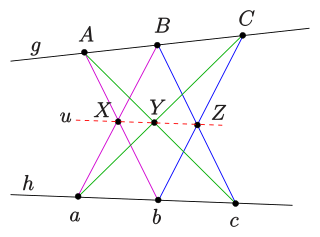
An (simple) arc in finite projective geometry is a set of points which satisfies, in an intuitive way, a feature of curved figures in continuous geometries. Loosely speaking, they are sets of points that are far from "line-like" in a plane or far from "plane-like" in a three-dimensional space. In this finite setting it is typical to include the number of points in the set in the name, so these simple arcs are called k-arcs. An important generalization of the k-arc concept, also referred to as arcs in the literature, are the -arcs.
In algebraic topology, a branch of mathematics, the Čech-to-derived functor spectral sequence is a spectral sequence that relates Čech cohomology of a sheaf and sheaf cohomology.

Galois geometry is the branch of finite geometry that is concerned with algebraic and analytic geometry over a finite field. More narrowly, a Galois geometry may be defined as a projective space over a finite field.
This is a glossary of algebraic geometry.

In mathematics, a Laguerre plane is one of the Benz planes: Möbius plane, Laguerre plane and Minkowski plane, named after the French mathematician Edmond Nicolas Laguerre.
In mathematics, a Möbius plane is one of the Benz planes: Möbius plane, Laguerre plane and Minkowski plane. The classical example is based on the geometry of lines and circles in the real affine plane.

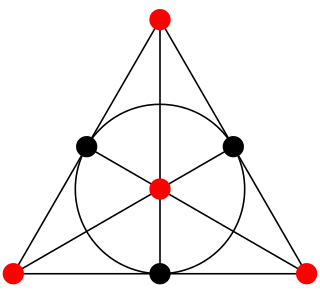
In geometry, the bundle theorem is in the simplest case a statement on six circles and eight points in the real Euclidean plane. In general it is a property of a Möbius plane that is fulfilled by ovoidal Möbius planes only.
In the mathematical field of algebraic number theory, the concept of principalization refers to a situation when, given an extension of algebraic number fields, some ideal of the ring of integers of the smaller field isn't principal but its extension to the ring of integers of the larger field is. Its study has origins in the work of Ernst Kummer on ideal numbers from the 1840s, who in particular proved that for every algebraic number field there exists an extension number field such that all ideals of the ring of integers of the base field become principal when extended to the larger field. In 1897 David Hilbert conjectured that the maximal abelian unramified extension of the base field, which was later called the Hilbert class field of the given base field, is such an extension. This conjecture, now known as principal ideal theorem, was proved by Philipp Furtwängler in 1930 after it had been translated from number theory to group theory by Emil Artin in 1929, who made use of his general reciprocity law to establish the reformulation. Since this long desired proof was achieved by means of Artin transfers of non-abelian groups with derived length two, several investigators tried to exploit the theory of such groups further to obtain additional information on the principalization in intermediate fields between the base field and its Hilbert class field. The first contributions in this direction are due to Arnold Scholz and Olga Taussky in 1934, who coined the synonym capitulation for principalization. Another independent access to the principalization problem via Galois cohomology of unit groups is also due to Hilbert and goes back to the chapter on cyclic extensions of number fields of prime degree in his number report, which culminates in the famous Theorem 94.

The Steiner conic or more precisely Steiner's generation of a conic, named after the Swiss mathematician Jakob Steiner, is an alternative method to define a non-degenerate projective conic section in a projective plane over a field.

In projective geometry Segre's theorem, named after the Italian mathematician Beniamino Segre, is the statement:
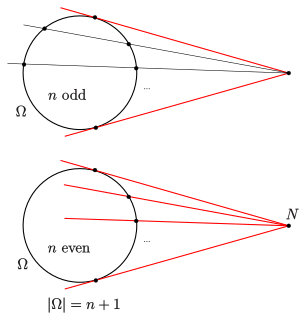
In projective geometry Qvist's theorem, named after the Finnish mathematician Bertil Qvist, is a statement on ovals in finite projective planes. Standard examples of ovals are non-degenerate (projective) conic sections. The theorem gives an answer to the question How many tangents to an oval can pass through a point in a finite projective plane? The answer depends essentially upon the order of the plane.
Topological geometry deals with incidence structures consisting of a point set and a family of subsets of called lines or circles etc. such that both and carry a topology and all geometric operations like joining points by a line or intersecting lines are continuous. As in the case of topological groups, many deeper results require the point space to be (locally) compact and connected. This generalizes the observation that the line joining two distinct points in the Euclidean plane depends continuously on the pair of points and the intersection point of two lines is a continuous function of these lines.