Quantum teleportation is a technique for transferring quantum information from a sender at one location to a receiver some distance away. While teleportation is commonly portrayed in science fiction as a means to transfer physical objects from one location to the next, quantum teleportation only transfers quantum information. The sender does not have to know the particular quantum state being transferred. Moreover, the location of the recipient can be unknown, but to complete the quantum teleportation, classical information needs to be sent from sender to receiver. Because classical information needs to be sent, quantum teleportation cannot occur faster than the speed of light.

Quantum entanglement is the phenomenon of a group of particles being generated, interacting, or sharing spatial proximity in such a way that the quantum state of each particle of the group cannot be described independently of the state of the others, including when the particles are separated by a large distance. The topic of quantum entanglement is at the heart of the disparity between classical and quantum physics: entanglement is a primary feature of quantum mechanics not present in classical mechanics.
Bell's theorem is a term encompassing a number of closely related results in physics, all of which determine that quantum mechanics is incompatible with local hidden-variable theories, given some basic assumptions about the nature of measurement. "Local" here refers to the principle of locality, the idea that a particle can only be influenced by its immediate surroundings, and that interactions mediated by physical fields cannot propagate faster than the speed of light. "Hidden variables" are supposed properties of quantum particles that are not included in quantum theory but nevertheless affect the outcome of experiments. In the words of physicist John Stewart Bell, for whom this family of results is named, "If [a hidden-variable theory] is local it will not agree with quantum mechanics, and if it agrees with quantum mechanics it will not be local."
In the interpretation of quantum mechanics, a local hidden-variable theory is a hidden-variable theory that satisfies the principle of locality. These models attempt to account for the probabilistic features of quantum mechanics via the mechanism of underlying, but inaccessible variables, with the additional requirement that distant events be statistically independent.

Anton Zeilinger is an Austrian quantum physicist and Nobel laureate in physics of 2022. Zeilinger is professor of physics emeritus at the University of Vienna and senior scientist at the Institute for Quantum Optics and Quantum Information of the Austrian Academy of Sciences. Most of his research concerns the fundamental aspects and applications of quantum entanglement.
The Peres–Horodecki criterion is a necessary condition, for the joint density matrix of two quantum mechanical systems and , to be separable. It is also called the PPT criterion, for positive partial transpose. In the 2×2 and 2×3 dimensional cases the condition is also sufficient. It is used to decide the separability of mixed states, where the Schmidt decomposition does not apply. The theorem was discovered in 1996 by Asher Peres and the Horodecki family
In quantum mechanics, separable states are multipartite quantum states that can be written as a convex combination of product states. Product states are multipartite quantum states that can be written as a tensor product of states in each space. The physical intuition behind these definitions is that product states have no correlation between the different degrees of freedom, while separable states might have correlations, but all such correlations can be explained as due to a classical random variable, as opposed as being due to entanglement.

LOCC, or local operations and classical communication, is a method in quantum information theory where a local (product) operation is performed on part of the system, and where the result of that operation is "communicated" classically to another part where usually another local operation is performed conditioned on the information received.

In physics, in the area of quantum information theory, a Greenberger–Horne–Zeilinger (GHZ) state is an entangled quantum state that involves at least three subsystems. Named for the three authors that first described this state, the GHZ state predicts outcomes from experiments that directly contradict predictions by every classical local Hidden-variable theory. The state has applications in quantum computing.
The W state is an entangled quantum state of three qubits which in the bra-ket notation has the following shape
Quantum cloning is a process that takes an arbitrary, unknown quantum state and makes an exact copy without altering the original state in any way. Quantum cloning is forbidden by the laws of quantum mechanics as shown by the no cloning theorem, which states that there is no operation for cloning any arbitrary state perfectly. In Dirac notation, the process of quantum cloning is described by:
In theoretical physics, quantum nonlocality refers to the phenomenon by which the measurement statistics of a multipartite quantum system do not allow an interpretation with local realism. Quantum nonlocality has been experimentally verified under a variety of physical assumptions.
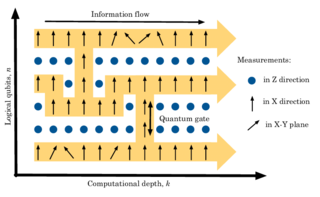
The one-way quantum computer, also known as measurement-based quantum computer (MBQC), is a method of quantum computing that first prepares an entangled resource state, usually a cluster state or graph state, then performs single qubit measurements on it. It is "one-way" because the resource state is destroyed by the measurements.
In quantum information and quantum computing, a cluster state is a type of highly entangled state of multiple qubits. Cluster states are generated in lattices of qubits with Ising type interactions. A cluster C is a connected subset of a d-dimensional lattice, and a cluster state is a pure state of the qubits located on C. They are different from other types of entangled states such as GHZ states or W states in that it is more difficult to eliminate quantum entanglement in the case of cluster states. Another way of thinking of cluster states is as a particular instance of graph states, where the underlying graph is a connected subset of a d-dimensional lattice. Cluster states are especially useful in the context of the one-way quantum computer. For a comprehensible introduction to the topic see.
In the case of systems composed of subsystems, the classification of quantum-entangledstates is richer than in the bipartite case. Indeed, in multipartite entanglement apart from fully separable states and fully entangled states, there also exists the notion of partially separable states.
Entanglement distillation is the transformation of N copies of an arbitrary entangled state into some number of approximately pure Bell pairs, using only local operations and classical communication.

Quantum complex networks are complex networks whose nodes are quantum computing devices. Quantum mechanics has been used to create secure quantum communications channels that are protected from hacking. Quantum communications offer the potential for secure enterprise-scale solutions.
Bound entanglement is a weak form of quantum entanglement, from which no singlets can be distilled with local operations and classical communication (LOCC).
In quantum physics, entanglement depth characterizes the strength of multiparticle entanglement. An entanglement depth means that the quantum state of a particle ensemble cannot be described under the assumption that particles interacted with each other only in groups having fewer than particles. It has been used to characterize the quantum states created in experiments with cold gases.
Bell diagonal states are a class of bipartite qubit states that are frequently used in quantum information and quantum computation theory.











