Related Research Articles
Quantum computing is the use of quantum phenomena such as superposition and entanglement to perform computation. Computers that perform quantum computations are known as quantum computers. Quantum computers are believed to be able to solve certain computational problems, such as integer factorization, substantially faster than classical computers. The study of quantum computing is a subfield of quantum information science.
This is a timeline of quantum computing.
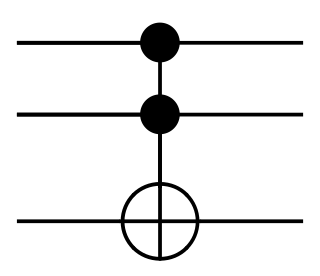
In logic circuits, the Toffoli gate, invented by Tommaso Toffoli, is a universal reversible logic gate, which means that any reversible circuit can be constructed from Toffoli gates. It is also known as the "controlled-controlled-not" gate, which describes its action. It has 3-bit inputs and outputs; if the first two bits are both set to 1, it inverts the third bit, otherwise all bits stay the same.
In quantum computing, a quantum algorithm is an algorithm which runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit model of computation. A classical algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a problem, where each step or instruction can be performed on a classical computer. Similarly, a quantum algorithm is a step-by-step procedure, where each of the steps can be performed on a quantum computer. Although all classical algorithms can also be performed on a quantum computer, the term quantum algorithm is usually used for those algorithms which seem inherently quantum, or use some essential feature of quantum computation such as quantum superposition or quantum entanglement.
A topological quantum computer is a theoretical quantum computer proposed by Russian-American physicist Alexei Kitaev in 1997. It employs two-dimensional quasiparticles called anyons, whose world lines pass around one another to form braids in a three-dimensional spacetime. These braids form the logic gates that make up the computer. The advantage of a quantum computer based on quantum braids over using trapped quantum particles is that the former is much more stable. Small, cumulative perturbations can cause quantum states to decohere and introduce errors in the computation, but such small perturbations do not change the braids' topological properties. This is like the effort required to cut a string and reattach the ends to form a different braid, as opposed to a ball bumping into a wall.
In quantum computing, the Gottesman–Knill theorem is a theoretical result by Daniel Gottesman and Emanuel Knill that states that stabilizer circuits, circuits that only consist of gates from the normalizer of the qubit Pauli group, also called Clifford group, can be perfectly simulated in polynomial time on a probabilistic classical computer. The Clifford group can be generated solely by using CNOT, Hadamard, and phase gates; and therefore stabilizer circuits can be constructed using only these gates.
Reservoir computing is a framework for computation derived from recurrent neural network theory that maps input signals into higher dimensional computational spaces through the dynamics of a fixed, non-linear system called a reservoir. After the input signal is fed into the reservoir, which is treated as a "black box," a simple readout mechanism is trained to read the state of the reservoir and map it to the desired output. The first key benefit of this framework is that training is performed only at the readout stage, as the reservoir dynamics are fixed. The second is that the computational power of naturally available systems, both classical and quantum mechanical, can be utilized to reduce the effective computational cost.
Daniel Amihud Lidar is the holder of the Viterbi Professorship of Engineering at the University of Southern California, where he is a Professor of Electrical Engineering, Chemistry, Physics & Astronomy. He is the Director and co-founder of the USC Center for Quantum Information Science & Technology (CQIST) as well as Scientific Director of the USC-Lockheed Martin Quantum Computing Center, notable for his research on control of quantum systems and quantum information processing.

David Matthew Ceperley is a theoretical physicist in the physics department at the University of Illinois Urbana-Champaign or UIUC. He is a world expert in the area of Quantum Monte Carlo computations, a method of calculation that is generally recognised to provide accurate quantitative results for many-body problems described by quantum mechanics.
Quantum cryptography is the science of exploiting quantum mechanical properties to perform cryptographic tasks. The best known example of quantum cryptography is quantum key distribution which offers an information-theoretically secure solution to the key exchange problem. The advantage of quantum cryptography lies in the fact that it allows the completion of various cryptographic tasks that are proven or conjectured to be impossible using only classical communication. For example, it is impossible to copy data encoded in a quantum state. If one attempts to read the encoded data, the quantum state will be changed due to wave function collapse. This could be used to detect eavesdropping in quantum key distribution.

Quantum machine learning is the integration of quantum algorithms within machine learning programs. The most common use of the term refers to machine learning algorithms for the analysis of classical data executed on a quantum computer, i.e. quantum-enhanced machine learning. While machine learning algorithms are used to compute immense quantities of data, quantum machine learning utilizes qubits and quantum operations or specialized quantum systems to improve computational speed and data storage done by algorithms in a program. This includes hybrid methods that involve both classical and quantum processing, where computationally difficult subroutines are outsourced to a quantum device. These routines can be more complex in nature and executed faster on a quantum computer. Furthermore, quantum algorithms can be used to analyze quantum states instead of classical data. Beyond quantum computing, the term "quantum machine learning" is also associated with classical machine learning methods applied to data generated from quantum experiments, such as learning the phase transitions of a quantum system or creating new quantum experiments. Quantum machine learning also extends to a branch of research that explores methodological and structural similarities between certain physical systems and learning systems, in particular neural networks. For example, some mathematical and numerical techniques from quantum physics are applicable to classical deep learning and vice versa. Furthermore, researchers investigate more abstract notions of learning theory with respect to quantum information, sometimes referred to as "quantum learning theory".
The USC-Lockheed Martin Quantum Computing Center (QCC) is a joint scientific research effort between Lockheed Martin Corporation and the University of Southern California (USC). The QCC is housed at the Information Sciences Institute (ISI), a computer science and engineering research unit of the USC Viterbi School of Engineering, and is jointly operated by ISI and Lockheed Martin.
Andrew MacGregor Childs is an American computer scientist and physicist known for his work on quantum computing. He is currently a Professor in the Department of Computer Science and Institute for Advanced Computer Studies at the University of Maryland. He also co-directs the Joint Center for Quantum Information and Computer Science, a partnership between the University of Maryland and the National Institute of Standards and Technology.
Quantum image processing (QIMP) is primarily devoted to using quantum computing and quantum information processing to create and work with quantum images. Due to some of the astounding properties inherent to quantum computation, notably entanglement and parallelism, it is anticipated that QIP technologies will offer capabilities and performances that are, as yet, unrivaled by their traditional equivalents. These improvements could be in terms of computing speed, guaranteed security, and minimal storage requirements, etc.
In quantum computing, quantum supremacy or quantum advantage is the goal of demonstrating that a programmable quantum device can solve a problem that no classical computer can solve in any feasible amount of time. Conceptually, quantum supremacy involves both the engineering task of building a powerful quantum computer and the computational-complexity-theoretic task of finding a problem that can be solved by that quantum computer and has a superpolynomial speedup over the best known or possible classical algorithm for that task. The term was coined by John Preskill in 2012, but the concept of a quantum computational advantage, specifically for simulating quantum systems, dates back to Yuri Manin's (1980) and Richard Feynman's (1981) proposals of quantum computing. Examples of proposals to demonstrate quantum supremacy include the boson sampling proposal of Aaronson and Arkhipov, D-Wave's specialized frustrated cluster loop problems, and sampling the output of random quantum circuits.
Aram Wettroth Harrow is an Associate Professor of Physics in the Massachusetts Institute of Technology's Center for Theoretical Physics.
Continuous-variable quantum information is the area of quantum information science that makes use of physical observables, like the strength of an electromagnetic field, whose numerical values belong to continuous intervals. One primary application is quantum computing. In a sense, continuous-variable quantum computation is "analog", while quantum computation using qubits is "digital." In more technical terms, the former makes use of Hilbert spaces that are infinite-dimensional, while the Hilbert spaces for systems comprising collections of qubits are finite-dimensional. One motivation for studying continuous-variable quantum computation is to understand what resources are necessary to make quantum computers more powerful than classical ones.
In quantum computing, a qubit is a unit of information analogous to a bit in classical computing, but it is affected by quantum mechanical properties such as superposition and entanglement which allow qubits to be in some ways more powerful than classical bits for some tasks. Qubits are used in quantum circuits and quantum algorithms composed of quantum logic gates to solve computational problems, where they are used for input/output and intermediate computations.
Hamiltonian simulation is a problem in quantum information science that attempts to find the computational complexity and quantum algorithms needed for simulating quantum systems. Hamiltonian simulation is a problem that demands algorithms which implement the evolution of a quantum state efficiently. The Hamiltonian simulation problem was proposed by Richard Feynman in 1982, where he proposed a quantum computer as a possible solution since the simulation of general Hamiltonians seem to grow exponentially with respect to the system size.
Applying classical methods of machine learning to the study of quantum systems is the focus of an emergent area of physics research. A basic example of this is quantum state tomography, where a quantum state is learned from measurement. Other examples include learning Hamiltonians, learning quantum phase transitions, and automatically generating new quantum experiments. Classical machine learning is effective at processing large amounts of experimental or calculated data in order to characterize an unknown quantum system, making its application useful in contexts including quantum information theory, quantum technologies development, and computational materials design. In this context, it can be used for example as a tool to interpolate pre-calculated interatomic potentials or directly solving the Schrödinger equation with a variational method.
References
- ↑ Lloyd, Seth (23 August 1996). "Universal Quantum Simulators". Science . American Association for the Advancement of Science. 273 (5278): 1073–1078. Bibcode:1996Sci...273.1073L. doi:10.1126/science.273.5278.1073. eISSN 1095-9203. ISSN 0036-8075. LCCN 17024346. OCLC 1644869. PMID 8688088.
- ↑ Sasaki, Masahide; Carlini, Alberto; Jozsa, Richard (17 July 2001). "Quantum template matching". Physical Review A . American Physical Society. 64 (2): 22317. arXiv: quant-ph/0102020 . Bibcode:2001PhRvA..64b2317S. doi:10.1103/PhysRevA.64.022317. eISSN 1094-1622. ISSN 1050-2947. OCLC 21266025.
- ↑ Gonzalez, Rafael C.; Woods, Richard E. (30 March 2017). Digital Image Processing (4th ed.). Pearson. ISBN 978-0133356724. OCLC 987436552.
- ↑ Yao, Xi-Wei; Wang, Hengyan; Liao, Zeyang; Chen, Ming-Cheng; Pan, Jian; et al. (11 September 2017). "Quantum Image Processing and Its Application to Edge Detection: Theory and Experiment". Physical Review X . American Physical Society. 7 (3): 31041. arXiv: 1801.01465 . Bibcode:2017PhRvX...7c1041Y. doi:10.1103/physrevx.7.031041. ISSN 2160-3308. LCCN 2011201149. OCLC 706478714.