In physics, the cross section is a measure of the probability that a specific process will take place in a collision of two particles. For example, the Rutherford cross-section is a measure of probability that an alpha particle will be deflected by a given angle during an interaction with an atomic nucleus. Cross section is typically denoted σ (sigma) and is expressed in units of area, more specifically in barns. In a way, it can be thought of as the size of the object that the excitation must hit in order for the process to occur, but more exactly, it is a parameter of a stochastic process.

Diffraction is the interference or bending of waves around the corners of an obstacle or through an aperture into the region of geometrical shadow of the obstacle/aperture. The diffracting object or aperture effectively becomes a secondary source of the propagating wave. Italian scientist Francesco Maria Grimaldi coined the word diffraction and was the first to record accurate observations of the phenomenon in 1660.

In mathematical physics and mathematics, the Pauli matrices are a set of three 2 × 2 complex matrices that are Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries.

In particle physics, bremsstrahlung is electromagnetic radiation produced by the deceleration of a charged particle when deflected by another charged particle, typically an electron by an atomic nucleus. The moving particle loses kinetic energy, which is converted into radiation, thus satisfying the law of conservation of energy. The term is also used to refer to the process of producing the radiation. Bremsstrahlung has a continuous spectrum, which becomes more intense and whose peak intensity shifts toward higher frequencies as the change of the energy of the decelerated particles increases.

X-ray photoelectron spectroscopy (XPS) is a surface-sensitive quantitative spectroscopic technique based on the photoelectric effect that can identify the elements that exist within a material or are covering its surface, as well as their chemical state, and the overall electronic structure and density of the electronic states in the material. XPS is a powerful measurement technique because it not only shows what elements are present, but also what other elements they are bonded to. The technique can be used in line profiling of the elemental composition across the surface, or in depth profiling when paired with ion-beam etching. It is often applied to study chemical processes in the materials in their as-received state or after cleavage, scraping, exposure to heat, reactive gasses or solutions, ultraviolet light, or during ion implantation.

In optics, a Fabry–Pérot interferometer (FPI) or etalon is an optical cavity made from two parallel reflecting surfaces. Optical waves can pass through the optical cavity only when they are in resonance with it. It is named after Charles Fabry and Alfred Perot, who developed the instrument in 1899. Etalon is from the French étalon, meaning "measuring gauge" or "standard".

Angular resolution describes the ability of any image-forming device such as an optical or radio telescope, a microscope, a camera, or an eye, to distinguish small details of an object, thereby making it a major determinant of image resolution. It is used in optics applied to light waves, in antenna theory applied to radio waves, and in acoustics applied to sound waves. The colloquial use of the term "resolution" sometimes causes confusion; when an optical system is said to have a high resolution or high angular resolution, it means that the perceived distance, or actual angular distance, between resolved neighboring objects is small. The value that quantifies this property, θ, which is given by the Rayleigh criterion, is low for a system with a high resolution. The closely related term spatial resolution refers to the precision of a measurement with respect to space, which is directly connected to angular resolution in imaging instruments. The Rayleigh criterion shows that the minimum angular spread that can be resolved by an image forming system is limited by diffraction to the ratio of the wavelength of the waves to the aperture width. For this reason, high resolution imaging systems such as astronomical telescopes, long distance telephoto camera lenses and radio telescopes have large apertures.
In many areas of science, Bragg's law, Wulff–Bragg's condition, or Laue–Bragg interference are a special case of Laue diffraction, giving the angles for coherent scattering of waves from a large crystal lattice. It describes how the superposition of wave fronts scattered by lattice planes leads to a strict relation between the wavelength and scattering angle. This law was initially formulated for X-rays, but it also applies to all types of matter waves including neutron and electron waves if there are a large number of atoms, as well as visible light with artificial periodic microscale lattices.
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when plane waves are incident on a diffracting object, and the diffraction pattern is viewed at a sufficiently long distance from the object, and also when it is viewed at the focal plane of an imaging lens. In contrast, the diffraction pattern created near the diffracting object and is given by the Fresnel diffraction equation.
In quantum physics, the scattering amplitude is the probability amplitude of the outgoing spherical wave relative to the incoming plane wave in a stationary-state scattering process. At large distances from the centrally symmetric scattering center, the plane wave is described by the wavefunction
Rietveld refinement is a technique described by Hugo Rietveld for use in the characterisation of crystalline materials. The neutron and X-ray diffraction of powder samples results in a pattern characterised by reflections at certain positions. The height, width and position of these reflections can be used to determine many aspects of the material's structure.
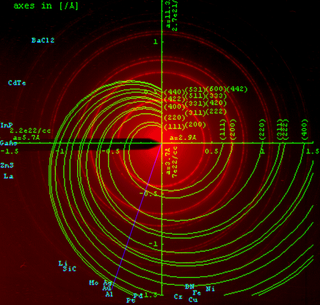
Powder diffraction is a scientific technique using X-ray, neutron, or electron diffraction on powder or microcrystalline samples for structural characterization of materials. An instrument dedicated to performing such powder measurements is called a powder diffractometer.
Angular distance or angular separation is the measure of the angle between the orientation of two straight lines, rays, or vectors in three-dimensional space, or the central angle subtended by the radii through two points on a sphere. When the rays are lines of sight from an observer to two points in space, it is known as the apparent distance or apparent separation.
Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. An individual photon can be described as having right or left circular polarization, or a superposition of the two. Equivalently, a photon can be described as having horizontal or vertical linear polarization, or a superposition of the two.

In optics, a dispersive prism is an optical prism that is used to disperse light, that is, to separate light into its spectral components. Different wavelengths (colors) of light will be deflected by the prism at different angles. This is a result of the prism material's index of refraction varying with wavelength (dispersion). Generally, longer wavelengths (red) undergo a smaller deviation than shorter wavelengths (blue). The dispersion of white light into colors by a prism led Sir Isaac Newton to conclude that white light consisted of a mixture of different colors.
The Scherrer equation, in X-ray diffraction and crystallography, is a formula that relates the size of sub-micrometre crystallites in a solid to the broadening of a peak in a diffraction pattern. It is often referred to, incorrectly, as a formula for particle size measurement or analysis. It is named after Paul Scherrer. It is used in the determination of size of crystals in the form of powder.
Surface-extended X-ray absorption fine structure (SEXAFS) is the surface-sensitive equivalent of the EXAFS technique. This technique involves the illumination of the sample by high-intensity X-ray beams from a synchrotron and monitoring their photoabsorption by detecting in the intensity of Auger electrons as a function of the incident photon energy. Surface sensitivity is achieved by the interpretation of data depending on the intensity of the Auger electrons instead of looking at the relative absorption of the X-rays as in the parent method, EXAFS.

The contrast transfer function (CTF) mathematically describes how aberrations in a transmission electron microscope (TEM) modify the image of a sample. This contrast transfer function (CTF) sets the resolution of high-resolution transmission electron microscopy (HRTEM), also known as phase contrast TEM.
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens.





























