Related Research Articles

An algebraic number is a number that is a root of a non-zero polynomial in one variable with integer coefficients. For example, the golden ratio, , is an algebraic number, because it is a root of the polynomial x2 − x − 1. That is, it is a value for x for which the polynomial evaluates to zero. As another example, the complex number is algebraic because it is a root of x4 + 4.

The Ulam spiral or prime spiral is a graphical depiction of the set of prime numbers, devised by mathematician Stanisław Ulam in 1963 and popularized in Martin Gardner's Mathematical Games column in Scientific American a short time later. It is constructed by writing the positive integers in a square spiral and specially marking the prime numbers.
In mathematics, a quadratic form is a polynomial with terms all of degree two. For example,

Lagrange's four-square theorem, also known as Bachet's conjecture, states that every nonnegative integer can be represented as a sum of four non-negative integer squares. That is, the squares form an additive basis of order four. where the four numbers are integers. For illustration, 3, 31, and 310 can be represented as the sum of four squares as follows:
29 (twenty-nine) is the natural number following 28 and preceding 30. It is a prime number.
71 (seventy-one) is the natural number following 70 and preceding 72.
In mathematics, the Birch and Swinnerton-Dyer conjecture describes the set of rational solutions to equations defining an elliptic curve. It is an open problem in the field of number theory and is widely recognized as one of the most challenging mathematical problems. It is named after mathematicians Bryan John Birch and Peter Swinnerton-Dyer, who developed the conjecture during the first half of the 1960s with the help of machine computation. Only special cases of the conjecture have been proven.

A powerful number is a positive integer m such that for every prime number p dividing m, p2 also divides m. Equivalently, a powerful number is the product of a square and a cube, that is, a number m of the form m = a2b3, where a and b are positive integers. Powerful numbers are also known as squareful, square-full, or 2-full. Paul Erdős and George Szekeres studied such numbers and Solomon W. Golomb named such numbers powerful.
In mathematics, Helmut Hasse's local–global principle, also known as the Hasse principle, is the idea that one can find an integer solution to an equation by using the Chinese remainder theorem to piece together solutions modulo powers of each different prime number. This is handled by examining the equation in the completions of the rational numbers: the real numbers and the p-adic numbers. A more formal version of the Hasse principle states that certain types of equations have a rational solution if and only if they have a solution in the real numbers and in the p-adic numbers for each prime p.
2000 is a natural number following 1999 and preceding 2001.
1729 is the natural number following 1728 and preceding 1730. It is the first nontrivial taxicab number, expressed as the sum of two cubic numbers in two different ways. It is known as the Ramanujan number or Hardy–Ramanujan number after G. H. Hardy and Srinivasa Ramanujan.
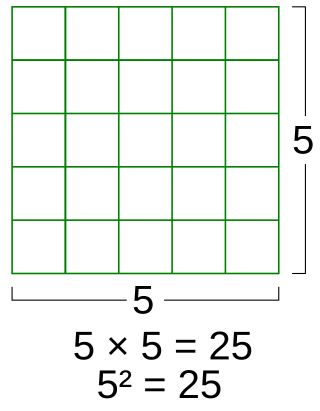
In mathematics, a square is the result of multiplying a number by itself. The verb "to square" is used to denote this operation. Squaring is the same as raising to the power 2, and is denoted by a superscript 2; for instance, the square of 3 may be written as 32, which is the number 9. In some cases when superscripts are not available, as for instance in programming languages or plain text files, the notations x^2 (caret) or x**2 may be used in place of x2. The adjective which corresponds to squaring is quadratic.
In mathematics, the 15 theorem or Conway–Schneeberger Fifteen Theorem, proved by John H. Conway and W. A. Schneeberger in 1993, states that if a positive definite quadratic form with integer matrix represents all positive integers up to 15, then it represents all positive integers. The proof was complicated, and was never published. Manjul Bhargava found a much simpler proof which was published in 2000.
In mathematics, a universal quadratic form is a quadratic form over a ring that represents every element of the ring. A non-singular form over a field which represents zero non-trivially is universal.

Ken Ono is an American mathematician with fields of study in number theory. He is the STEM Advisor to the Provost and the Marvin Rosenblum Professor of Mathematics at the University of Virginia.
Brocard's problem is a problem in mathematics that seeks integer values of such that is a perfect square, where is the factorial. Only three values of are known — 4, 5, 7 — and it is not known whether there are any more.
In mathematics, the Hardy–Ramanujan theorem, proved by Ramanujan and checked by Hardy states that the normal order of the number of distinct prime factors of a number is .
In mathematics, specifically the field of transcendental number theory, the four exponentials conjecture is a conjecture which, given the right conditions on the exponents, would guarantee the transcendence of at least one of four exponentials. The conjecture, along with two related, stronger conjectures, is at the top of a hierarchy of conjectures and theorems concerning the arithmetic nature of a certain number of values of the exponential function.
A Proth number is a natural number N of the form where k and n are positive integers, k is odd and . A Proth prime is a Proth number that is prime. They are named after the French mathematician François Proth. The first few Proth primes are
References
- 1 2 3 4 Ono, Ken; Soundararajan, Kannan (1997). "Ramanujan's ternary quadratic form" (PDF). Inventiones Mathematicae . 130 (3): 415–454. Bibcode:1997InMat.130..415O. CiteSeerX 10.1.1.585.8840 . doi:10.1007/s002220050191. MR 1483991. S2CID 122314044.
- 1 2 Jones, Burton W.; Pall, Gordon (1939). "Regular and semi-regular positive ternary quadratic forms". Acta Mathematica . 70 (1): 165–191. doi: 10.1007/bf02547347 . MR 1555447.
- 1 2 3 Ramanujan, S. (1916). "On the expression of a number in the form ax2 + by2 + cz2 + du2". Mathematical Proceedings of the Cambridge Philosophical Society . 19: 11–21.
- ↑ Gupta, Hansraj (1941). "Some idiosyncratic numbers of Ramanujan" (PDF). Proceedings of the Indian Academy of Sciences, Section A. 13 (6): 519–520. doi:10.1007/BF03049015. MR 0004816. S2CID 116006923.
- ↑ L. E. Dickson (1926–1927). "Ternary Quadratic Forms and Congruences". Annals of Mathematics. Second Series. 28 (1/4): 333–341. doi:10.2307/1968378. JSTOR 1968378. MR 1502786.