Examples
A sample graph and matrix:
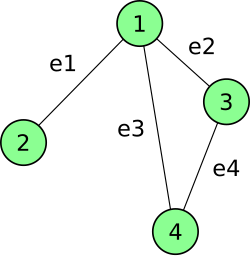
(corresponding to the four edges, e1–e4):
| = |
In this example, the matrix theory rank of the matrix is 4, because its column vectors are linearly independent.
| Relevant topics on |
| Graph connectivity |
|---|
In graph theory, a branch of mathematics, the rank of an undirected graph has two unrelated definitions. Let n equal the number of vertices of the graph.
A sample graph and matrix:

(corresponding to the four edges, e1–e4):
| = |
In this example, the matrix theory rank of the matrix is 4, because its column vectors are linearly independent.

In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices which are connected by edges. A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics.
In combinatorics, a branch of mathematics, a matroid is a structure that abstracts and generalizes the notion of linear independence in vector spaces. There are many equivalent ways to define a matroid axiomatically, the most significant being in terms of: independent sets; bases or circuits; rank functions; closure operators; and closed sets or flats. In the language of partially ordered sets, a finite simple matroid is equivalent to a geometric lattice.
In graph theory and computer science, an adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph.

In graph theory, a component of an undirected graph is a connected subgraph that is not part of any larger connected subgraph. The components of any graph partition its vertices into disjoint sets, and are the induced subgraphs of those sets. A graph that is itself connected has exactly one component, consisting of the whole graph. Components are sometimes called connected components.
In graph theory, a branch of mathematics, the (binary) cycle space of an undirected graph is the set of its even-degree subgraphs.

In discrete mathematics, and more specifically in graph theory, a graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense "related". The objects are represented by abstractions called vertices and each of the related pairs of vertices is called an edge. Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges.
In mathematics, an incidence matrix is a logical matrix that shows the relationship between two classes of objects, usually called an incidence relation. If the first class is X and the second is Y, the matrix has one row for each element of X and one column for each element of Y. The entry in row x and column y is 1 if x and y are related and 0 if they are not. There are variations; see below.
In computer science, a graph is an abstract data type that is meant to implement the undirected graph and directed graph concepts from the field of graph theory within mathematics.
In mathematics, a unimodular matrixM is a square integer matrix having determinant +1 or −1. Equivalently, it is an integer matrix that is invertible over the integers: there is an integer matrix N that is its inverse. Thus every equation Mx = b, where M and b both have integer components and M is unimodular, has an integer solution. The n × n unimodular matrices form a group called the n × n general linear group over , which is denoted .
In the mathematical field of graph theory, Kirchhoff's theorem or Kirchhoff's matrix tree theorem named after Gustav Kirchhoff is a theorem about the number of spanning trees in a graph, showing that this number can be computed in polynomial time from the determinant of a submatrix of the Laplacian matrix of the graph; specifically, the number is equal to any cofactor of the Laplacian matrix. Kirchhoff's theorem is a generalization of Cayley's formula which provides the number of spanning trees in a complete graph.
In the mathematical field of graph theory, the Laplacian matrix, also called the graph Laplacian, admittance matrix, Kirchhoff matrix or discrete Laplacian, is a matrix representation of a graph. Named after Pierre-Simon Laplace, the graph Laplacian matrix can be viewed as a matrix form of the negative discrete Laplace operator on a graph approximating the negative continuous Laplacian obtained by the finite difference method.
In the mathematical field of algebraic graph theory, the degree matrix of an undirected graph is a diagonal matrix which contains information about the degree of each vertex—that is, the number of edges attached to each vertex. It is used together with the adjacency matrix to construct the Laplacian matrix of a graph: the Laplacian matrix is the difference of the degree matrix and the adjacency matrix.

In graph theory, a branch of mathematics, the circuit rank, cyclomatic number, cycle rank, or nullity of an undirected graph is the minimum number of edges that must be removed from the graph to break all its cycles, making it into a tree or forest. It is equal to the number of independent cycles in the graph. Unlike the corresponding feedback arc set problem for directed graphs, the circuit rank r is easily computed using the formula
A logical matrix, binary matrix, relation matrix, Boolean matrix, or (0, 1)-matrix is a matrix with entries from the Boolean domain B = {0, 1}. Such a matrix can be used to represent a binary relation between a pair of finite sets. It is an important tool in combinatorial mathematics and theoretical computer science.
The nullity of a graph in the mathematical subject of graph theory can mean either of two unrelated numbers. If the graph has n vertices and m edges, then:

In mathematics, and more specifically in graph theory, a directed graph is a graph that is made up of a set of vertices connected by directed edges, often called arcs.
In the mathematical theory of matroids, the rank of a matroid is the maximum size of an independent set in the matroid. The rank of a subset S of elements of the matroid is, similarly, the maximum size of an independent subset of S, and the rank function of the matroid maps sets of elements to their ranks.
In the mathematical theory of matroids, a matroid representation is a family of vectors whose linear independence relation is the same as that of a given matroid. Matroid representations are analogous to group representations; both types of representation provide abstract algebraic structures with concrete descriptions in terms of linear algebra.
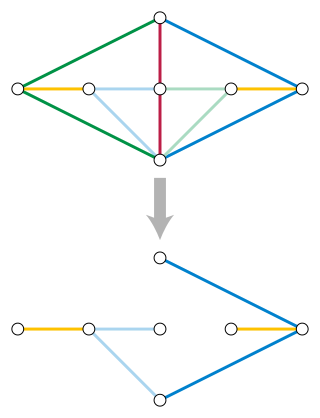
In combinatorial optimization, the matroid parity problem is a problem of finding the largest independent set of paired elements in a matroid. The problem was formulated by Lawler (1976) as a common generalization of graph matching and matroid intersection. It is also known as polymatroid matching, or the matchoid problem.