In electrodynamics, elliptical polarization is the polarization of electromagnetic radiation such that the tip of the electric field vector describes an ellipse in any fixed plane intersecting, and normal to, the direction of propagation. An elliptically polarized wave may be resolved into two linearly polarized waves in phase quadrature, with their polarization planes at right angles to each other. Since the electric field can rotate clockwise or counterclockwise as it propagates, elliptically polarized waves exhibit chirality.

In crystallography, crystal structure is a description of the ordered arrangement of atoms, ions or molecules in a crystalline material. Ordered structures occur from the intrinsic nature of the constituent particles to form symmetric patterns that repeat along the principal directions of three-dimensional space in matter.
In electromagnetics, an evanescent field, or evanescent wave, is an oscillating electric and/or magnetic field that does not propagate as an electromagnetic wave but whose energy is spatially concentrated in the vicinity of the source. Even when there is a propagating electromagnetic wave produced, one can still identify as an evanescent field the component of the electric or magnetic field that cannot be attributed to the propagating wave observed at a distance of many wavelengths.
In classical and quantum mechanics, geometric phase is a phase difference acquired over the course of a cycle, when a system is subjected to cyclic adiabatic processes, which results from the geometrical properties of the parameter space of the Hamiltonian. The phenomenon was independently discovered by T. Kato (1950), S. Pancharatnam (1956), and by H. C. Longuet-Higgins (1958) and later generalized by Sir Michael Berry (1984). It is also known as the Pancharatnam–Berry phase, Pancharatnam phase, or Berry phase. It can be seen in the conical intersection of potential energy surfaces and in the Aharonov–Bohm effect. Geometric phase around the conical intersection involving the ground electronic state of the C6H3F3+ molecular ion is discussed on pages 385-386 of the textbook by Bunker and Jensen. In the case of the Aharonov–Bohm effect, the adiabatic parameter is the magnetic field enclosed by two interference paths, and it is cyclic in the sense that these two paths form a loop. In the case of the conical intersection, the adiabatic parameters are the molecular coordinates. Apart from quantum mechanics, it arises in a variety of other wave systems, such as classical optics. As a rule of thumb, it can occur whenever there are at least two parameters characterizing a wave in the vicinity of some sort of singularity or hole in the topology; two parameters are required because either the set of nonsingular states will not be simply connected, or there will be nonzero holonomy.
In physics, a ferromagnetic material is said to have magnetocrystalline anisotropy if it takes more energy to magnetize it in certain directions than in others. These directions are usually related to the principal axes of its crystal lattice. It is a special case of magnetic anisotropy.

A polaron is a quasiparticle used in condensed matter physics to understand the interactions between electrons and atoms in a solid material. The polaron concept was proposed by Lev Landau in 1933 and Solomon Pekar in 1946 to describe an electron moving in a dielectric crystal where the atoms displace from their equilibrium positions to effectively screen the charge of an electron, known as a phonon cloud. For comparison of the models proposed in these papers see M. I. Dykman and E. I. Rashba, The roots of polaron theory, Physics Today 68, 10 (2015). This lowers the electron mobility and increases the electron's effective mass.
In general relativity, the Gibbons–Hawking–York boundary term is a term that needs to be added to the Einstein–Hilbert action when the underlying spacetime manifold has a boundary.

A lattice constant or lattice parameter is one of the physical dimensions and angles that determine the geometry of the unit cells in a crystal lattice. Lattices in three dimensions generally have six lattice constants: the lengths a, b, and c of the three cell edges meeting at a vertex, and the angles α, β, and γ between those edges.

In physics the magneto-optic Kerr effect (MOKE) or the surface magneto-optic Kerr effect (SMOKE) is one of the magneto-optic effects. It describes the changes to light reflected from a magnetized surface. It is used in materials science research in devices such as the Kerr microscope, to investigate the magnetization structure of materials.
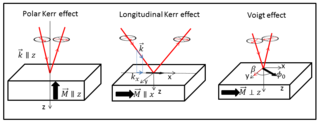
The Voigt effect is a magneto-optical phenomenon which rotates and elliptizes linearly polarised light sent into an optically active medium. Unlike many other magneto-optical effects such as the Kerr or Faraday effect which are linearly proportional to the magnetization, the Voigt effect is proportional to the square of the magnetization and can be seen experimentally at normal incidence. There are several denominations for this effect in the literature: the Cotton–Mouton effect, the Voigt effect, and magnetic-linear birefringence. This last denomination is closer in the physical sense, where the Voigt effect is a magnetic birefringence of the material with an index of refraction parallel and perpendicular ) to the magnetization vector or to the applied magnetic field.
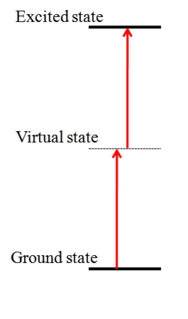
Two-photon absorption or two-photon excitation or non-linear absorption is the simultaneous absorption of two photons of identical or different frequencies in order to excite a molecule from one state to a higher energy, most commonly an excited electronic state. Absorption of two photons with different frequencies is called non-degenerate two-photon absorption. Since TPA depends on the simultaneous absorption of two photons, the probability of TPA is proportional to the square of the light intensity, thus it is a nonlinear optical process. The energy difference between the involved lower and upper states of the molecule is equal or smaller than the sum of the photon energies of the two photons absorbed. Two-photon absorption is a third-order process, with absorption cross section typically several orders of magnitude smaller than one-photon absorption cross section.
Diffuse reflectance spectroscopy, or diffuse reflection spectroscopy, is a subset of absorption spectroscopy. It is sometimes called remission spectroscopy. Remission is the reflection or back-scattering of light by a material, while transmission is the passage of light through a material. The word remission implies a direction of scatter, independent of the scattering process. Remission includes both specular and diffusely back-scattered light. The word reflection often implies a particular physical process, such as specular reflection.
The Sudarshan-Glauber P representation is a suggested way of writing down the phase space distribution of a quantum system in the phase space formulation of quantum mechanics. The P representation is the quasiprobability distribution in which observables are expressed in normal order. In quantum optics, this representation, formally equivalent to several other representations, is sometimes championed over alternative representations to describe light in optical phase space, because typical optical observables, such as the particle number operator, are naturally expressed in normal order. It is named after George Sudarshan and Roy J. Glauber, who worked on the topic in 1963. Despite many useful applications in laser theory and coherence theory, the Glauber–Sudarshan P representation has the drawback that it is not always positive, and is not a true probability function.
In condensed matter physics, magnetic anisotropy describes how an object's magnetic properties can be different depending on direction. In the simplest case, there is no preferential direction for an object's magnetic moment. It will respond to an applied magnetic field in the same way, regardless of which direction the field is applied. This is known as magnetic isotropy. In contrast, magnetically anisotropic materials will be easier or harder to magnetize depending on which way the object is rotated.
Originally, the Preisach model of hysteresis generalized magnetic hysteresis as the relationship between the magnetic field and magnetization of a magnetic material as the parallel connection of independent relay hysterons. It was first suggested in 1935 by Ferenc (Franz) Preisach in the German academic journal Zeitschrift für Physik. In the field of ferromagnetism, the Preisach model is sometimes thought to describe a ferromagnetic material as a network of small independently acting domains, each magnetized to a value of either or . A sample of iron, for example, may have evenly distributed magnetic domains, resulting in a net magnetic moment of zero.

In solid state physics, a surface phonon is the quantum of a lattice vibration mode associated with a solid surface. Similar to the ordinary lattice vibrations in a bulk solid, the nature of surface vibrations depends on details of periodicity and symmetry of a crystal structure. Surface vibrations are however distinct from the bulk vibrations, as they arise from the abrupt termination of a crystal structure at the surface of a solid. Knowledge of surface phonon dispersion gives important information related to the amount of surface relaxation, the existence and distance between an adsorbate and the surface, and information regarding presence, quantity, and type of defects existing on the surface.
In its most general form, the magnetoelectric effect (ME) denotes any coupling between the magnetic and the electric properties of a material. The first example of such an effect was described by Wilhelm Röntgen in 1888, who found that a dielectric material moving through an electric field would become magnetized. A material where such a coupling is intrinsically present is called a magnetoelectric.

In theoretical physics, Lovelock's theory of gravity is a generalization of Einstein's theory of general relativity introduced by David Lovelock in 1971. It is the most general metric theory of gravity yielding conserved second order equations of motion in an arbitrary number of spacetime dimensions D. In this sense, Lovelock's theory is the natural generalization of Einstein's General Relativity to higher dimensions. In three and four dimensions, Lovelock's theory coincides with Einstein's theory, but in higher dimensions the theories are different. In fact, for D > 4 Einstein gravity can be thought of as a particular case of Lovelock gravity since the Einstein–Hilbert action is one of several terms that constitute the Lovelock action.

A phonovoltaic (pV) cell converts vibrational (phonons) energy into a direct current much like the photovoltaic effect in a photovoltaic (PV) cell converts light (photon) into power. That is, it uses a p-n junction to separate the electrons and holes generated as valence electrons absorb optical phonons more energetic than the band gap, and then collects them in the metallic contacts for use in a circuit. The pV cell is an application of heat transfer physics and competes with other thermal energy harvesting devices like the thermoelectric generator.

In theoretical physics, the dual graviton is a hypothetical elementary particle that is a dual of the graviton under electric-magnetic duality, as an S-duality, predicted by some formulations of supergravity in eleven dimensions.












