As a topic of economics, utility is used to model worth or value. Its usage has evolved significantly over time. The term was introduced initially as a measure of pleasure or happiness as part of the theory of utilitarianism by moral philosophers such as Jeremy Bentham and John Stuart Mill. The term has been adapted and reapplied within neoclassical economics, which dominates modern economic theory, as a utility function that represents a single consumer's preference ordering over a choice set but is not comparable across consumers. This concept of utility is personal and based on choice rather than on pleasure received, and so is specified more rigorously than the original concept but makes it less useful for ethical decisions.

In mathematics, especially in order theory, a maximal element of a subset S of some preordered set is an element of S that is not smaller than any other element in S. A minimal element of a subset S of some preordered set is defined dually as an element of S that is not greater than any other element in S.
In economics, an ordinal utility function is a function representing the preferences of an agent on an ordinal scale. Ordinal utility theory claims that it is only meaningful to ask which option is better than the other, but it is meaningless to ask how much better it is or how good it is. All of the theory of consumer decision-making under conditions of certainty can be, and typically is, expressed in terms of ordinal utility.
Revealed preference theory, pioneered by economist Paul Anthony Samuelson in 1938, is a method of analyzing choices made by individuals, mostly used for comparing the influence of policies on consumer behavior. Revealed preference models assume that the preferences of consumers can be revealed by their purchasing habits.
In economics, convex preferences are an individual's ordering of various outcomes, typically with regard to the amounts of various goods consumed, with the property that, roughly speaking, "averages are better than the extremes". The concept roughly corresponds to the concept of diminishing marginal utility without requiring utility functions.
Competitive equilibrium is a concept of economic equilibrium introduced by Kenneth Arrow and Gérard Debreu in 1951 appropriate for the analysis of commodity markets with flexible prices and many traders, and serving as the benchmark of efficiency in economic analysis. It relies crucially on the assumption of a competitive environment where each trader decides upon a quantity that is so small compared to the total quantity traded in the market that their individual transactions have no influence on the prices. Competitive markets are an ideal standard by which other market structures are evaluated.
In probability theory and statistics, a stochastic order quantifies the concept of one random variable being "bigger" than another. These are usually partial orders, so that one random variable may be neither stochastically greater than, less than nor equal to another random variable . Many different orders exist, which have different applications.
In decision theory, the von Neumann–Morgenstern (VNM) utility theorem shows that, under certain axioms of rational behavior, a decision-maker faced with risky (probabilistic) outcomes of different choices will behave as if he or she is maximizing the expected value of some function defined over the potential outcomes at some specified point in the future. This function is known as the von Neumann–Morgenstern utility function. The theorem is the basis for expected utility theory.
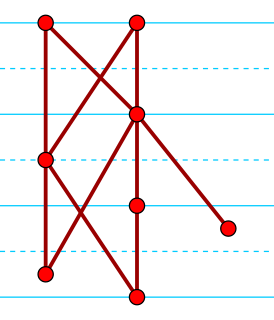
In order theory, a branch of mathematics, a semiorder is a type of ordering for items with numerical scores, where items with widely differing scores are compared by their scores and where scores within a given margin of error are deemed incomparable. Semiorders were introduced and applied in mathematical psychology by Duncan Luce (1956) as a model of human preference. They generalize strict weak orderings, in which items with equal scores may be tied but there is no margin of error. They are a special case of partial orders and of interval orders, and can be characterized among the partial orders by additional axioms, or by two forbidden four-item suborders.
Some branches of economics and game theory deal with indivisible goods, discrete items that can be traded only as a whole. For example, in combinatorial auctions there is a finite set of items, and every agent can buy a subset of the items, but an item cannot be divided among two or more agents.
Fair item allocation is a kind of a fair division problem in which the items to divide are discrete rather than continuous. The items have to be divided among several partners who value them differently, and each item has to be given as a whole to a single person. This situation arises in various real-life scenarios:
In economics, the Debreu theorems are several statements about the representation of a preference ordering by a real-valued function. The theorems were proved by Gerard Debreu during the 1950s.
In decision theory, a multi-attribute utility function is used to represent the preferences of an agent over bundles of goods either under conditions of certainty about the results of any potential choice, or under conditions of uncertainty.
Envy-freeness, also known as no-envy, is a criterion for fair division. It says that, when resources are allocated among people with equal rights, each person should receive a share that is, in their eyes, at least as good as the share received by any other agent. In other words, no person should feel envy.
In economics, the overtaking criterion is used to compare infinite streams of outcomes. Mathematically, it is used to properly define a notion of optimality for a problem of optimal control on an unbounded time interval.
In economics, gross substitutes (GS) is a class of utility functions on indivisible goods. An agent is said to have a GS valuation if, whenever the prices of some items increase and the prices of other items remain constant, the agent's demand for the items whose price remain constant weakly increases.
Envy-free (EF) item allocation is a fair item allocation problem, in which the fairness criterion is envy-freeness - each agent should receive a bundle that they believe to be at least as good as the bundle of any other agent.
In theoretical economics, an abstract economy is a model that generalizes both the standard model of an exchange economy in microeconomics, and the standard model of a game in game theory. An equilibrium in an abstract economy generalizes both a Walrasian equilibrium in microeconomics, and a Nash equilibrium in game-theory.
Finitist set theory (FST) is a collection theory designed for modeling finite nested structures of individuals and a variety of transitive and antitransitive chains of relations between individuals. Unlike classical set theories such as ZFC and KPU, FST is not intended to function as a foundation for mathematics, but only as a tool in ontological modeling. FST functions as the logical foundation of the classical layer-cake interpretation, and manages to incorporate a large portion of the functionality of discrete mereology.
The finite promise games are a collection of mathematical games developed by American mathematician Harvey Friedman in 2009 which are used to develop a family of fast-growing functions , and . The greedy clique sequence is a graph theory concept, also developed by Friedman in 2010, which are used to develop fast-growing functions , and .



















































