In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force F proportional to the displacement x:

Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples of oscillation include a swinging pendulum and alternating current. Oscillations can be used in physics to approximate complex interactions, such as those between atoms.
In mechanics and physics, simple harmonic motion is a special type of periodic motion where the restoring force on the moving object is directly proportional to the magnitude of the object's displacement and acts towards the object's equilibrium position. It results in an oscillation which continues indefinitely, if uninhibited by friction or any other dissipation of energy.

The (two-way) wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields — as they occur in classical physics — such as mechanical waves or electromagnetic waves. It arises in fields like acoustics, electromagnetism, and fluid dynamics. A single wave propagating in a pre-defined direction can also be described with the one-way wave equation.
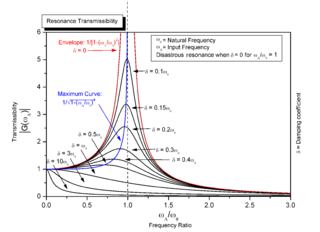
Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied periodic force is equal or close to a natural frequency of the system on which it acts. When an oscillating force is applied at a resonant frequency of a dynamic system, the system will oscillate at a higher amplitude than when the same force is applied at other, non-resonant frequencies.

The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary smooth potential can usually be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics. Furthermore, it is one of the few quantum-mechanical systems for which an exact, analytical solution is known.
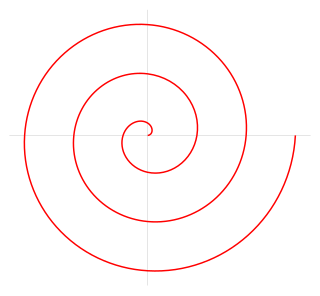
The Archimedean spiral is a spiral named after the 3rd-century BC Greek mathematician Archimedes. It is the locus corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line that rotates with constant angular velocity. Equivalently, in polar coordinates (r, θ) it can be described by the equation
Kinematics is a subfield of physics, developed in classical mechanics, that describes the motion of points, bodies (objects), and systems of bodies without considering the forces that cause them to move. Kinematics, as a field of study, is often referred to as the "geometry of motion" and is occasionally seen as a branch of mathematics. A kinematics problem begins by describing the geometry of the system and declaring the initial conditions of any known values of position, velocity and/or acceleration of points within the system. Then, using arguments from geometry, the position, velocity and acceleration of any unknown parts of the system can be determined. The study of how forces act on bodies falls within kinetics, not kinematics. For further details, see analytical dynamics.

A tautochrone or isochrone curve is the curve for which the time taken by an object sliding without friction in uniform gravity to its lowest point is independent of its starting point on the curve. The curve is a cycloid, and the time is equal to π times the square root of the radius over the acceleration of gravity. The tautochrone curve is related to the brachistochrone curve, which is also a cycloid.

An inverted pendulum is a pendulum that has its center of mass above its pivot point. It is unstable and without additional help will fall over. It can be suspended stably in this inverted position by using a control system to monitor the angle of the pole and move the pivot point horizontally back under the center of mass when it starts to fall over, keeping it balanced. The inverted pendulum is a classic problem in dynamics and control theory and is used as a benchmark for testing control strategies. It is often implemented with the pivot point mounted on a cart that can move horizontally under control of an electronic servo system as shown in the photo; this is called a cart and pole apparatus. Most applications limit the pendulum to 1 degree of freedom by affixing the pole to an axis of rotation. Whereas a normal pendulum is stable when hanging downwards, an inverted pendulum is inherently unstable, and must be actively balanced in order to remain upright; this can be done either by applying a torque at the pivot point, by moving the pivot point horizontally as part of a feedback system, changing the rate of rotation of a mass mounted on the pendulum on an axis parallel to the pivot axis and thereby generating a net torque on the pendulum, or by oscillating the pivot point vertically. A simple demonstration of moving the pivot point in a feedback system is achieved by balancing an upturned broomstick on the end of one's finger.

A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The free motion described by the normal modes takes place at fixed frequencies. These fixed frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies. A physical object, such as a building, bridge, or molecule, has a set of normal modes and their natural frequencies that depend on its structure, materials and boundary conditions. In music, normal modes of vibrating instruments are called "harmonics" or "overtones".

In relativity, proper time along a timelike world line is defined as the time as measured by a clock following that line. It is thus independent of coordinates, and is a Lorentz scalar. The proper time interval between two events on a world line is the change in proper time. This interval is the quantity of interest, since proper time itself is fixed only up to an arbitrary additive constant, namely the setting of the clock at some event along the world line.

The Wheeler–DeWitt equation for theoretical physics and applied mathematics, is a field equation attributed to John Archibald Wheeler and Bryce DeWitt. The equation attempts to mathematically combine the ideas of quantum mechanics and general relativity, a step towards a theory of quantum gravity.
In mathematics, constraint counting is counting the number of constraints in order to compare it with the number of variables, parameters, etc. that are free to be determined, the idea being that in most cases the number of independent choices that can be made is the excess of the latter over the former.
The reciprocating motion of a non-offset piston connected to a rotating crank through a connecting rod can be expressed by equations of motion. This article shows how these equations of motion can be derived using calculus as functions of angle (angle domain) and of time (time domain).

A pendulum is a body suspended from a fixed support so that it swings freely back and forth under the influence of gravity. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position. When released, the restoring force acting on the pendulum's mass causes it to oscillate about the equilibrium position, swinging it back and forth. The mathematics of pendulums are in general quite complicated. Simplifying assumptions can be made, which in the case of a simple pendulum allow the equations of motion to be solved analytically for small-angle oscillations.
A mechanical system is scleronomous if the equations of constraints do not contain the time as an explicit variable and the equation of constraints can be described by generalized coordinates. Such constraints are called scleronomic constraints. The opposite of scleronomous is rheonomous.
In classical mechanics, holonomic constraints are relations between the position variables that can be expressed in the following form:

Kapitza's pendulum or Kapitza pendulum is a rigid pendulum in which the pivot point vibrates in a vertical direction, up and down. It is named after Russian Nobel laureate physicist Pyotr Kapitza, who in 1951 developed a theory which successfully explains some of its unusual properties. The unique feature of the Kapitza pendulum is that the vibrating suspension can cause it to balance stably in an inverted position, with the bob above the suspension point. In the usual pendulum with a fixed suspension, the only stable equilibrium position is with the bob hanging below the suspension point; the inverted position is a point of unstable equilibrium, and the smallest perturbation moves the pendulum out of equilibrium. In nonlinear control theory the Kapitza pendulum is used as an example of a parametric oscillator that demonstrates the concept of "dynamic stabilization".
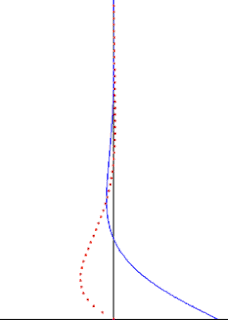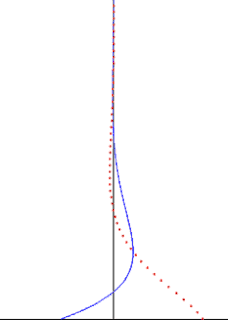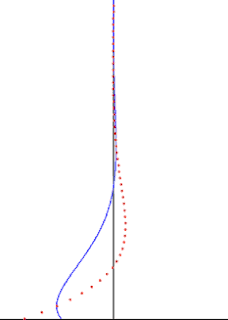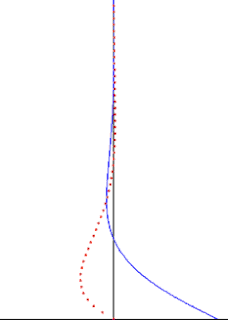
In fluid dynamics, Stokes problem also known as Stokes second problem or sometimes referred to as Stokes boundary layer or Oscillating boundary layer is a problem of determining the flow created by an oscillating solid surface, named after Sir George Stokes. This is considered one of the simplest unsteady problem that have exact solution for the Navier-Stokes equations. In turbulent flow, this is still named a Stokes boundary layer, but now one has to rely on experiments, numerical simulations or approximate methods in order to obtain useful information on the flow.





















