Richard Arratia

Last updated

Richard Alejandro Arratia is a mathematician noted for his work in combinatorics and probability theory.

Contents

Contributions

Arratia developed the ideas of interlace polynomials with Béla Bollobás and Gregory Sorkin, [paper 1] found an equivalent formulation of the Stanley–Wilf conjecture as the convergence of a limit, [paper 2] and was the first to investigate the lengths of superpatterns of permutations. [paper 2]

He has also written highly cited papers on the Chen–Stein method on distances between probability distributions, [paper 3] [paper 4] on random walks with exclusion, [paper 5] and on sequence alignment. [paper 6] [paper 7]

He is a coauthor of the book Logarithmic Combinatorial Structures: A Probabilistic Approach. [book 1] [1] [2]

Education and employment

Arratia earned his Ph.D. in 1979 from the University of Wisconsin–Madison under the supervision of David Griffeath. [3] He is currently a professor of mathematics at the University of Southern California. [4]

Selected publications

Research papers
  1. ↑ Arratia, Richard; Bollobás, Béla; Sorkin, Gregory B. (2004), "The interlace polynomial of a graph", Journal of Combinatorial Theory , Series B, 92 (2): 199–233, arXiv: math/0209045 , doi:10.1016/j.jctb.2004.03.003, MR   2099142, S2CID   6421047 .
  2. 1 2 Arratia, Richard (1999), "On the Stanley-Wilf conjecture for the number of permutations avoiding a given pattern", Electronic Journal of Combinatorics , 6, N1, doi: 10.37236/1477 , MR   1710623
  3. ↑ Arratia, R.; Goldstein, L.; Gordon, L. (1989), "Two moments suffice for Poisson approximations: the Chen–Stein method" (PDF), Annals of Probability , 17 (1): 9–25, doi: 10.1214/aop/1176991491 , JSTOR   2244193, MR   0972770 .
  4. ↑ Arratia, Richard; Goldstein, Larry; Gordon, Louis (1990), "Poisson approximation and the Chen–Stein method", Statistical Science , 5 (4): 403–434, doi: 10.1214/ss/1177012015 , JSTOR   2245366, MR   1092983 .
  5. ↑ Arratia, Richard (1983), "The motion of a tagged particle in the simple symmetric exclusion system on Z", Annals of Probability , 11 (2): 362–373, doi: 10.1214/aop/1176993602 , JSTOR   2243693, MR   0690134 .
  6. ↑ Arratia, R.; Gordon, L.; Waterman, M. S. (1990), "The Erdős-Rényi law in distribution, for coin tossing and sequence matching", Annals of Statistics , 18 (2): 539–570, doi: 10.1214/aos/1176347615 , MR   1056326 .
  7. ↑ Arratia, Richard; Waterman, Michael S. (1994), "A phase transition for the score in matching random sequences allowing deletions", Annals of Applied Probability , 4 (1): 200–225, doi: 10.1214/aoap/1177005208 , JSTOR   2245052, MR   1258181 .
Books
  1. ↑ Arratia, Richard; Barbour, A. D.; Tavaré, Simon (2003), Logarithmic Combinatorial Structures: A Probabilistic Approach, EMS Monographs in Mathematics, Zürich: European Mathematical Society, doi:10.4171/000, ISBN   3-03719-000-0, MR   2032426 .

Related Research Articles

Combinatorics is an area of mathematics primarily concerned with counting, both as a means and as an end to obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many applications ranging from logic to statistical physics and from evolutionary biology to computer science.

In combinatorial mathematics, the Bell numbers count the possible partitions of a set. These numbers have been studied by mathematicians since the 19th century, and their roots go back to medieval Japan. In an example of Stigler's law of eponymy, they are named after Eric Temple Bell, who wrote about them in the 1930s.

Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures.

<span class="mw-page-title-main">Béla Bollobás</span> Hungarian mathematician

Béla Bollobás FRS is a Hungarian-born British mathematician who has worked in various areas of mathematics, including functional analysis, combinatorics, graph theory, and percolation. He was strongly influenced by Paul Erdős from the age of 14.

In combinatorial mathematics, the Lubell–Yamamoto–Meshalkin inequality, more commonly known as the LYM inequality, is an inequality on the sizes of sets in a Sperner family, proved by Bollobás (1965), Lubell (1966), Meshalkin (1963), and Yamamoto (1954). It is named for the initials of three of its discoverers. To include the initials of all four discoverers, it is sometimes referred to as the YBLM inequality.

In mathematics, a combinatorial class is a countable set of mathematical objects, together with a size function mapping each object to a non-negative integer, such that there are finitely many objects of each size.

<span class="mw-page-title-main">Herbert Wilf</span> American mathematician

Herbert Saul Wilf was an American mathematician, specializing in combinatorics and graph theory. He was the Thomas A. Scott Professor of Mathematics in Combinatorial Analysis and Computing at the University of Pennsylvania. He wrote numerous books and research papers. Together with Neil Calkin he founded The Electronic Journal of Combinatorics in 1994 and was its editor-in-chief until 2001.

In the mathematical study of permutations and permutation patterns, a superpattern or universal permutation is a permutation that contains all of the patterns of a given length. More specifically, a k-superpattern contains all possible patterns of length k.

The Stanley–Wilf conjecture, formulated independently by Richard P. Stanley and Herbert Wilf in the late 1980s, states that the growth rate of every proper permutation class is singly exponential. It was proved by Adam Marcus and Gábor Tardos and is no longer a conjecture. Marcus and Tardos actually proved a different conjecture, due to Zoltán Füredi and Péter Hajnal, which had been shown to imply the Stanley–Wilf conjecture by Klazar (2000).

Stein's method is a general method in probability theory to obtain bounds on the distance between two probability distributions with respect to a probability metric. It was introduced by Charles Stein, who first published it in 1972, to obtain a bound between the distribution of a sum of -dependent sequence of random variables and a standard normal distribution in the Kolmogorov (uniform) metric and hence to prove not only a central limit theorem, but also bounds on the rates of convergence for the given metric.

In combinatorial mathematics and theoretical computer science, a (classical) permutation pattern is a sub-permutation of a longer permutation. Any permutation may be written in one-line notation as a sequence of entries representing the result of applying the permutation to the sequence 123...; for instance the sequence 213 represents the permutation on three elements that swaps elements 1 and 2. If π and σ are two permutations represented in this way, then π is said to contain σ as a pattern if some subsequence of the entries of π has the same relative order as all of the entries of σ.

In the study of permutation patterns, there has been considerable interest in enumerating specific permutation classes, especially those with relatively few basis elements. This area of study has turned up unexpected instances of Wilf equivalence, where two seemingly-unrelated permutation classes have the same numbers of permutations of each length.

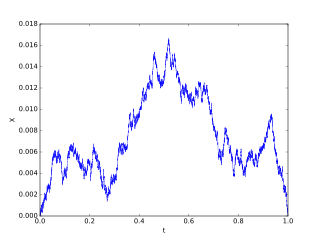
<span class="mw-page-title-main">Brownian excursion</span> Stochastic process

In probability theory a Brownian excursion process is a stochastic process that is closely related to a Wiener process. Realisations of Brownian excursion processes are essentially just realizations of a Wiener process selected to satisfy certain conditions. In particular, a Brownian excursion process is a Wiener process conditioned to be positive and to take the value 0 at time 1. Alternatively, it is a Brownian bridge process conditioned to be positive. BEPs are important because, among other reasons, they naturally arise as the limit process of a number of conditional functional central limit theorems.

<span class="mw-page-title-main">Lester Dubins</span> American mathematician

Lester Dubins was an American mathematician noted primarily for his research in probability theory. He was a faculty member at the University of California at Berkeley from 1962 through 2004, and in retirement was Professor Emeritus of Mathematics and Statistics.

Nicholas Charles Wormald is an Australian mathematician and professor of mathematics at Monash University. He specializes in probabilistic combinatorics, graph theory, graph algorithms, Steiner trees, web graphs, mine optimization, and other areas in combinatorics.

Rodica Eugenia Simion was a Romanian-American mathematician. She was the Columbian School Professor of Mathematics at George Washington University. Her research concerned combinatorics: she was a pioneer in the study of permutation patterns, and an expert on noncrossing partitions.

Russell David Lyons is an American mathematician, specializing in probability theory on graphs, combinatorics, statistical mechanics, ergodic theory and harmonic analysis.

<span class="mw-page-title-main">Erwin Bolthausen</span> Swiss mathematician (born 1945)

Erwin Bolthausen is a Swiss mathematician, specializing in probability theory, statistics, and stochastic models in mathematical physics.

Stephen Mitchell Samuels was a statistician and mathematician, known for his work on the secretary problem and for the Samuels Conjecture involving a Chebyshev-type inequality for sums of independent, non-negative random variables.

References

  1. ↑ Holst, Lars (2004), "Book Reviews: Logarithmic Combinatorial Structures: A Probabilistic Approach", Combinatorics, Probability and Computing , 13 (6): 916–917, doi:10.1017/S0963548304226566, S2CID   122978587 .
  2. ↑ Stark, Dudley (2005), "Book Reviews: Logarithmic Combinatorial Structures: A Probabilistic Approach", Bulletin of the London Mathematical Society, 37 (1): 157–158, doi:10.1112/S0024609304224092 .
  3. ↑ Richard Arratia at the Mathematics Genealogy Project
  4. ↑ Faculty listing, USC Mathematics, retrieved 2013-06-01.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.