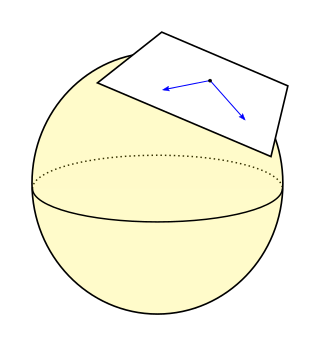
In differential geometry, a Riemannian manifold is a geometric space on which many geometric notions such as distance, angles, length, volume, and curvature are defined. Euclidean space, the -sphere, hyperbolic space, and smooth surfaces in three-dimensional space, such as ellipsoids and paraboloids, are all examples of Riemannian manifolds. Riemannian manifolds are named after German mathematician Bernhard Riemann, who first conceptualized them.

In the mathematical disciplines of topology and geometry, an orbifold is a generalization of a manifold. Roughly speaking, an orbifold is a topological space which is locally a finite group quotient of a Euclidean space.
In mathematics, real trees are a class of metric spaces generalising simplicial trees. They arise naturally in many mathematical contexts, in particular geometric group theory and probability theory. They are also the simplest examples of Gromov hyperbolic spaces.

Eliyahu Rips was an Israeli mathematician of Latvian origin known for his research in geometric group theory. He became known to the general public following his co-authoring a paper on what is popularly known as Bible code, the supposed coded messaging in the Hebrew text of the Torah.

Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups can act non-trivially.

In mathematics, a 3-manifold is a topological space that locally looks like a three-dimensional Euclidean space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane to a small and close enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below.
In mathematics, more precisely in topology and differential geometry, a hyperbolic 3-manifold is a manifold of dimension 3 equipped with a hyperbolic metric, that is a Riemannian metric which has all its sectional curvatures equal to −1. It is generally required that this metric be also complete: in this case the manifold can be realised as a quotient of the 3-dimensional hyperbolic space by a discrete group of isometries.

In mathematics, a hyperbolic manifold is a space where every point looks locally like hyperbolic space of some dimension. They are especially studied in dimensions 2 and 3, where they are called hyperbolic surfaces and hyperbolic 3-manifolds, respectively. In these dimensions, they are important because most manifolds can be made into a hyperbolic manifold by a homeomorphism. This is a consequence of the uniformization theorem for surfaces and the geometrization theorem for 3-manifolds proved by Perelman.
In mathematics, Mostow's rigidity theorem, or strong rigidity theorem, or Mostow–Prasad rigidity theorem, essentially states that the geometry of a complete, finite-volume hyperbolic manifold of dimension greater than two is determined by the fundamental group and hence unique. The theorem was proven for closed manifolds by Mostow and extended to finite volume manifolds by Marden (1974) in 3 dimensions, and by Prasad in all dimensions at least 3. Gromov (1981) gave an alternate proof using the Gromov norm. Besson, Courtois & Gallot (1996) gave the simplest available proof.

In group theory, more precisely in geometric group theory, a hyperbolic group, also known as a word hyperbolic group or Gromov hyperbolic group, is a finitely generated group equipped with a word metric satisfying certain properties abstracted from classical hyperbolic geometry. The notion of a hyperbolic group was introduced and developed by Mikhail Gromov. The inspiration came from various existing mathematical theories: hyperbolic geometry but also low-dimensional topology, and combinatorial group theory. In a very influential chapter from 1987, Gromov proposed a wide-ranging research program. Ideas and foundational material in the theory of hyperbolic groups also stem from the work of George Mostow, William Thurston, James W. Cannon, Eliyahu Rips, and many others.

In mathematics, a quasi-isometry is a function between two metric spaces that respects large-scale geometry of these spaces and ignores their small-scale details. Two metric spaces are quasi-isometric if there exists a quasi-isometry between them. The property of being quasi-isometric behaves like an equivalence relation on the class of metric spaces.
In mathematics, an ultralimit is a geometric construction that assigns a limit metric space to a sequence of metric spaces . The concept captures the limiting behavior of finite configurations in the spaces employing an ultrafilter to bypass the need for repeated consideration of subsequences to ensure convergence. Ultralimits generalize Gromov–Hausdorff convergence in metric spaces.
Bass–Serre theory is a part of the mathematical subject of group theory that deals with analyzing the algebraic structure of groups acting by automorphisms on simplicial trees. The theory relates group actions on trees with decomposing groups as iterated applications of the operations of free product with amalgamation and HNN extension, via the notion of the fundamental group of a graph of groups. Bass–Serre theory can be regarded as one-dimensional version of the orbifold theory.

Zlil Sela is an Israeli mathematician working in the area of geometric group theory. He is a Professor of Mathematics at the Hebrew University of Jerusalem. Sela is known for the solution of the isomorphism problem for torsion-free word-hyperbolic groups and for the solution of the Tarski conjecture about equivalence of first-order theories of finitely generated non-abelian free groups.
In mathematics, and more precisely in topology, the mapping class group of a surface, sometimes called the modular group or Teichmüller modular group, is the group of homeomorphisms of the surface viewed up to continuous deformation. It is of fundamental importance for the study of 3-manifolds via their embedded surfaces and is also studied in algebraic geometry in relation to moduli problems for curves.
In the mathematical subject of geometric group theory, the Švarc–Milnor lemma is a statement which says that a group , equipped with a "nice" discrete isometric action on a metric space , is quasi-isometric to .
In the mathematical subject of group theory, a co-Hopfian group is a group that is not isomorphic to any of its proper subgroups. The notion is dual to that of a Hopfian group, named after Heinz Hopf.
In the mathematical subject of geometric group theory, an acylindrically hyperbolic group is a group admitting a non-elementary 'acylindrical' isometric action on some geodesic hyperbolic metric space. This notion generalizes the notions of a hyperbolic group and of a relatively hyperbolic group and includes a significantly wider class of examples, such as mapping class groups and Out(Fn).
Godfrey Peter Scott, known as Peter Scott, was a British-American mathematician, known for the Scott core theorem.
In mathematics, a Cannon–Thurston map is any of a number of continuous group-equivariant maps between the boundaries of two hyperbolic metric spaces extending a discrete isometric actions of the group on those spaces.









