

In geometry, a Robbins pentagon is a cyclic pentagon whose side lengths and area are all rational numbers.


In geometry, a Robbins pentagon is a cyclic pentagon whose side lengths and area are all rational numbers.
Robbins pentagons were named by Buchholz & MacDougall (2008) after David P. Robbins, who had previously given a formula for the area of a cyclic pentagon as a function of its edge lengths. Buchholz and MacDougall chose this name by analogy with the naming of Heron triangles after Hero of Alexandria, the discoverer of Heron's formula for the area of a triangle as a function of its edge lengths.
Every Robbins pentagon may be scaled so that its sides and area are integers. More strongly, Buchholz and MacDougall showed that if the side lengths are all integers and the area is rational, then the area is necessarily also an integer, and the perimeter is necessarily an even number.
Buchholz and MacDougall also showed that, in every Robbins pentagon, either all five of the internal diagonals are rational numbers or none of them are. If the five diagonals are rational (the case called a Brahmagupta pentagon by Sastry (2005)), then the radius of its circumscribed circle must also be rational, and the pentagon may be partitioned into three Heronian triangles by cutting it along any two non-crossing diagonals, or into five Heronian triangles by cutting it along the five radii from the circle center to its vertices.
Buchholz and MacDougall performed computational searches for Robbins pentagons with irrational diagonals but were unable to find any. On the basis of this negative result they suggested that Robbins pentagons with irrational diagonals may not exist.

Area is the measure of a region's size on a surface. The area of a plane region or plane area refers to the area of a shape or planar lamina, while surface area refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve or the volume of a solid . Two different regions may have the same area ; by synecdoche, "area" sometimes is used to refer to the region, as in a "polygonal area".

In Euclidean plane geometry, a rectangle is a rectilinear convex polygon or a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal ; or a parallelogram containing a right angle. A rectangle with four sides of equal length is a square. The term "oblong" is used to refer to a non-square rectangle. A rectangle with vertices ABCD would be denoted as ABCD.

In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.
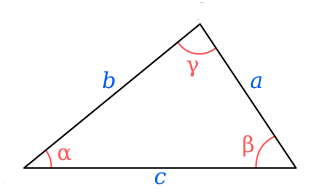
In geometry, Heron's formula gives the area of a triangle in terms of the three side lengths Letting be the semiperimeter of the triangle, the area is
In Euclidean geometry, Brahmagupta's formula, named after the 7th century Indian mathematician, is used to find the area of any cyclic quadrilateral given the lengths of the sides. Its generalized version, Bretschneider's formula, can be used with non-cyclic quadrilateral. Heron's formula can be thought as a special case of the Brahmagupta's formula for triangles.

In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and the circumradius respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case.
In geometry, an equilateral polygon is a polygon which has all sides of the same length. Except in the triangle case, an equilateral polygon does not need to also be equiangular, but if it does then it is a regular polygon. If the number of sides is at least four, an equilateral polygon does not need to be a convex polygon: it could be concave or even self-intersecting.

In geometry, an isosceles triangle is a triangle that has two sides of equal length. Sometimes it is specified as having exactly two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case. Examples of isosceles triangles include the isosceles right triangle, the golden triangle, and the faces of bipyramids and certain Catalan solids.
A Heronian tetrahedron is a tetrahedron whose edge lengths, face areas and volume are all integers. The faces must therefore all be Heronian triangles . Every Heronian tetrahedron can be arranged in Euclidean space so that its vertex coordinates are also integers.

In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.

In geometry, a set of points are said to be concyclic if they lie on a common circle. A polygon whose vertices are concyclic is called a cyclic polygon, and the circle is called its circumscribing circle or circumcircle. All concyclic points are equidistant from the center of the circle.

In Euclidean geometry, a square is a regular quadrilateral, which means that it has four straight sides of equal length and four equal angles. It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose internal angle, central angle, and external angle are all equal (90°), and whose diagonals are all equal in length. A square with vertices ABCD would be denoted ABCD.
In geometry, a Heronian triangle is a triangle whose side lengths a, b, and c and area A are all positive integers. Heronian triangles are named after Heron of Alexandria, based on their relation to Heron's formula which Heron demonstrated with the example triangle of sides 13, 14, 15 and area 84.
In mathematics, an Euler brick, named after Leonhard Euler, is a rectangular cuboid whose edges and face diagonals all have integer lengths. A primitive Euler brick is an Euler brick whose edge lengths are relatively prime. A perfect Euler brick is one whose space diagonal is also an integer, but such a brick has not yet been found.

A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist. For example, a right triangle may have angles that form simple relationships, such as 45°–45°–90°. This is called an "angle-based" right triangle. A "side-based" right triangle is one in which the lengths of the sides form ratios of whole numbers, such as 3 : 4 : 5, or of other special numbers such as the golden ratio. Knowing the relationships of the angles or ratios of sides of these special right triangles allows one to quickly calculate various lengths in geometric problems without resorting to more advanced methods.
Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. Geometry is one of the oldest mathematical sciences.
David Peter Robbins was an American mathematician. He is most famous for introducing alternating sign matrices. He is also known for his work on generalizations of Heron's formula on the area of polygons, due to which Robbins pentagons were named after him.
In geometry, a pentagon is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.

An integer triangle or integral triangle is a triangle all of whose side lengths are integers. A rational triangle is one whose side lengths are rational numbers; any rational triangle can be rescaled by the lowest common denominator of the sides to obtain a similar integer triangle, so there is a close relationship between integer triangles and rational triangles.
A Brahmagupta triangle is a triangle whose side lengths are consecutive positive integers and area is a positive integer. The triangle whose side lengths are 3, 4, 5 is a Brahmagupta triangle and so also is the triangle whose side lengths are 13, 14, 15. The Brahmagupta triangle is a special case of the Heronian triangle which is a triangle whose side lengths and area are all positive integers but the side lengths need not necessarily be consecutive integers. A Brahmagupta triangle is called as such in honor of the Indian astronomer and mathematician Brahmagupta who gave a list of the first eight such triangles without explaining the method by which he computed that list.