Rota's basis conjecture

Last updated

In linear algebra and matroid theory, Rota's basis conjecture is an unproven conjecture concerning rearrangements of bases, named after Gian-Carlo Rota. It states that, if X is either a vector space of dimension n or more generally a matroid of rank n, with n disjoint bases Bi, then it is possible to arrange the elements of these bases into an n × n matrix in such a way that the rows of the matrix are exactly the given bases and the columns of the matrix are also bases. That is, it should be possible to find a second set of n disjoint bases Ci, each of which consists of one element from each of the bases Bi.

Contents

Examples

The nine vertices of three colored triangles (red, blue, and yellow) regrouped into three rainbow triangles (black edges) Rota's basis conjecture 2.svg
The nine vertices of three colored triangles (red, blue, and yellow) regrouped into three rainbow triangles (black edges)

Rota's basis conjecture has a simple formulation for points in the Euclidean plane: it states that, given three triangles with distinct vertices, with each triangle colored with one of three colors, it must be possible to regroup the nine triangle vertices into three "rainbow" triangles having one vertex of each color. The triangles are all required to be non-degenerate, meaning that they do not have all three vertices on a line.

To see this as an instance of the basis conjecture, one may use either linear independence of the vectors () in a three-dimensional real vector space (where () are the Cartesian coordinates of the triangle vertices) or equivalently one may use a matroid of rank three in which a set S of points is independent if either |S| ≤ 2 or S forms the three vertices of a non-degenerate triangle. For this linear algebra and this matroid, the bases are exactly the non-degenerate triangles. Given the three input triangles and the three rainbow triangles, it is possible to arrange the nine vertices into a 3 × 3 matrix in which each row contains the vertices of one of the single-color triangles and each column contains the vertices of one of the rainbow triangles.

Analogously, for points in three-dimensional Euclidean space, the conjecture states that the sixteen vertices of four non-degenerate tetrahedra of four different colors may be regrouped into four rainbow tetrahedra.

Partial results

The statement of Rota's basis conjecture was first published by Huang & Rota (1994), crediting it (without citation) to Rota in 1989. [1] The basis conjecture has been proven for paving matroids (for all n) [2] and for the case n ≤ 3 (for all types of matroid). [3] For arbitrary matroids, it is possible to arrange the basis elements into a matrix the first Ω(√n) columns of which are bases. [4] The basis conjecture for linear algebras over fields of characteristic zero and for even values of n would follow from another conjecture on Latin squares by Alon and Tarsi. [1] [5] Based on this implication, the conjecture is known to be true for linear algebras over the real numbers for infinitely many values of n. [6]

In connection with Tverberg's theorem, Bárány & Larman (1992) conjectured that, for every set of r (d + 1) points in d-dimensional Euclidean space, colored with d + 1 colors in such a way that there are r points of each color, there is a way to partition the points into rainbow simplices (sets of d + 1 points with one point of each color) in such a way that the convex hulls of these sets have a nonempty intersection. [7] For instance, the two-dimensional case (proven by Bárány and Larman) with r = 3 states that, for every set of nine points in the plane, colored with three colors and three points of each color, it is possible to partition the points into three intersecting rainbow triangles, a statement similar to Rota's basis conjecture which states that it is possible to partition the points into three non-degenerate rainbow triangles. The conjecture of Bárány and Larman allows a collinear triple of points to be considered as a rainbow triangle, whereas Rota's basis conjecture disallows this; on the other hand, Rota's basis conjecture does not require the triangles to have a common intersection. Substantial progress on the conjecture of Bárány and Larman was made by Blagojević, Matschke & Ziegler (2009). [8]

See also

Related Research Articles

In combinatorics, a branch of mathematics, a matroid is a structure that abstracts and generalizes the notion of linear independence in vector spaces. There are many equivalent ways to define a matroid axiomatically, the most significant being in terms of: independent sets; bases or circuits; rank functions; closure operators; and closed sets or flats. In the language of partially ordered sets, a finite matroid is equivalent to a geometric lattice.

Discrete geometry Branch of geometry that studies combinatorial properties and constructive methods

Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object.

In the mathematical theory of matroids, a graphic matroid is a matroid whose independent sets are the forests in a given finite undirected graph. The dual matroids of graphic matroids are called co-graphic matroids or bond matroids. A matroid that is both graphic and co-graphic is sometimes called a planar matroid ; these are exactly the graphic matroids formed from planar graphs.

Carathéodorys theorem (convex hull) Point in the convex hull of a set P in Rd, is the convex combination of d+1 points in P

Carathéodory's theorem is a theorem in convex geometry. It states that if a point x of Rd lies in the convex hull of a set P, then x can be written as the convex combination of at most d + 1 points in P. Namely, there is a subset P′ of P consisting of d + 1 or fewer points such that x lies in the convex hull of P′. Equivalently, x lies in an r-simplex with vertices in P, where . The smallest r that makes the last statement valid for each x in the convex hull of P is defined as the Carathéodory's number of P. Depending on the properties of P, upper bounds lower than the one provided by Carathéodory's theorem can be obtained. Note that P need not be itself convex. A consequence of this is that P′ can always be extremal in P, as non-extremal points can be removed from P without changing the membership of x in the convex hull.

Sylvester–Gallai theorem Existence of a line through two points

The Sylvester–Gallai theorem in geometry states that every finite set of points in the Euclidean plane has a line that passes through exactly two of the points or a line that passes through all of them. It is named after James Joseph Sylvester, who posed it as a problem in 1893, and Tibor Gallai, who published one of the first proofs of this theorem in 1944.

The Fulkerson Prize for outstanding papers in the area of discrete mathematics is sponsored jointly by the Mathematical Optimization Society (MOS) and the American Mathematical Society (AMS). Up to three awards of $1,500 each are presented at each (triennial) International Symposium of the MOS. Originally, the prizes were paid out of a memorial fund administered by the AMS that was established by friends of the late Delbert Ray Fulkerson to encourage mathematical excellence in the fields of research exemplified by his work. The prizes are now funded by an endowment administered by MPS.

Convex polytope Convex hull of a finite set of points in a Euclidean space

A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the -dimensional Euclidean space . Most texts use the term "polytope" for a bounded convex polytope, and the word "polyhedron" for the more general, possibly unbounded object. Others allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts identify a convex polytope with its boundary.

In mathematics, a colored matroid is a matroid whose elements are labeled from a set of colors, which can be any set that suits the purpose, for instance the set of the first n positive integers, or the sign set {+, −}.

In mathematics, the Burr–Erdős conjecture was a problem concerning the Ramsey number of sparse graphs. The conjecture is named after Stefan Burr and Paul Erdős, and is one of many conjectures named after Erdős; it states that the Ramsey number of graphs in any sparse family of graphs should grow linearly in the number of vertices of the graph.

Tverbergs theorem On partitioning finite point sets into subsets with intersecting convex hulls

In discrete geometry, Tverberg's theorem, first stated by Helge Tverberg (1966), is the result that sufficiently many points in d-dimensional Euclidean space can be partitioned into subsets with intersecting convex hulls. Specifically, for any set of

Algebraic combinatorics Area of combinatorics

Algebraic combinatorics is an area of mathematics that employs methods of abstract algebra, notably group theory and representation theory, in various combinatorial contexts and, conversely, applies combinatorial techniques to problems in algebra.

In geometry, the moment curve is an algebraic curve in d-dimensional Euclidean space given by the set of points with Cartesian coordinates of the form

Criss-cross algorithm Method for mathematical optimization

In mathematical optimization, the criss-cross algorithm is any of a family of algorithms for linear programming. Variants of the criss-cross algorithm also solve more general problems with linear inequality constraints and nonlinear objective functions; there are criss-cross algorithms for linear-fractional programming problems, quadratic-programming problems, and linear complementarity problems.

In the mathematics of structural rigidity, a rigidity matroid is a matroid that describes the number of degrees of freedom of an undirected graph with rigid edges of fixed lengths, embedded into Euclidean space. In a rigidity matroid for a graph with n vertices in d-dimensional space, a set of edges that defines a subgraph with k degrees of freedom has matroid rank dn − k. A set of edges is independent if and only if, for every edge in the set, removing the edge would increase the number of degrees of freedom of the remaining subgraph.

Rota's excluded minors conjecture is one of a number of conjectures made by mathematician Gian-Carlo Rota. It is considered to be an important problem by some members of the structural combinatorics community. Rota conjectured in 1971 that, for every finite field, the family of matroids that can be represented over that field has only finitely many excluded minors. A proof of the conjecture has been announced by Geelen, Gerards, and Whittle.

In the mathematical theory of matroids, a matroid representation is a family of vectors whose linear independence relation is the same as that of a given matroid. Matroid representations are analogous to group representations; both types of representation provide abstract algebraic structures with concrete descriptions in terms of linear algebra.

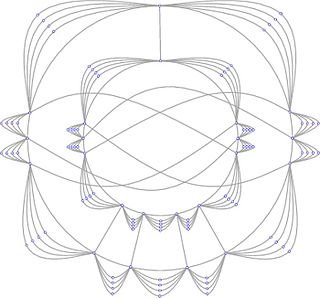
Topological graph

In mathematics, a topological graph is a representation of a graph in the plane, where the vertices of the graph are represented by distinct points and the edges by Jordan arcs joining the corresponding pairs of points. The points representing the vertices of a graph and the arcs representing its edges are called the vertices and the edges of the topological graph. It is usually assumed that any two edges of a topological graph cross a finite number of times, no edge passes through a vertex different from its endpoints, and no two edges touch each other. A topological graph is also called a drawing of a graph.

In graph theory, a branch of mathematics, an indifference graph is an undirected graph constructed by assigning a real number to each vertex and connecting two vertices by an edge when their numbers are within one unit of each other. Indifference graphs are also the intersection graphs of sets of unit intervals, or of properly nested intervals. Based on these two types of interval representations, these graphs are also called unit interval graphs or proper interval graphs; they form a subclass of the interval graphs.

Matroid parity problem Largest independent set of paired elements

In combinatorial optimization, the matroid parity problem is a problem of finding the largest independent set of paired elements in a matroid. The problem was formulated by Lawler (1976) as a common generalization of graph matching and matroid intersection. It is also known as polymatroid matching, or the matchoid problem.

In polyhedral combinatorics, the Gale transform turns the vertices of any convex polytopes into a set of vectors or points in a space of a different dimension, the Gale diagram of the polytope. It can be used to describe high-dimensional polytopes with few vertices, by transforming them into sets of points in a space of a much lower dimension. The process can also be reversed, to construct polytopes with desired properties from their Gale diagrams. The Gale transform and Gale diagram are named after David Gale, who introduced these methods in a 1956 paper on neighborly polytopes.

References

  1. 1 2 Huang, Rosa; Rota, Gian-Carlo (1994), "On the relations of various conjectures on Latin squares and straightening coefficients", Discrete Mathematics , 128 (1–3): 225–236, doi: 10.1016/0012-365X(94)90114-7 , MR   1271866 . See in particular Conjecture 4, p. 226.
  2. ↑ Geelen, Jim; Humphries, Peter J. (2006), "Rota's basis conjecture for paving matroids" (PDF), SIAM Journal on Discrete Mathematics , 20 (4): 1042–1045, CiteSeerX   10.1.1.63.6806 , doi:10.1137/060655596, MR   2272246 .
  3. ↑ Chan, Wendy (1995), "An exchange property of matroid", Discrete Mathematics , 146 (1–3): 299–302, doi: 10.1016/0012-365X(94)00071-3 , MR   1360125 .
  4. ↑ Geelen, Jim; Webb, Kerri (2007), "On Rota's basis conjecture" (PDF), SIAM Journal on Discrete Mathematics , 21 (3): 802–804, doi:10.1137/060666494, MR   2354007 .
  5. ↑ Onn, Shmuel (1997), "A colorful determinantal identity, a conjecture of Rota, and Latin squares", The American Mathematical Monthly , 104 (2): 156–159, doi:10.2307/2974985, JSTOR   2974985, MR   1437419 .
  6. ↑ Glynn, David G. (2010), "The conjectures of Alon–Tarsi and Rota in dimension prime minus one", SIAM Journal on Discrete Mathematics , 24 (2): 394–399, doi:10.1137/090773751, MR   2646093 .
  7. ↑ Bárány, I.; Larman, D. G. (1992), "A colored version of Tverberg's theorem", Journal of the London Mathematical Society, Second Series, 45 (2): 314–320, CiteSeerX   10.1.1.108.9781 , doi:10.1112/jlms/s2-45.2.314, MR   1171558 .
  8. ↑ Blagojević, Pavle V. M.; Matschke, Benjamin; Ziegler, Günter M. (2009), Optimal bounds for the colored Tverberg problem, arXiv: 0910.4987 , Bibcode:2009arXiv0910.4987B .
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.