Rprop

Last updated

Rprop, short for resilient backpropagation, is a learning heuristic for supervised learning in feedforward artificial neural networks. This is a first-order optimization algorithm. This algorithm was created by Martin Riedmiller and Heinrich Braun in 1992. [1]

Contents

Similarly to the Manhattan update rule, Rprop takes into account only the sign of the partial derivative over all patterns (not the magnitude), and acts independently on each "weight". For each weight, if there was a sign change of the partial derivative of the total error function compared to the last iteration, the update value for that weight is multiplied by a factor η−, where η− < 1. If the last iteration produced the same sign, the update value is multiplied by a factor of η+, where η+ > 1. The update values are calculated for each weight in the above manner, and finally each weight is changed by its own update value, in the opposite direction of that weight's partial derivative, so as to minimise the total error function. η+ is empirically set to 1.2 and η− to 0.5.[ citation needed ]

Rprop can result in very large weight increments or decrements if the gradients are large, which is a problem when using mini-batches as opposed to full batches. RMSprop addresses this problem by keeping the moving average of the squared gradients for each weight and dividing the gradient by the square root of the mean square. [2]

RPROP is a batch update algorithm. Next to the cascade correlation algorithm and the Levenberg–Marquardt algorithm, Rprop is one of the fastest weight update mechanisms.[ citation needed ]

Variations

Martin Riedmiller developed three algorithms, all named RPROP. Igel and Hüsken assigned names to them and added a new variant: [3] [4]

  1. RPROP+ is defined at A Direct Adaptive Method for Faster Backpropagation Learning: The RPROP Algorithm. [5]
  2. RPROP− is defined at Advanced Supervised Learning in Multi-layer Perceptrons – From Backpropagation to Adaptive Learning Algorithms. Backtracking is removed from RPROP+. [6]
  3. iRPROP− is defined in Rprop – Description and Implementation Details [7] and was reinvented by Igel and Hüsken. [4] This variant is very popular and most simple.
  4. iRPROP+ is defined at Improving the Rprop Learning Algorithm and is very robust and typically faster than the other three variants. [3] [4]

Related Research Articles

<span class="mw-page-title-main">Artificial neural network</span> Computational model used in machine learning, based on connected, hierarchical functions

Artificial neural networks (ANNs), usually simply called neural networks (NNs) or neural nets, are computing systems inspired by the biological neural networks that constitute animal brains.

<span class="mw-page-title-main">Perceptron</span> Algorithm for supervised learning of binary classifiers

In machine learning, the perceptron is an algorithm for supervised learning of binary classifiers. A binary classifier is a function which can decide whether or not an input, represented by a vector of numbers, belongs to some specific class. It is a type of linear classifier, i.e. a classification algorithm that makes its predictions based on a linear predictor function combining a set of weights with the feature vector.

An artificial neuron is a mathematical function conceived as a model of biological neurons, a neural network. Artificial neurons are elementary units in an artificial neural network. The artificial neuron receives one or more inputs and sums them to produce an output. Usually each input is separately weighted, and the sum is passed through a non-linear function known as an activation function or transfer function. The transfer functions usually have a sigmoid shape, but they may also take the form of other non-linear functions, piecewise linear functions, or step functions. They are also often monotonically increasing, continuous, differentiable and bounded. Non-monotonic, unbounded and oscillating activation functions with multiple zeros that outperform sigmoidal and ReLU like activation functions on many tasks have also been recently explored. The thresholding function has inspired building logic gates referred to as threshold logic; applicable to building logic circuits resembling brain processing. For example, new devices such as memristors have been extensively used to develop such logic in recent times.

<span class="mw-page-title-main">Stochastic gradient descent</span> Optimization algorithm

Stochastic gradient descent is an iterative method for optimizing an objective function with suitable smoothness properties. It can be regarded as a stochastic approximation of gradient descent optimization, since it replaces the actual gradient by an estimate thereof. Especially in high-dimensional optimization problems this reduces the very high computational burden, achieving faster iterations in exchange for a lower convergence rate.

In machine learning, the delta rule is a gradient descent learning rule for updating the weights of the inputs to artificial neurons in a single-layer neural network. It is a special case of the more general backpropagation algorithm. For a neuron with activation function , the delta rule for neuron 's th weight is given by

<span class="mw-page-title-main">Backpropagation</span> Optimization algorithm for artificial neural networks

In machine learning, backpropagation is a widely used algorithm for training feedforward artificial neural networks or other parameterized networks with differentiable nodes. It is an efficient application of the Leibniz chain rule (1673) to such networks. It is also known as the reverse mode of automatic differentiation or reverse accumulation, due to Seppo Linnainmaa (1970). The term "back-propagating errors" was introduced in 1962 by Frank Rosenblatt, but he did not know how to implement this, although Henry J. Kelley had a continuous precursor of backpropagation already in 1960 in the context of control theory.

<span class="mw-page-title-main">Recurrent neural network</span> Computational model used in machine learning

A recurrent neural network (RNN) is a class of artificial neural networks where connections between nodes can create a cycle, allowing output from some nodes to affect subsequent input to the same nodes. This allows it to exhibit temporal dynamic behavior. Derived from feedforward neural networks, RNNs can use their internal state (memory) to process variable length sequences of inputs. This makes them applicable to tasks such as unsegmented, connected handwriting recognition or speech recognition. Recurrent neural networks are theoretically Turing complete and can run arbitrary programs to process arbitrary sequences of inputs.

<span class="mw-page-title-main">Feedforward neural network</span> Type of artificial neural network

A feedforward neural network (FNN) is an artificial neural network wherein connections between the nodes do not form a cycle. As such, it is different from its descendant: recurrent neural networks.

<span class="mw-page-title-main">Multilayer perceptron</span> Type of feedforward neural network

A multilayer perceptron (MLP) is a fully connected class of feedforward artificial neural network (ANN). The term MLP is used ambiguously, sometimes loosely to mean any feedforward ANN, sometimes strictly to refer to networks composed of multiple layers of perceptrons ; see § Terminology. Multilayer perceptrons are sometimes colloquially referred to as "vanilla" neural networks, especially when they have a single hidden layer.

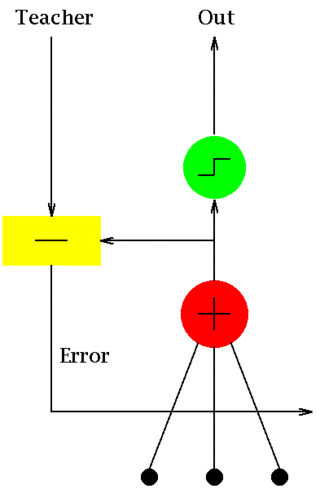
<span class="mw-page-title-main">ADALINE</span> Early single-layer artificial neural network

ADALINE is an early single-layer artificial neural network and the name of the physical device that implemented this network. The network uses memistors. It was developed by Professor Bernard Widrow and his doctoral student Ted Hoff at Stanford University in 1960. It is based on the McCulloch–Pitts neuron. It consists of a weight, a bias and a summation function.

<span class="mw-page-title-main">Online machine learning</span> Method of machine learning

In computer science, online machine learning is a method of machine learning in which data becomes available in a sequential order and is used to update the best predictor for future data at each step, as opposed to batch learning techniques which generate the best predictor by learning on the entire training data set at once. Online learning is a common technique used in areas of machine learning where it is computationally infeasible to train over the entire dataset, requiring the need of out-of-core algorithms. It is also used in situations where it is necessary for the algorithm to dynamically adapt to new patterns in the data, or when the data itself is generated as a function of time, e.g., stock price prediction. Online learning algorithms may be prone to catastrophic interference, a problem that can be addressed by incremental learning approaches.

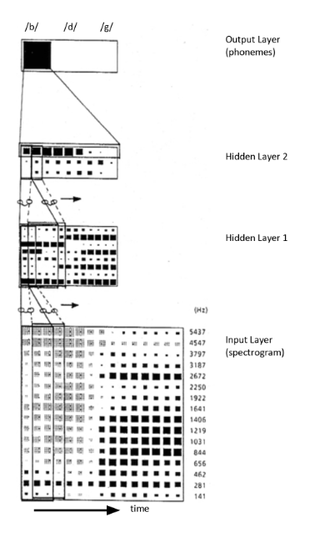
<span class="mw-page-title-main">Time delay neural network</span>

Time delay neural network (TDNN) is a multilayer artificial neural network architecture whose purpose is to 1) classify patterns with shift-invariance, and 2) model context at each layer of the network.

<span class="mw-page-title-main">Encog</span> Machine learning framework

Encog is a machine learning framework available for Java and .Net. Encog supports different learning algorithms such as Bayesian Networks, Hidden Markov Models and Support Vector Machines. However, its main strength lies in its neural network algorithms. Encog contains classes to create a wide variety of networks, as well as support classes to normalize and process data for these neural networks. Encog trains using many different techniques. Multithreading is used to allow optimal training performance on multicore machines.

There are many types of artificial neural networks (ANN).

<span class="mw-page-title-main">Restricted Boltzmann machine</span> Class of artificial neural network

A restricted Boltzmann machine (RBM) is a generative stochastic artificial neural network that can learn a probability distribution over its set of inputs.

An artificial neural network's learning rule or learning process is a method, mathematical logic or algorithm which improves the network's performance and/or training time. Usually, this rule is applied repeatedly over the network. It is done by updating the weights and bias levels of a network when a network is simulated in a specific data environment. A learning rule may accept existing conditions of the network and will compare the expected result and actual result of the network to give new and improved values for weights and bias. Depending on the complexity of actual model being simulated, the learning rule of the network can be as simple as an XOR gate or mean squared error, or as complex as the result of a system of differential equations.

<span class="mw-page-title-main">Vanishing gradient problem</span> Machine learning model training problem

In machine learning, the vanishing gradient problem is encountered when training artificial neural networks with gradient-based learning methods and backpropagation. In such methods, during each iteration of training each of the neural network's weights receives an update proportional to the partial derivative of the error function with respect to the current weight. The problem is that in some cases, the gradient will be vanishingly small, effectively preventing the weight from changing its value. In the worst case, this may completely stop the neural network from further training. As one example of the problem cause, traditional activation functions such as the hyperbolic tangent function have gradients in the range (0,1], and backpropagation computes gradients by the chain rule. This has the effect of multiplying n of these small numbers to compute gradients of the early layers in an n-layer network, meaning that the gradient decreases exponentially with n while the early layers train very slowly.

<span class="mw-page-title-main">Residual neural network</span> Type of artificial neural network

A residual neural network (ResNet) is an artificial neural network (ANN). It is a gateless or open-gated variant of the HighwayNet, the first working very deep feedforward neural network with hundreds of layers, much deeper than previous neural networks. Skip connections or shortcuts are used to jump over some layers . Typical ResNet models are implemented with double- or triple- layer skips that contain nonlinearities (ReLU) and batch normalization in between. Models with several parallel skips are referred to as DenseNets. In the context of residual neural networks, a non-residual network may be described as a plain network.

<span class="mw-page-title-main">Learning rate</span> Tuning parameter (hyperparameter) in optimization

In machine learning and statistics, the learning rate is a tuning parameter in an optimization algorithm that determines the step size at each iteration while moving toward a minimum of a loss function. Since it influences to what extent newly acquired information overrides old information, it metaphorically represents the speed at which a machine learning model "learns". In the adaptive control literature, the learning rate is commonly referred to as gain.

References

  1. ↑ Martin Riedmiller und Heinrich Braun: Rprop - A Fast Adaptive Learning Algorithm. Proceedings of the International Symposium on Computer and Information Science VII, 1992
  2. ↑ https://towardsdatascience.com/understanding-rmsprop-faster-neural-network-learning-62e116fcf29a
  3. 1 2 Christian Igel and Michael Hüsken. Improving the Rprop Learning Algorithm. Second International Symposium on Neural Computation (NC 2000), pp. 115-121, ICSC Academic Press, 2000
  4. 1 2 3 Christian Igel and Michael Hüsken. Empirical Evaluation of the Improved Rprop Learning Algorithm. Neurocomputing 50:105-123, 2003
  5. ↑ Martin Riedmiller and Heinrich Braun. A direct adaptive method for faster backpropagation learning: The Rprop algorithm. Proceedings of the IEEE International Conference on Neural Networks, 586-591, IEEE Press, 1993
  6. ↑ Martin Riedmiller. Advanced supervised learning in multi-layer perceptrons - From backpropagation to adaptive learning algorithms. Computer Standards and Interfaces 16(5), 265-278, 1994
  7. ↑ Martin Riedmiller. Rprop – Description and Implementation Details. Technical report, 1994
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.