SNePS is a knowledge representation, reasoning, and acting (KRRA) system developed and maintained by Stuart C. Shapiro and colleagues at the State University of New York at Buffalo.
SNePS is simultaneously a logic-based, frame-based, and network-based KRRA system. It uses an assertional model of knowledge, in that a SNePS knowledge base (KB) consists of a set of assertions (propositions) about various entities. Its intended model is of an intensional domain of mental entities—the entities conceived of by some agent, and the propositions believed by it. The intensionality is primarily accomplished by the absence of a built-in equality operator, since any two syntactically different terms might have slightly different Fregean senses.
SNePS has three styles of inference: formula-based, derived from its logic-based personality; slot-based, derived from its frame-based personality; and path-based, derived from its network-based personality. However, all three are integrated, operating together.
SNePS may be used as a stand-alone KRR system. It has also been used, along with its integrated acting component, to implement the mind of intelligent agents (cognitive robots), in accord with the GLAIR agent architecture (a layered cognitive architecture). The SNePS Research Group often calls its agents Cassie.
As a logic-based system, a SNePS KB consists of a set of terms, and functions and formulas over those terms. The set of logical connectives and quantifiers extends the usual set used by first-order logics, all taking one or more arbitrarily-sized sets of arguments. In accord with the intended use of SNePS to represent the mind of a natural-language-competent intelligent agent, propositions are first-class entities of the intended domain, so formulas are actually proposition-denoting functional terms. SNePSLOG, the input-output language of the logic-based face of SNePS, looks like a naive logic in that function symbols (including "predicates"), and formulas (actually proposition-denoting terms) may be the arguments of functions and may be quantified over. The underlying SNePS, however, is a first order logic, with the user's function symbols and formulas reified.
Formula-based inference is implemented as a natural-deduction-style inference engine in which there are introduction and elimination rules for the connectives and quantifiers. SNePS formula-based inference is sound but not complete, as rules of inference that are less useful for natural language understanding and commonsense reasoning have not been implemented.
A proposition-denoting term in a SNePS KB might or might not be "asserted", that is, treated as true in the KB. The SNePS logic is a paraconsistent version of relevance logic, so that a contradiction does not imply anything whatsoever. Nevertheless, SNeBR, the SNePS Belief Revision subsystem, will notice any explicit contradiction and engage the user in a dialogue to repair it. SNeBR is an Assumption-Based Truth Maintenance System (ATMS), and removes the assertion status of any proposition whose support has been removed.
As a frame-based system, every SNePS functional term (including proposition-valued terms) is represented by a frame with slots and fillers. Each slot may be filled by an arbitrarily-sized set of other terms. However, cycles cannot be constructed. SNePSUL, the SNePS User Language is an input-output language for interacting with SNePS in its guise as a frame-based system.
SNePSLOG may be used in any of three modes. In two modes, the caseframe (set of slots) associated with each functional term is determined by the system. In mode 3, the user declares what caseframe is to be used for each function symbol.
In slot-based inference, any proposition-valued frame is considered to imply the frame with any of its slots filled by a subset of its fillers. In the current implementation, this is not always sound.
As a network-based system, SNePS is a propositional semantic network, thus the original meaning of "SNePS" as "The Semantic Network Processing System". This view is obtained by considering every individual constant and every functional term to be a node of the network, and every slot to be a directed labeled arc from the frame-node it is in to every node in its filler. In the intended interpretation, every node denotes a mental entity, some of which are propositions, and every proposition represented in the network is represented by the node that denotes it. Some nodes are variables of the SNePS logic, and they range over nodes, and only over nodes.
Path-based inference rules may be defined, although they, themselves, are not represented in SNePS. A path-based inference rule specifies that some labeled arc r may be inferred as present from some node n to some other node m just in case a given path exists from n to m. There is an extensive recursive set of path constructors available.
SNePS has been used for a variety of KRR tasks, for natural language understanding and generation, for commonsense reasoning, and for cognitive robotics. It has been used in several KR courses around the world.
SNePS is implemented as a platform-independent system in Common Lisp and is freely available.
An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Ancient Greek word ἀξίωμα (axíōma), meaning 'that which is thought worthy or fit' or 'that which commends itself as evident'.

Cyc is a long-term artificial intelligence project that aims to assemble a comprehensive ontology and knowledge base that spans the basic concepts and rules about how the world works. Hoping to capture common sense knowledge, Cyc focuses on implicit knowledge that other AI platforms may take for granted. This is contrasted with facts one might find somewhere on the internet or retrieve via a search engine or Wikipedia. Cyc enables semantic reasoners to perform human-like reasoning and be less "brittle" when confronted with novel situations.
First-order logic—also known as predicate logic, quantificational logic, and first-order predicate calculus—is a collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantified variables over non-logical objects, and allows the use of sentences that contain variables, so that rather than propositions such as "Socrates is a man", one can have expressions in the form "there exists x such that x is Socrates and x is a man", where "there exists" is a quantifier, while x is a variable. This distinguishes it from propositional logic, which does not use quantifiers or relations; in this sense, propositional logic is the foundation of first-order logic.
Knowledge representation and reasoning is the field of artificial intelligence (AI) dedicated to representing information about the world in a form that a computer system can use to solve complex tasks such as diagnosing a medical condition or having a dialog in a natural language. Knowledge representation incorporates findings from psychology about how humans solve problems and represent knowledge in order to design formalisms that will make complex systems easier to design and build. Knowledge representation and reasoning also incorporates findings from logic to automate various kinds of reasoning, such as the application of rules or the relations of sets and subsets.
In logic, the law of excluded middle states that for every proposition, either this proposition or its negation is true. It is one of the so-called three laws of thought, along with the law of noncontradiction, and the law of identity. However, no system of logic is built on just these laws, and none of these laws provides inference rules, such as modus ponens or De Morgan's laws.
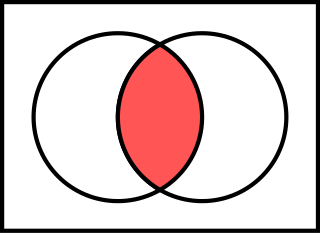
In logic, mathematics and linguistics, And is the truth-functional operator of logical conjunction; the and of a set of operands is true if and only if all of its operands are true. The logical connective that represents this operator is typically written as or ⋅ .
Propositional calculus is a branch of logic. It is also called propositional logic, statement logic, sentential calculus, sentential logic, or sometimes zeroth-order logic. It deals with propositions and relations between propositions, including the construction of arguments based on them. Compound propositions are formed by connecting propositions by logical connectives. Propositions that contain no logical connectives are called atomic propositions.

In mathematics, a theorem is a statement that has been proved, or can be proved. The proof of a theorem is a logical argument that uses the inference rules of a deductive system to establish that the theorem is a logical consequence of the axioms and previously proved theorems.
In mathematical logic, a sequent is a very general kind of conditional assertion.
Understood in a narrow sense, philosophical logic is the area of logic that studies the application of logical methods to philosophical problems, often in the form of extended logical systems like modal logic. Some theorists conceive philosophical logic in a wider sense as the study of the scope and nature of logic in general. In this sense, philosophical logic can be seen as identical to the philosophy of logic, which includes additional topics like how to define logic or a discussion of the fundamental concepts of logic. The current article treats philosophical logic in the narrow sense, in which it forms one field of inquiry within the philosophy of logic.
Reason maintenance is a knowledge representation approach to efficient handling of inferred information that is explicitly stored. Reason maintenance distinguishes between base facts, which can be defeated, and derived facts. As such it differs from belief revision which, in its basic form, assumes that all facts are equally important. Reason maintenance was originally developed as a technique for implementing problem solvers. It encompasses a variety of techniques that share a common architecture: two components—a reasoner and a reason maintenance system—communicate with each other via an interface. The reasoner uses the reason maintenance system to record its inferences and justifications of the inferences. The reasoner also informs the reason maintenance system which are the currently valid base facts (assumptions). The reason maintenance system uses the information to compute the truth value of the stored derived facts and to restore consistency if an inconsistency is derived.
Kripke semantics is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke and André Joyal. It was first conceived for modal logics, and later adapted to intuitionistic logic and other non-classical systems. The development of Kripke semantics was a breakthrough in the theory of non-classical logics, because the model theory of such logics was almost non-existent before Kripke.
The laws of thought are fundamental axiomatic rules upon which rational discourse itself is often considered to be based. The formulation and clarification of such rules have a long tradition in the history of philosophy and logic. Generally they are taken as laws that guide and underlie everyone's thinking, thoughts, expressions, discussions, etc. However, such classical ideas are often questioned or rejected in more recent developments, such as intuitionistic logic, dialetheism and fuzzy logic.
In propositional logic, a propositional formula is a type of syntactic formula which is well formed and has a truth value. If the values of all variables in a propositional formula are given, it determines a unique truth value. A propositional formula may also be called a propositional expression, a sentence, or a sentential formula.
In mathematical logic, a tautology is a formula or assertion that is true in every possible interpretation. An example is "x=y or x≠y". Similarly, "either the ball is green, or the ball is not green" is always true, regardless of the colour of the ball.
Logic is the formal science of using reason and is considered a branch of both philosophy and mathematics and to a lesser extent computer science. Logic investigates and classifies the structure of statements and arguments, both through the study of formal systems of inference and the study of arguments in natural language. The scope of logic can therefore be very large, ranging from core topics such as the study of fallacies and paradoxes, to specialized analyses of reasoning such as probability, correct reasoning, and arguments involving causality. One of the aims of logic is to identify the correct and incorrect inferences. Logicians study the criteria for the evaluation of arguments.
Philosophy of logic is the area of philosophy that studies the scope and nature of logic. It investigates the philosophical problems raised by logic, such as the presuppositions often implicitly at work in theories of logic and in their application. This involves questions about how logic is to be defined and how different logical systems are connected to each other. It includes the study of the nature of the fundamental concepts used by logic and the relation of logic to other disciplines. According to a common characterization, philosophical logic is the part of the philosophy of logic that studies the application of logical methods to philosophical problems, often in the form of extended logical systems like modal logic. But other theorists draw the distinction between the philosophy of logic and philosophical logic differently or not at all. Metalogic is closely related to the philosophy of logic as the discipline investigating the properties of formal logical systems, like consistency and completeness.
This glossary of artificial intelligence is a list of definitions of terms and concepts relevant to the study of artificial intelligence, its sub-disciplines, and related fields. Related glossaries include Glossary of computer science, Glossary of robotics, and Glossary of machine vision.
The Mivar-based approach is a mathematical tool for designing artificial intelligence (AI) systems. Mivar was developed by combining production and Petri nets. The Mivar-based approach was developed for semantic analysis and adequate representation of humanitarian epistemological and axiological principles in the process of developing artificial intelligence. The Mivar-based approach incorporates computer science, informatics and discrete mathematics, databases, expert systems, graph theory, matrices and inference systems. The Mivar-based approach involves two technologies: