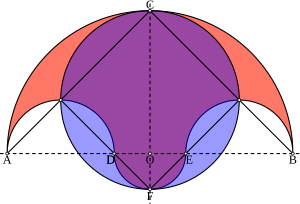
The salinon (meaning 'salt-cellar' in Greek) is a geometrical figure that consists of four semicircles. It was first introduced in the Book of Lemmas , a work attributed to Archimedes. [1]

The salinon (meaning 'salt-cellar' in Greek) is a geometrical figure that consists of four semicircles. It was first introduced in the Book of Lemmas , a work attributed to Archimedes. [1]
Let A, D, E, and B be four points on a line in the plane, in that order, with AD = EB. Let O be the bisector of segment AB (and of DE). Draw semicircles above line AB with diameters AB, AD, and EB, and another semicircle below with diameter DE. A salinon is the figure bounded by these four semicircles. [2]
Archimedes introduced the salinon in his Book of Lemmas by applying Book II, Proposition 10 of Euclid's Elements. Archimedes noted that "the area of the figure bounded by the circumferences of all the semicircles [is] equal to the area of the circle on CF as diameter." [3]
Namely, if is the radius of large enclosing semicircle, and is the radius of the small central semicircle, then the area of the salinon is: [4]
Should points D and E converge with O, it would form an arbelos, another one of Archimedes' creations, with symmetry along the y-axis. [3]

Area is the measure of a region's size on a surface. The area of a plane region or plane area refers to the area of a shape or planar lamina, while surface area refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve or the volume of a solid . Two different regions may have the same area ; by synecdoche, "area" sometimes is used to refer to the region, as in a "polygonal area".

A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. The distance between any point of the circle and the centre is called the radius.

A sphere is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. Formally, a sphere is the set of points that are all at the same distance r from a given point in three-dimensional space. That given point is the centre of the sphere, and r is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians.

In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to a line containing the side opposite the vertex. This line containing the opposite side is called the extended base of the altitude. The intersection of the extended base and the altitude is called the foot of the altitude. The length of the altitude, often simply called "the altitude", is the distance between the extended base and the vertex. The process of drawing the altitude from the vertex to the foot is known as dropping the altitude at that vertex. It is a special case of orthogonal projection.

In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and the circumradius respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case.
The Method of Mechanical Theorems, also referred to as The Method, is one of the major surviving works of the ancient Greek polymath Archimedes. The Method takes the form of a letter from Archimedes to Eratosthenes, the chief librarian at the Library of Alexandria, and contains the first attested explicit use of indivisibles. The work was originally thought to be lost, but in 1906 was rediscovered in the celebrated Archimedes Palimpsest. The palimpsest includes Archimedes' account of the "mechanical method", so called because it relies on the center of weights of figures (centroid) and the law of the lever, which were demonstrated by Archimedes in On the Equilibrium of Planes.

In geometry, Thales's theorem states that if A, B, and C are distinct points on a circle where the line AC is a diameter, the angle ∠ ABC is a right angle. Thales's theorem is a special case of the inscribed angle theorem and is mentioned and proved as part of the 31st proposition in the third book of Euclid's Elements. It is generally attributed to Thales of Miletus, but it is sometimes attributed to Pythagoras.

In mathematics, a semicircle is a one-dimensional locus of points that forms half of a circle. It is a circular arc that measures 180°. It has only one line of symmetry.

A cylinder has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base.

In geometry, an arbelos is a plane region bounded by three semicircles with three apexes such that each corner of each semicircle is shared with one of the others (connected), all on the same side of a straight line that contains their diameters.
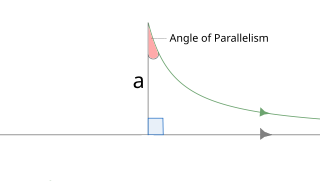
In hyperbolic geometry, angle of parallelism is the angle at the non-right angle vertex of a right hyperbolic triangle having two asymptotic parallel sides. The angle depends on the segment length a between the right angle and the vertex of the angle of parallelism.
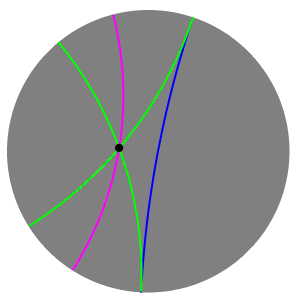
In hyperbolic geometry, two lines are said to be ultraparallel if they do not intersect and are not limiting parallel.

In geometry, the area enclosed by a circle of radius r is πr2. Here the Greek letter π represents the constant ratio of the circumference of any circle to its diameter, approximately equal to 3.14159.
Napoleon's problem is a compass construction problem. In it, a circle and its center are given. The challenge is to divide the circle into four equal arcs using only a compass. Napoleon was known to be an amateur mathematician, but it is not known if he either created or solved the problem. Napoleon's friend the Italian mathematician Lorenzo Mascheroni introduced the limitation of using only a compass into geometric constructions. But actually, the challenge above is easier than the real Napoleon's problem, consisting in finding the center of a given circle with compass alone. The following sections will describe solutions to three problems and proofs that they work.

In geometry, the Bankoff circle or Bankoff triplet circle is a certain Archimedean circle that can be constructed from an arbelos; an Archimedean circle is any circle with area equal to each of Archimedes' twin circles. The Bankoff circle was first constructed by Leon Bankoff in 1974.

In geometry, the twin circles are two special circles associated with an arbelos. An arbelos is determined by three collinear points A, B, and C, and is the curvilinear triangular region between the three semicircles that have AB, BC, and AC as their diameters. If the arbelos is partitioned into two smaller regions by a line segment through the middle point of A, B, and C, perpendicular to line ABC, then each of the two twin circles lies within one of these two regions, tangent to its two semicircular sides and to the splitting segment.

In geometry, Archimedes' quadruplets are four congruent circles associated with an arbelos. Introduced by Frank Power in the summer of 1998, each have the same area as Archimedes' twin circles, making them Archimedean circles.

In geometry, an Archimedean circle is any circle constructed from an arbelos that has the same radius as each of Archimedes' twin circles. If the arbelos is normed such that the diameter of its outer (largest) half circle has a length of 1 and r denotes the radiius of any of the inner half circles, then the radius ρ of such an Archimedean circle is given by

The Book of Lemmas or Book of Assumptions is a book attributed to Archimedes by Thābit ibn Qurra, though the authorship of the book is questionable. It consists of fifteen propositions (lemmas) on circles.

The quadratrix or trisectrix of Hippias is a curve which is created by a uniform motion. It is one of the oldest examples for a kinematic curve. Its discovery is attributed to the Greek sophist Hippias of Elis, who used it around 420 BC in an attempt to solve the angle trisection problem. Later around 350 BC Dinostratus used it in an attempt to solve the problem of squaring the circle.