Scaling pattern of occupancy

Last updated

In spatial ecology and macroecology, scaling pattern of occupancy (SPO), also known as the area-of-occupancy (AOO) is the way in which species distribution changes across spatial scales. In physical geography and image analysis, it is similar to the modifiable areal unit problem. Simon A. Levin (1992) [1] states that the problem of relating phenomena across scales is the central problem in biology and in all of science. Understanding the SPO is thus one central theme in ecology.

Contents

Pattern description

This pattern is often plotted as log-transformed grain (cell size) versus log-transformed occupancy. Kunin (1998) [2] presented a log-log linear SPO and suggested a fractal nature for species distributions. It has since been shown to follow a logistic shape, reflecting a percolation process. Furthermore, the SPO is closely related to the intraspecific occupancy-abundance relationship. For instance, if individuals are randomly distributed in space, the number of individuals in an α-size cell follows a Poisson distribution, with the occupancy being Pα = 1 − exp(−μα), where μ is the density. [3] Clearly, Pα in this Poisson model for randomly distributed individuals is also the SPO. Other probability distributions, such as the negative binomial distribution, can also be applied for describing the SPO and the occupancy-abundance relationship for non-randomly distributed individuals. [4]

Other occupancy-abundance models that can be used to describe the SPO includes Nachman's exponential model, [5] Hanski and Gyllenberg's metapopulation model, [6] He and Gaston's [7] improved negative binomial model by applying Taylor's power law between the mean and variance of species distribution, [8] and Hui and McGeoch's droopy-tail percolation model. [9] One important application of the SPO in ecology is to estimate species abundance based on presence-absence data, or occupancy alone. [10] This is appealing because obtaining presence-absence data is often cost-efficient. Using a dipswitch test consisting of 5 subtests and 15 criteria, Hui et al. [11] confirmed that using the SPO is robust and reliable for assemblage-scale regional abundance estimation. The other application of SPOs includes trends identification in populations, which is extremely valuable for biodiversity conservation. [12]

Explanation

Models providing explanations to the observed scaling pattern of occupancy include the fractal model, the cross-scale model and the Bayesian estimation model. The fractal model can be configured by dividing the landscape into quadrats of different sizes, [13] [14] or bisecting into grids with special width-to-length ratio (2:1), [15] [16] and yields the following SPO:

where D is the box-counting fractal dimension. If during each step a quadrat is divided into q sub-quadrats, we will find a constant portion (f) of sub-quadrats is also present in the fractal model, i.e. D = 2(1 + log ƒ/log q). Since this assumption that f is scale independent is not always the case in nature, [17] a more general form of ƒ can be assumed, ƒ = q−λ (λ is a constant), which yields the cross-scale model: [18]

The Bayesian estimation model follows a different way of thinking. Instead of providing the best-fit model as above, the occupancy at different scales can be estimated by Bayesian rule based on not only the occupancy but also the spatial autocorrelation at one specific scale. For the Bayesian estimation model, Hui et al. [19] provide the following formula to describe the SPO and join-count statistics of spatial autocorrelation:

where Ω = p(a)0 − q(a)0/+p(a)+ and  = p(a)0(1 − p(a)+2(2q(a)+/+ − 3) + p(a)+(q(a)+/+2 − 3)). p(a)+ is occupancy; q(a)+/+ is the conditional probability that a randomly chosen adjacent quadrat of an occupied quadrat is also occupied. The conditional probability q(a)0/+ = 1 − q(a)+/+ is the absence probability in a quadrate adjacent to an occupied one; a and 4a are the grains. The R-code of the Bayesian estimation model has been provided elsewhere. The key point of the Bayesian estimation model is that the scaling pattern of species distribution, measured by occupancy and spatial pattern, can be extrapolated across scales. Later on, Hui [20] provides the Bayesian estimation model for continuously changing scales:

where b, c, and h are constants. This SPO becomes the Poisson model when b = c = 1. In the same paper, the scaling pattern of join-count spatial autocorrelation and multi-species association (or co-occurrence) were also provided by the Bayesian model, suggesting that "the Bayesian model can grasp the statistical essence of species scaling patterns."

Implications for biological conservation

The probability of species extinction and ecosystem collapse increases rapidly as range size declines. In risk assessment protocols such as the IUCN Red List of Species or the IUCN Red List of Ecosystems, area of occupancy (AOO) is used as a standardized, complementary and widely applicable measure of risk spreading against spatially explicit threats. [21] [22]

Related Research Articles

In probability theory and statistics, Bayes' theorem, named after Thomas Bayes, describes the probability of an event, based on prior knowledge of conditions that might be related to the event. For example, if the risk of developing health problems is known to increase with age, Bayes' theorem allows the risk to an individual of a known age to be assessed more accurately by conditioning it relative to their age, rather than assuming that the individual is typical of the population as a whole.

Bayesian inference is a method of statistical inference in which Bayes' theorem is used to update the probability for a hypothesis as more evidence or information becomes available. Fundamentally, Bayesian inference uses prior knowledge, in the form of a prior distribution in order to estimate posterior probabilities. Bayesian inference is an important technique in statistics, and especially in mathematical statistics. Bayesian updating is particularly important in the dynamic analysis of a sequence of data. Bayesian inference has found application in a wide range of activities, including science, engineering, philosophy, medicine, sport, and law. In the philosophy of decision theory, Bayesian inference is closely related to subjective probability, often called "Bayesian probability".

Geostatistics is a branch of statistics focusing on spatial or spatiotemporal datasets. Developed originally to predict probability distributions of ore grades for mining operations, it is currently applied in diverse disciplines including petroleum geology, hydrogeology, hydrology, meteorology, oceanography, geochemistry, geometallurgy, geography, forestry, environmental control, landscape ecology, soil science, and agriculture. Geostatistics is applied in varied branches of geography, particularly those involving the spread of diseases (epidemiology), the practice of commerce and military planning (logistics), and the development of efficient spatial networks. Geostatistical algorithms are incorporated in many places, including geographic information systems (GIS).

<span class="mw-page-title-main">Metropolis–Hastings algorithm</span> Monte Carlo algorithm

In statistics and statistical physics, the Metropolis–Hastings algorithm is a Markov chain Monte Carlo (MCMC) method for obtaining a sequence of random samples from a probability distribution from which direct sampling is difficult. New samples are added to the sequence in two steps: first a new sample is proposed based on the previous sample, then the proposed sample is either added to the sequence or rejected depending on the value of the probability distribution at that point. The resulting sequence can be used to approximate the distribution or to compute an integral.

The principle of maximum entropy states that the probability distribution which best represents the current state of knowledge about a system is the one with largest entropy, in the context of precisely stated prior data.

<span class="mw-page-title-main">Unified neutral theory of biodiversity</span> Theory of evolutionary biology

The unified neutral theory of biodiversity and biogeography is a theory and the title of a monograph by ecologist Stephen P. Hubbell. It aims to explain the diversity and relative abundance of species in ecological communities. Like other neutral theories of ecology, Hubbell assumes that the differences between members of an ecological community of trophically similar species are "neutral", or irrelevant to their success. This implies that niche differences do not influence abundance and the abundance of each species follows a random walk. The theory has sparked controversy, and some authors consider it a more complex version of other null models that fit the data better.

Mark and recapture is a method commonly used in ecology to estimate an animal population's size where it is impractical to count every individual. A portion of the population is captured, marked, and released. Later, another portion will be captured and the number of marked individuals within the sample is counted. Since the number of marked individuals within the second sample should be proportional to the number of marked individuals in the whole population, an estimate of the total population size can be obtained by dividing the number of marked individuals by the proportion of marked individuals in the second sample. The method assumes, rightly or wrongly, that the probability of capture is the same for all individuals. Other names for this method, or closely related methods, include capture-recapture, capture-mark-recapture, mark-recapture, sight-resight, mark-release-recapture, multiple systems estimation, band recovery, the Petersen method, and the Lincoln method.

Spatial ecology studies the ultimate distributional or spatial unit occupied by a species. In a particular habitat shared by several species, each of the species is usually confined to its own microhabitat or spatial niche because two species in the same general territory cannot usually occupy the same ecological niche for any significant length of time.

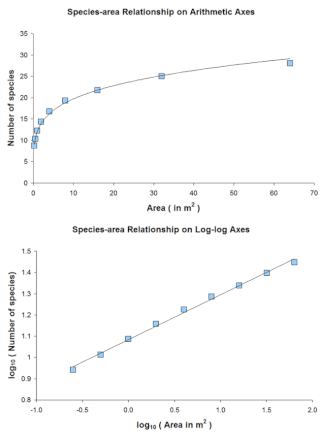
<span class="mw-page-title-main">Species–area relationship</span> Relationship between the size of an area or habitat and the number of species it can support

The species–area relationship or species–area curve describes the relationship between the area of a habitat, or of part of a habitat, and the number of species found within that area. Larger areas tend to contain larger numbers of species, and empirically, the relative numbers seem to follow systematic mathematical relationships. The species–area relationship is usually constructed for a single type of organism, such as all vascular plants or all species of a specific trophic level within a particular site. It is rarely if ever, constructed for all types of organisms if simply because of the prodigious data requirements. It is related but not identical to the species discovery curve.

<span class="mw-page-title-main">Credible interval</span> Concept in Bayesian statistics

In Bayesian statistics, a credible interval is an interval used to characterize a probability distribution. It is defined such that an unobserved parameter value has a particular probability to fall within it. For example, in an experiment that determines the distribution of possible values of the parameter , if the probability that lies between 35 and 45 is , then is a 95% credible interval.

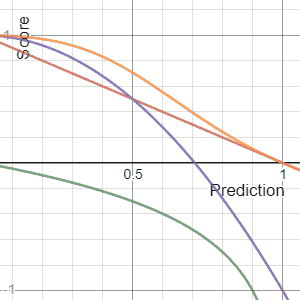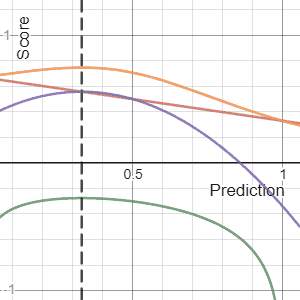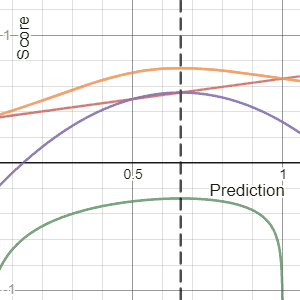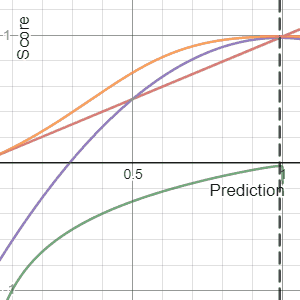
<span class="mw-page-title-main">Scoring rule</span> Measure for evaluating probabilistic forecasts

In decision theory, a scoring rule provides evaluation metrics for probabilistic predictions or forecasts. While "regular" loss functions assign a goodness-of-fit score to a predicted value and an observed value, scoring rules assign such a score to a predicted probability distribution and an observed value. On the other hand, a scoring function provides a summary measure for the evaluation of point predictions, i.e. one predicts a property or functional , like the expectation or the median.

<span class="mw-page-title-main">Multifractal system</span> System with multiple fractal dimensions

A multifractal system is a generalization of a fractal system in which a single exponent is not enough to describe its dynamics; instead, a continuous spectrum of exponents is needed.

Approximate Bayesian computation (ABC) constitutes a class of computational methods rooted in Bayesian statistics that can be used to estimate the posterior distributions of model parameters.

In ecology, the occupancy–abundance (O–A) relationship is the relationship between the abundance of species and the size of their ranges within a region. This relationship is perhaps one of the most well-documented relationships in macroecology, and applies both intra- and interspecifically. In most cases, the O–A relationship is a positive relationship. Although an O–A relationship would be expected, given that a species colonizing a region must pass through the origin and could reach some theoretical maximum abundance and distribution, the relationship described here is somewhat more substantial, in that observed changes in range are associated with greater-than-proportional changes in abundance. Although this relationship appears to be pervasive, and has important implications for the conservation of endangered species, the mechanism(s) underlying it remain poorly understood.

Mechanistic models for niche apportionment are biological models used to explain relative species abundance distributions. These niche apportionment models describe how species break up resource pool in multi-dimensional space, determining the distribution of abundances of individuals among species. The relative abundances of species are usually expressed as a Whittaker plot, or rank abundance plot, where species are ranked by number of individuals on the x-axis, plotted against the log relative abundance of each species on the y-axis. The relative abundance can be measured as the relative number of individuals within species or the relative biomass of individuals within species.

In macroecology and community ecology, an occupancy frequency distribution (OFD) is the distribution of the numbers of species occupying different numbers of areas. It was first reported in 1918 by the Danish botanist Christen C. Raunkiær in his study on plant communities. The OFD is also known as the species-range size distribution in literature.

Taylor's power law is an empirical law in ecology that relates the variance of the number of individuals of a species per unit area of habitat to the corresponding mean by a power law relationship. It is named after the ecologist who first proposed it in 1961, Lionel Roy Taylor (1924–2007). Taylor's original name for this relationship was the law of the mean. The name Taylor's law was coined by Southwood in 1966.

In ecology, plot sampling is a widely used method of abundance estimation in which specific areas, or plots, are selected from within a survey region and sampled. This approach allows scientists to make population estimates using statistical techniques such as the Horvitz–Thompson estimator. Plot sampling is generally effective when it can be assumed that each survey will identify all of the animals in the sampled area, and that the animals will be distributed uniformly and independently.

In probability theory and statistics, the discrete Weibull distribution is the discrete variant of the Weibull distribution. The Discrete Weibull Distribution, first introduced by Toshio Nakagawa and Shunji Osaki, is a discrete analog of the continuous Weibull distribution, predominantly used in reliability engineering. It is particularly applicable for modeling failure data measured in discrete units like cycles or shocks. This distribution provides a versatile tool for analyzing scenarios where the timing of events is counted in distinct intervals, making it distinctively useful in fields that deal with discrete data patterns and reliability analysis.

References

  1. ↑ Levin, SA. 1992. The problem of pattern and scale in ecology. Ecology, 73, 1943–1967.
  2. ↑ Kunin, WE. 1998. Extrapolating species abundance across spatial scales. Science, 281: 1513–1515.
  3. ↑ Wright, D.H. 1991. Correlations between incidence and abundance are expected by chance. Journal of Biogeography, 18: 463–466.
  4. ↑ He, F., Gaston, K.J. 2000. Estimating species abundance from occurrence. American Naturalist, 156: 553–559.
  5. ↑ Nachman, G. 1981. A mathematical model of the functional relationship between density and spatial distribution of a population. Journal of Animal Ecology, 50: 453–460.
  6. ↑ Hanski, I., Gyllenberg, M. 1997. Uniting two general patterns in the distribution of species. Science, 284: 334–336.
  7. ↑ He, F., Gaston, K.J. 2003. Occupancy, spatial variance, and the abundance of species. American Naturalist, 162: 366–375.
  8. ↑ Taylor, L.R. 1961. Aggregation, variance and the mean. Nature, 189: 732–735.
  9. ↑ Hui, C., McGeoch, MA. 2007. Capturing the "droopy tail" in the occupancy-abundance relationship. Ecoscience, 14: 103–108.
  10. ↑ Hartley, S., Kunin, WE. 2003. Scale dependence of rarity, extinction risk, and conservation priority. Conservation Biology, 17: 1559–1570.
  11. ↑ Hui, C., McGeoch, M.A., Reyers, B., le Roux, P.C., Greve, M., Chown, S.L. 2009. Extrapolating population size from the occupancy-abundance relationship and the scaling pattern of occupancy. Ecological Applications, 19: 2038–2048.
  12. ↑ Wilson, RJ., Thomas, CD., Fox, R., Roy, RD., Kunin, WE. 2004. Spatial patterns in species distributions reveals biodiversity change. Nature, 432: 393–396.
  13. ↑ Hasting, H.M. & Sugihara, G. (1993) Fractals: a User's Guide for the Natural Sciences. Oxford University Press.
  14. ↑ Kunin, WE. 1998. Extrapolating species abundance across spatial scales. Science, 281: 1513–1515.
  15. ↑ Harte, J., Kinzig, A.P. & Green, J. (1999) Self-similarity in the distribution and abundance of species. Science 294, 334–336.
  16. ↑ Hui, C. & McGeoch, M.A. (2007) A self-similarity model for occupancy frequency distributions. Theoretical Population Biology 71: 61–70.
  17. ↑ Hui, C. & McGeoch, M.A. (2007) Modeling species distributions by breaking the assumption of self-similarity. Oikos 116: 2097–2107.
  18. ↑ Lennon, J.J., Kunin, W.E., Hartley, S. & Gaston, K.J. (2007) Species distribution patterns, diversity scaling and testing for fractals in southern African birds. In: Scaling Biology (D. Storch, P.A. Marquet & J.H. Brown, eds.), pp. 51–76. Cambridge University Press.
  19. ↑ Hui, C., McGeoch, M.A. & Warren, M. (2006) A spatially explicitly approach to estimating species occupancy and spatial correlation. Journal of Animal Ecology 75: 140–147.
  20. ↑ Hui, C. (2009) On the scaling patterns of species spatial distribution and association. Journal of Theoretical Biology 261: 481–487.
  21. ↑ Murray, Nicholas J.; Keith, David A.; Bland, Lucie M.; Nicholson, Emily; Regan, Tracey J.; Rodríguez6,7,8, Jon Paul; Bedward, Michael (2017). "The use of range size to assess risks to biodiversity from stochastic threats". Diversity and Distributions. 23 (5): 474–483. Bibcode:2017DivDi..23..474M. doi: 10.1111/ddi.12533 . hdl: 10536/DRO/DU:30091065 .{{cite journal}}: CS1 maint: multiple names: authors list (link) CS1 maint: numeric names: authors list (link)
  22. ↑ Murray, Nicholas (2017). "Global 10 x 10-km grids suitable for use in IUCN Red List of Ecosystems assessments (vector and raster format)". Figshare. doi:10.6084/m9.figshare.4653439.v1.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.