In physics, metastability is a stable state of a dynamical system other than the system's state of least energy. A ball resting in a hollow on a slope is a simple example of metastability. If the ball is only slightly pushed, it will settle back into its hollow, but a stronger push may start the ball rolling down the slope. Bowling pins show similar metastability by either merely wobbling for a moment or tipping over completely. A common example of metastability in science is isomerisation. Higher energy isomers are long lived because they are prevented from rearranging to their preferred ground state by barriers in the potential energy.
In the physical sciences, a phase is a region of space, throughout which all physical properties of a material are essentially uniform. Examples of physical properties include density, index of refraction, magnetization and chemical composition. A simple description is that a phase is a region of material that is chemically uniform, physically distinct, and (often) mechanically separable. In a system consisting of ice and water in a glass jar, the ice cubes are one phase, the water is a second phase, and the humid air is a third phase over the ice and water. The glass of the jar is another separate phase.
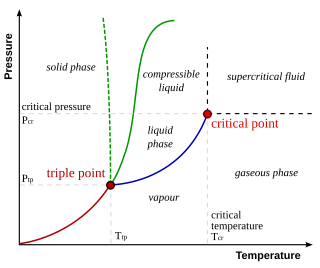
In thermodynamics, the triple point of a substance is the temperature and pressure at which the three phases of that substance coexist in thermodynamic equilibrium. It is that temperature and pressure at which the sublimation curve, fusion curve and the vaporisation curve meet. For example, the triple point of mercury occurs at a temperature of −38.83440 °C (−37.90192 °F) and a pressure of 0.165 mPa.
Le Chatelier's principle, also called Chatelier's principle, is a principle of chemistry used to predict the effect of a change in conditions on chemical equilibria. The principle is named after French chemist Henry Louis Le Chatelier, and sometimes also credited to Karl Ferdinand Braun, who discovered it independently. It can be stated as:
When any system at equilibrium for a long period of time is subjected to a change in concentration, temperature, volume, or pressure, (1) the system changes to a new equilibrium, and (2) this change partly counteracts the applied change.
A phase diagram in physical chemistry, engineering, mineralogy, and materials science is a type of chart used to show conditions at which thermodynamically distinct phases occur and coexist at equilibrium.
In dynamical system theory, a phase space is a space in which all possible states of a system are represented, with each possible state corresponding to one unique point in the phase space. For mechanical systems, the phase space usually consists of all possible values of position and momentum variables. The concept of phase space was developed in the late 19th century by Ludwig Boltzmann, Henri Poincaré, and Josiah Willard Gibbs.
The phase rule is a general principle governing "pVT systems" in thermodynamic equilibrium, whose states are completely described by the variables pressure (p), volume (V) and temperature (T). If F is the number of degrees of freedom, C is the number of components and P is the number of phases, then
In economics, an Edgeworth box, sometimes referred to as an Edgeworth-Bowley box, is a graphical representation of a market with just two commodities, X and Y, and two consumers. The dimensions of the box are the total quantities Ωx and Ωy of the two goods.
In thermodynamics, a critical point is the end point of a phase equilibrium curve. The most prominent example is the liquid–vapor critical point, the end point of the pressure–temperature curve that designates conditions under which a liquid and its vapor can coexist. At higher temperatures, the gas cannot be liquefied by pressure alone. At the critical point, defined by a critical temperatureTc and a critical pressurepc, phase boundaries vanish. Other examples include the liquid–liquid critical points in mixtures.
In electrochemistry, and more generally in solution chemistry, a Pourbaix diagram, also known as a potential/pH diagram, EH–pH diagram or a pE/pH diagram, is a plot of possible thermodynamically stable phases of an aqueous electrochemical system. Boundaries (50 %/50 %) between the predominant chemical species are represented by lines. As such a Pourbaix diagram can be read much like a standard phase diagram with a different set of axes. Similarly to phase diagrams, they do not allow for reaction rate or kinetic effects. Beside potential and pH, the equilibrium concentrations are also dependent upon, e.g., temperature, pressure, and concentration. Pourbaix diagrams are commonly given at room temperature, atmospheric pressure, and molar concentrations of 10−6 and changing any of these parameters will yield a different diagram.
An Ellingham diagram is a graph showing the temperature dependence of the stability of compounds. This analysis is usually used to evaluate the ease of reduction of metal oxides and sulfides. These diagrams were first constructed by Harold Ellingham in 1944. In metallurgy, the Ellingham diagram is used to predict the equilibrium temperature between a metal, its oxide, and oxygen — and by extension, reactions of a metal with sulfur, nitrogen, and other non-metals. The diagrams are useful in predicting the conditions under which an ore will be reduced to its metal. The analysis is thermodynamic in nature and ignores reaction kinetics. Thus, processes that are predicted to be favourable by the Ellingham diagram can still be slow.
Hammond's postulate, is a hypothesis in physical organic chemistry which describes the geometric structure of the transition state in an organic chemical reaction. First proposed by George Hammond in 1955, the postulate states that:
If two states, as, for example, a transition state and an unstable intermediate, occur consecutively during a reaction process and have nearly the same energy content, their interconversion will involve only a small reorganization of the molecular structures.
Thermodynamic databases contain information about thermodynamic properties for substances, the most important being enthalpy, entropy, and Gibbs free energy. Numerical values of these thermodynamic properties are collected as tables or are calculated from thermodynamic datafiles. Data is expressed as temperature-dependent values for one mole of substance at the standard pressure of 101.325 kPa, or 100 kPa. Unfortunately, both of these definitions for the standard condition for pressure are in use.
For a chemical reaction or process an energy profile is a theoretical representation of a single energetic pathway, along the reaction coordinate, as the reactants are transformed into products. Reaction coordinate diagrams are derived from the corresponding potential energy surface (PES), which are used in computational chemistry to model chemical reactions by relating the energy of a molecule(s) to its structure. The reaction coordinate is a parametric curve that follows the pathway of a reaction and indicates the progress of a reaction.
In chemistry, chemical stability is the thermodynamic stability of a chemical system.
George Simms Hammond was an American scientist and theoretical chemist who developed "Hammond's postulate", and fathered organic photochemistry,–the general theory of the geometric structure of the transition state in an organic chemical reaction. Hammond's research is also known for its influence on the philosophy of science. His research garnered him the Norris Award in 1968, the Priestley Medal in 1976, the National Medal of Science in 1994, and the Othmer Gold Medal in 2003. He served as the executive chairman of the Allied Chemical Corporation from 1979 to 1989.
In thermodynamics, the limit of local stability with respect to small fluctuations is clearly defined by the condition that the second derivative of Gibbs free energy is zero. The locus of these points is known as the spinodal curve. For compositions within this curve, infinitesimally small fluctuations in composition and density will lead to phase separation via spinodal decomposition. Outside of the curve, the solution will be at least metastable with respect to fluctuations. In other words, outside the spinodal curve some careful process may obtain a single phase system. Inside it, only processes far from thermodynamic equilibrium, such as physical vapor deposition, will enable one to prepare single phase compositions. The local points of coexisting compositions, defined by the common tangent construction, are known as a binodal (coexistence) curve, which denotes the minimum-energy equilibrium state of the system. Increasing temperature results in a decreasing difference between mixing entropy and mixing enthalpy, and thus the coexisting compositions come closer. The binodal curve forms the basis for the miscibility gap in a phase diagram. The free energy of mixing changes with temperature and concentration, and the binodal and spinodal meet at the critical or consolute temperature and composition.
Unimolecular ion decomposition is the fragmentation of a gas phase ion in a reaction with a molecularity of one. Ions with sufficient internal energy may fragment in a mass spectrometer, which in some cases may degrade the mass spectrometer performance, but in other cases, such as tandem mass spectrometry, the fragmentation can reveal information about the structure of the ion.
Chemical reaction network theory is an area of applied mathematics that attempts to model the behaviour of real-world chemical systems. Since its foundation in the 1960s, it has attracted a growing research community, mainly due to its applications in biochemistry and theoretical chemistry. It has also attracted interest from pure mathematicians due to the interesting problems that arise from the mathematical structures involved.
In thermodynamics, explosive boiling or phase explosion is a method whereby a superheated metastable liquid undergoes an explosive liquid-vapor phase transition into a stable two-phase state because of a massive homogeneous nucleation of vapor bubbles. This concept was pioneered by M. M. Martynyuk in 1976 and then later advanced by Fucke and Seydel.
