Schwarz function

Last updated November 01, 2022

The Schwarz function of a curve in the complex plane is an analytic function which maps the points of the curve to their complex conjugates. It can be used to generalize the Schwarz reflection principle to reflection across arbitrary analytic curves, not just across the real axis.

The Schwarz function exists for analytic curves. More precisely, for every non-singular, analytic Jordan arc $\Gamma$ in the complex plane, there is an open neighborhood $\Omega$ of $\Gamma$ and a unique analytic function $S$ on $\Omega$ such that $S(z)={\overline {z}}$ for every $z\in \Gamma$ .^[1]

The "Schwarz function" was named by Philip J. Davis and Henry O. Pollak (1958) in honor of Hermann Schwarz,^[2]^[3] who introduced the Schwarz reflection principle for analytic curves in 1870.^[4] However, the Schwarz function does not explicitly appear in Schwarz's works.^[5]

Examples

The unit circle is described by the equation $|z|^{2}=1$ , or ${\overline {z}}=1/z$ . Thus, the Schwarz function of the unit circle is $S(z)=1/z$ .

A more complicated example is an ellipse defined by $(x/a)^{2}+(y/b)^{2}=1$ . The Schwarz function can be found by substituting $\textstyle x={\frac {z+{\overline {z}}}{2}}$ and $\textstyle y={\frac {z-{\overline {z}}}{2i}}$ and solving for ${\overline {z}}$ . The result is:^[6]

S(z)={\frac {1}{a^{2}-b^{2}}}\left((a^{2}+b^{2})z-2ab{\sqrt {z^{2}+b^{2}-a^{2}}}\right)

.

This is analytic on the complex plane minus a branch cut along the line segment between the foci $\pm {\sqrt {a^{2}-b^{2}}}$ .

Related Research Articles

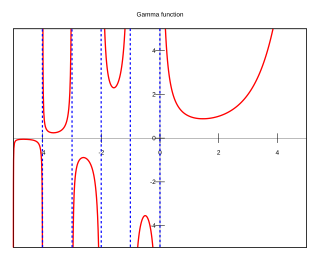
In mathematics, the gamma function is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer $n$ ,

In mathematics, a holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighbourhood of each point in a domain in complex coordinate space $C n$ . The existence of a complex derivative in a neighbourhood is a very strong condition: it implies that a holomorphic function is infinitely differentiable and locally equal to its own Taylor series (analytic). Holomorphic functions are the central objects of study in complex analysis.

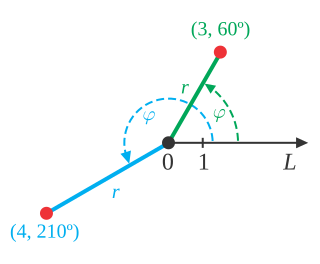
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point is called the pole, and the ray from the pole in the reference direction is the polar axis. The distance from the pole is called the radial coordinate, radial distance or simply radius, and the angle is called the angular coordinate, polar angle, or azimuth. Angles in polar notation are generally expressed in either degrees or radians.

The propagation constant of a sinusoidal electromagnetic wave is a measure of the change undergone by the amplitude and phase of the wave as it propagates in a given direction. The quantity being measured can be the voltage, the current in a circuit, or a field vector such as electric field strength or flux density. The propagation constant itself measures the change per unit length, but it is otherwise dimensionless. In the context of two-port networks and their cascades, propagation constant measures the change undergone by the source quantity as it propagates from one port to the next.

In mathematics, the Cauchy integral theorem in complex analysis, named after Augustin-Louis Cauchy, is an important statement about line integrals for holomorphic functions in the complex plane. Essentially, it says that if $is holomorphic in a simply connected domain Ω, then for any simply closed contour in Ω, that contour integral is zero.$

In mathematics, the winding number or winding index of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point, i.e., the curve's number of turns. The winding number depends on the orientation of the curve, and it is negative if the curve travels around the point clockwise.

In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space $under the operation of composition.$

In vector calculus, Green's theorem relates a line integral around a simple closed curve $C$ to a double integral over the plane region $D$ bounded by $C$ . It is the two-dimensional special case of Stokes' theorem.

In quantum field theory, the Dirac spinor is the spinor that describes all known fundamental particles that are fermions, with the possible exception of neutrinos. It appears in the plane-wave solution to the Dirac equation, and is a certain combination of two Weyl spinors, specifically, a bispinor that transforms "spinorially" under the action of the Lorentz group.

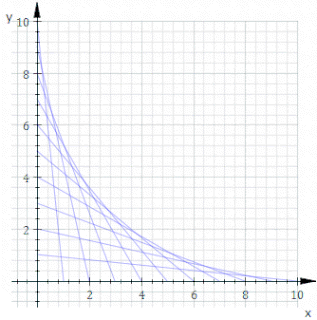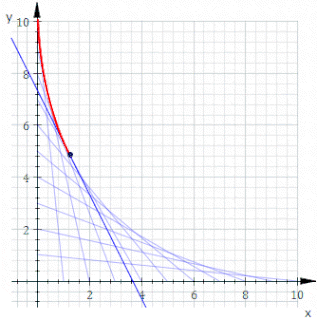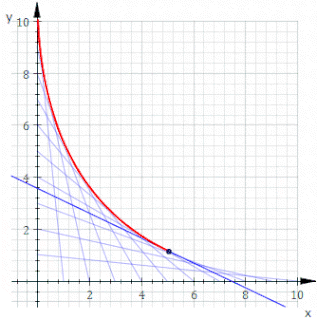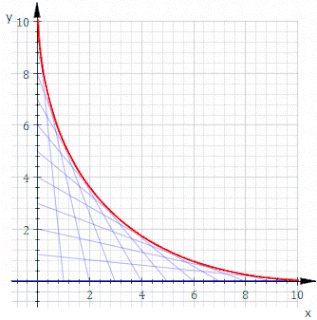
<span class="mw-page-title-main">Envelope (mathematics)</span> Family of curves in geometry

In geometry, an envelope of a planar family of curves is a curve that is tangent to each member of the family at some point, and these points of tangency together form the whole envelope. Classically, a point on the envelope can be thought of as the intersection of two "infinitesimally adjacent" curves, meaning the limit of intersections of nearby curves. This idea can be generalized to an envelope of surfaces in space, and so on to higher dimensions.

In physics, the Hamilton–Jacobi equation, named after William Rowan Hamilton and Carl Gustav Jacob Jacobi, is an alternative formulation of classical mechanics, equivalent to other formulations such as Newton's laws of motion, Lagrangian mechanics and Hamiltonian mechanics. The Hamilton–Jacobi equation is particularly useful in identifying conserved quantities for mechanical systems, which may be possible even when the mechanical problem itself cannot be solved completely.

In optics, an ultrashort pulse, also known as an ultrafast event, is an electromagnetic pulse whose time duration is of the order of a picosecond or less. Such pulses have a broadband optical spectrum, and can be created by mode-locked oscillators. Amplification of ultrashort pulses almost always requires the technique of chirped pulse amplification, in order to avoid damage to the gain medium of the amplifier.

In mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry or Riemann surfaces.

In mathematics, Maass forms or Maass wave forms are studied in the theory of automorphic forms. Maass forms are complex-valued smooth functions of the upper half plane, which transform in a similar way under the operation of a discrete subgroup $of as modular forms. They are Eigenforms of the hyperbolic Laplace Operator defined on and satisfy certain growth conditions at the cusps of a fundamental domain of . In contrast to the modular forms the Maass forms need not be holomorphic. They were studied first by Hans Maass in 1949.$

In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve. The terms path integral, curve integral, and curvilinear integral are also used; contour integral is used as well, although that is typically reserved for line integrals in the complex plane.

The narrow escape problem is a ubiquitous problem in biology, biophysics and cellular biology.

In mathematics, the Beltrami equation, named after Eugenio Beltrami, is the partial differential equation

In mathematics, Ramanujan's Master Theorem is a technique that provides an analytic expression for the Mellin transform of an analytic function.

In mathematics, differential forms on a Riemann surface are an important special case of the general theory of differential forms on smooth manifolds, distinguished by the fact that the conformal structure on the Riemann surface intrinsically defines a Hodge star operator on 1-forms without specifying a Riemannian metric. This allows the use of Hilbert space techniques for studying function theory on the Riemann surface and in particular for the construction of harmonic and holomorphic differentials with prescribed singularities. These methods were first used by Hilbert (1909) in his variational approach to the Dirichlet principle, making rigorous the arguments proposed by Riemann. Later Weyl (1940) found a direct approach using his method of orthogonal projection, a precursor of the modern theory of elliptic differential operators and Sobolev spaces. These techniques were originally applied to prove the uniformization theorem and its generalization to planar Riemann surfaces. Later they supplied the analytic foundations for the harmonic integrals of Hodge (1940). This article covers general results on differential forms on a Riemann surface that do not rely on any choice of Riemannian structure.

In complex analysis, the Schwarz triangle function or Schwarz s-function is a function that conformally maps the upper half plane to a triangle in the upper half plane having lines or circular arcs for edges. The target triangle is not necessarily a Schwarz triangle, although that is the most mathematically interesting case. When that triangle is a non-overlapping Schwarz triangle, i.e. a Möbius triangle, the inverse of the Schwarz triangle function is a single-valued automorphic function for that triangle's triangle group. More specifically, it is a modular function.

References

↑ Shapiro 1992 , p. 3
↑ Davis, Phillip; Pollak, Henry (January 1958). "On the Analytic Continuation of Mapping Functions" (PDF). Transactions of the American Mathematical Society. 87 (1): 198–225. doi: 10.2307/1993097 . JSTOR 1993097.
↑ Needham 1997 , p. 255
↑ Schwarz, H.A. (1870). "Ueber die Integration der paritellen Differentialgleichung $\textstyle {\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}=0$ unter vorgeschriebenen Grenz- und Unstetigkeitsbedingungen". Monatsberichte der Königlichen Preussische Akademie des Wissenschaften zu Berlin: 767–795. Reprinted in: Schwarz, H.A. (1890). Gesammelte Mathematische Abhandlungen. Vol. II. pp. 144–171.
↑ Shapiro 1992 , p. 2
↑ Needham 1997 , p. 256

Davis, Philip J. (1974). The Schwarz function and its applications. Carus Monographs 17. Mathematical Association of America. ISBN 978-0-883-85017-6. OCLC 912405492.
Needham, Tristan (1997). Visual Complex Analysis. Clarendon Press. ISBN 978-0-19-853447-1.
Shapiro, Harold S. (1992-03-18). The Schwarz Function and Its Generalization to Higher Dimensions. John Wiley & Sons. ISBN 978-0-471-57127-8. OCLC 924755133.

This mathematics-related article is a stub. You can help Wikipedia by expanding it.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Shapiro 1992 , p. 3

[Davis-Pollak-2] Davis, Phillip; Pollak, Henry (January 1958). "On the Analytic Continuation of Mapping Functions" (PDF). Transactions of the American Mathematical Society. 87 (1): 198–225. doi: 10.2307/1993097 . JSTOR 1993097.

[3] Needham 1997 , p. 255

[4] Schwarz, H.A. (1870). "Ueber die Integration der paritellen Differentialgleichung $\textstyle {\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}=0$ unter vorgeschriebenen Grenz- und Unstetigkeitsbedingungen". Monatsberichte der Königlichen Preussische Akademie des Wissenschaften zu Berlin: 767–795. Reprinted in: Schwarz, H.A. (1890). Gesammelte Mathematische Abhandlungen. Vol. II. pp. 144–171.

[5] Shapiro 1992 , p. 2

[6] Needham 1997 , p. 256

[1]

[2]

[3]

[4]

[5]

[6]