Bra–ket notation, also called Dirac notation, is a notation for linear algebra and linear operators on complex vector spaces together with their dual space both in the finite-dimensional and infinite-dimensional case. It is specifically designed to ease the types of calculations that frequently come up in quantum mechanics. Its use in quantum mechanics is quite widespread.

In theoretical physics, a Feynman diagram is a pictorial representation of the mathematical expressions describing the behavior and interaction of subatomic particles. The scheme is named after American physicist Richard Feynman, who introduced the diagrams in 1948. The interaction of subatomic particles can be complex and difficult to understand; Feynman diagrams give a simple visualization of what would otherwise be an arcane and abstract formula. According to David Kaiser, "Since the middle of the 20th century, theoretical physicists have increasingly turned to this tool to help them undertake critical calculations. Feynman diagrams have revolutionized nearly every aspect of theoretical physics." While the diagrams are applied primarily to quantum field theory, they can also be used in other areas of physics, such as solid-state theory. Frank Wilczek wrote that the calculations that won him the 2004 Nobel Prize in Physics "would have been literally unthinkable without Feynman diagrams, as would [Wilczek's] calculations that established a route to production and observation of the Higgs particle."

The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after Erwin Schrödinger, who postulated the equation in 1925 and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933.

In quantum physics, a wave function is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters ψ and Ψ. Wave functions are complex-valued. For example, a wave function might assign a complex number to each point in a region of space. The Born rule provides the means to turn these complex probability amplitudes into actual probabilities. In one common form, it says that the squared modulus of a wave function that depends upon position is the probability density of measuring a particle as being at a given place. The integral of a wavefunction's squared modulus over all the system's degrees of freedom must be equal to 1, a condition called normalization. Since the wave function is complex-valued, only its relative phase and relative magnitude can be measured; its value does not, in isolation, tell anything about the magnitudes or directions of measurable observables. One has to apply quantum operators, whose eigenvalues correspond to sets of possible results of measurements, to the wave function ψ and calculate the statistical distributions for measurable quantities.

Quantum decoherence is the loss of quantum coherence, the process in which a system's behaviour changes from that which can be explained by quantum mechanics to that which can be explained by classical mechanics. Beginning out of attempts to extend the understanding of quantum mechanics, the theory has developed in several directions and experimental studies have confirmed some of the key issues. Quantum computing relies on quantum coherence and is the primary practical applications of the concept.
In physics, the S-matrix or scattering matrix relates the initial state and the final state of a physical system undergoing a scattering process. It is used in quantum mechanics, scattering theory and quantum field theory (QFT).

The Schwinger–Dyson equations (SDEs) or Dyson–Schwinger equations, named after Julian Schwinger and Freeman Dyson, are general relations between correlation functions in quantum field theories (QFTs). They are also referred to as the Euler–Lagrange equations of quantum field theories, since they are the equations of motion corresponding to the Green's function. They form a set of infinitely many functional differential equations, all coupled to each other, sometimes referred to as the infinite tower of SDEs.
Møller–Plesset perturbation theory (MP) is one of several quantum chemistry post-Hartree–Fock ab initio methods in the field of computational chemistry. It improves on the Hartree–Fock method by adding electron correlation effects by means of Rayleigh–Schrödinger perturbation theory (RS-PT), usually to second (MP2), third (MP3) or fourth (MP4) order. Its main idea was published as early as 1934 by Christian Møller and Milton S. Plesset.
Time-dependent density-functional theory (TDDFT) is a quantum mechanical theory used in physics and chemistry to investigate the properties and dynamics of many-body systems in the presence of time-dependent potentials, such as electric or magnetic fields. The effect of such fields on molecules and solids can be studied with TDDFT to extract features like excitation energies, frequency-dependent response properties, and photoabsorption spectra.
In mathematical physics, some approaches to quantum field theory are more popular than others. For historical reasons, the Schrödinger representation is less favored than Fock space methods. In the early days of quantum field theory, maintaining symmetries such as Lorentz invariance, displaying them manifestly, and proving renormalisation were of paramount importance. The Schrödinger representation is not manifestly Lorentz invariant and its renormalisability was only shown as recently as the 1980s by Kurt Symanzik (1981).
The Lippmann–Schwinger equation is one of the most used equations to describe particle collisions – or, more precisely, scattering – in quantum mechanics. It may be used in scattering of molecules, atoms, neutrons, photons or any other particles and is important mainly in atomic, molecular, and optical physics, nuclear physics and particle physics, but also for seismic scattering problems in geophysics. It relates the scattered wave function with the interaction that produces the scattering and therefore allows calculation of the relevant experimental parameters.
The theoretical and experimental justification for the Schrödinger equation motivates the discovery of the Schrödinger equation, the equation that describes the dynamics of nonrelativistic particles. The motivation uses photons, which are relativistic particles with dynamics described by Maxwell's equations, as an analogue for all types of particles.
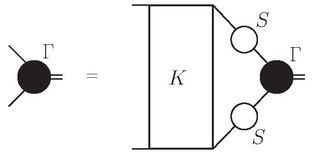
The Bethe–Salpeter equation describes the bound states of a two-body (particles) quantum field theoretical system in a relativistically covariant formalism. The equation was first published in 1950 at the end of a paper by Yoichiro Nambu, but without derivation.
In quantum physics, a quantum state is a mathematical entity that embodies the knowledge of a quantum system. Quantum mechanics specifies the construction, evolution, and measurement of a quantum state. The result is a quantum-mechanical prediction for the system represented by the state. Knowledge of the quantum state, and the quantum mechanical rules for the system's evolution in time, exhausts all that can be known about a quantum system.
This is a glossary for the terminology often encountered in undergraduate quantum mechanics courses.
The Born series is the expansion of different scattering quantities in quantum scattering theory in the powers of the interaction potential . It is closely related to Born approximation, which is the first order term of the Born series. The series can formally be understood as power series introducing the coupling constant by substitution . The speed of convergence and radius of convergence of the Born series are related to eigenvalues of the operator . In general the first few terms of the Born series are good approximation to the expanded quantity for "weak" interaction and large collision energy.
The projector augmented wave method (PAW) is a technique used in ab initio electronic structure calculations. It is a generalization of the pseudopotential and linear augmented-plane-wave methods, and allows for density functional theory calculations to be performed with greater computational efficiency.
In quantum mechanics, the variational method is one way of finding approximations to the lowest energy eigenstate or ground state, and some excited states. This allows calculating approximate wavefunctions such as molecular orbitals. The basis for this method is the variational principle.
The method of continued fractions is a method developed specifically for solution of integral equations of quantum scattering theory like Lippmann–Schwinger equation or Faddeev equations. It was invented by Horáček and Sasakawa in 1983. The goal of the method is to solve the integral equation
Multiple scattering theory (MST) is the mathematical formalism that is used to describe the propagation of a wave through a collection of scatterers. Examples are acoustical waves traveling through porous media, light scattering from water droplets in a cloud, or x-rays scattering from a crystal. A more recent application is to the propagation of quantum matter waves like electrons or neutrons through a solid.

















