Simple shear is a deformation in which parallel planes in a material remain parallel and maintain a constant distance, while translating relative to each other.
Simple shear is a deformation in which parallel planes in a material remain parallel and maintain a constant distance, while translating relative to each other.
In fluid mechanics, simple shear is a special case of deformation where only one component of velocity vectors has a non-zero value:
And the gradient of velocity is constant and perpendicular to the velocity itself:
where is the shear rate and:
The displacement gradient tensor Γ for this deformation has only one nonzero term:
Simple shear with the rate is the combination of pure shear strain with the rate of 1/2 and rotation with the rate of 1/2:
The mathematical model representing simple shear is a shear mapping restricted to the physical limits. It is an elementary linear transformation represented by a matrix. The model may represent laminar flow velocity at varying depths of a long channel with constant cross-section. Limited shear deformation is also used in vibration control, for instance base isolation of buildings for limiting earthquake damage.
In solid mechanics, a simple shear deformation is defined as an isochoric plane deformation in which there are a set of line elements with a given reference orientation that do not change length and orientation during the deformation. [1] This deformation is differentiated from a pure shear by virtue of the presence of a rigid rotation of the material. [2] [3] When rubber deforms under simple shear, its stress-strain behavior is approximately linear. [4] A rod under torsion is a practical example for a body under simple shear. [5]
If e1 is the fixed reference orientation in which line elements do not deform during the deformation and e1 − e2 is the plane of deformation, then the deformation gradient in simple shear can be expressed as
We can also write the deformation gradient as
In linear elasticity, shear stress, denoted , is related to shear strain, denoted , by the following equation: [6]
where is the shear modulus of the material, given by
Here is Young's modulus and is Poisson's ratio. Combining gives
In continuum mechanics, the infinitesimal strain theory is a mathematical approach to the description of the deformation of a solid body in which the displacements of the material particles are assumed to be much smaller than any relevant dimension of the body; so that its geometry and the constitutive properties of the material at each point of space can be assumed to be unchanged by the deformation.

In physics, Hooke's law is an empirical law which states that the force needed to extend or compress a spring by some distance scales linearly with respect to that distance—that is, Fs = kx, where k is a constant factor characteristic of the spring, and x is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram. He published the solution of his anagram in 1678 as: ut tensio, sic vis. Hooke states in the 1678 work that he was aware of the law since 1660.
Linear elasticity is a mathematical model of how solid objects deform and become internally stressed due to prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.
A Newtonian fluid is a fluid in which the viscous stresses arising from its flow are at every point linearly correlated to the local strain rate — the rate of change of its deformation over time. Stresses are proportional to the rate of change of the fluid's velocity vector.

Shear stress is the component of stress coplanar with a material cross section. It arises from the shear force, the component of force vector parallel to the material cross section. Normal stress, on the other hand, arises from the force vector component perpendicular to the material cross section on which it acts.
In differential geometry, the four-gradient is the four-vector analogue of the gradient from vector calculus.
In continuum mechanics, the finite strain theory—also called large strain theory, or large deformation theory—deals with deformations in which strains and/or rotations are large enough to invalidate assumptions inherent in infinitesimal strain theory. In this case, the undeformed and deformed configurations of the continuum are significantly different, requiring a clear distinction between them. This is commonly the case with elastomers, plastically-deforming materials and other fluids and biological soft tissue.
A neo-Hookean solid is a hyperelastic material model, similar to Hooke's law, that can be used for predicting the nonlinear stress-strain behavior of materials undergoing large deformations. The model was proposed by Ronald Rivlin in 1948 using invariants, though Mooney had already described a version in stretch form in 1940, and Wall had noted the equivalence in shear with the Hooke model in 1942.
In continuum mechanics, a Mooney–Rivlin solid is a hyperelastic material model where the strain energy density function is a linear combination of two invariants of the left Cauchy–Green deformation tensor . The model was proposed by Melvin Mooney in 1940 and expressed in terms of invariants by Ronald Rivlin in 1948.
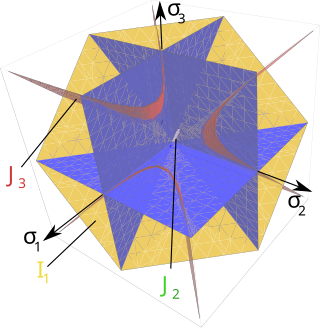
A yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the material is said to have become plastic. Further deformation of the material causes the stress state to remain on the yield surface, even though the shape and size of the surface may change as the plastic deformation evolves. This is because stress states that lie outside the yield surface are non-permissible in rate-independent plasticity, though not in some models of viscoplasticity.

In physics and continuum mechanics, deformation is the change in the shape or size of an object. It has dimension of length with SI unit of metre (m). It is quantified as the residual displacement of particles in a non-rigid body, from an initial configuration to a final configuration, excluding the body's average translation and rotation. A configuration is a set containing the positions of all particles of the body.
In mechanics, strain is defined as relative deformation, compared to a reference position configuration. Different equivalent choices may be made for the expression of a strain field depending on whether it is defined with respect to the initial or the final configuration of the body and on whether the metric tensor or its dual is considered.

In theoretical physics, the composition of two non-collinear Lorentz boosts results in a Lorentz transformation that is not a pure boost but is the composition of a boost and a rotation. This rotation is called Thomas rotation, Thomas–Wigner rotation or Wigner rotation. If a sequence of non-collinear boosts returns an object to its initial velocity, then the sequence of Wigner rotations can combine to produce a net rotation called the Thomas precession.

In continuum mechanics, plate theories are mathematical descriptions of the mechanics of flat plates that draw on the theory of beams. Plates are defined as plane structural elements with a small thickness compared to the planar dimensions. The typical thickness to width ratio of a plate structure is less than 0.1. A plate theory takes advantage of this disparity in length scale to reduce the full three-dimensional solid mechanics problem to a two-dimensional problem. The aim of plate theory is to calculate the deformation and stresses in a plate subjected to loads.
In continuum mechanics, an Arruda–Boyce model is a hyperelastic constitutive model used to describe the mechanical behavior of rubber and other polymeric substances. This model is based on the statistical mechanics of a material with a cubic representative volume element containing eight chains along the diagonal directions. The material is assumed to be incompressible. The model is named after Ellen Arruda and Mary Cunningham Boyce, who published it in 1993.
The Gent hyperelastic material model is a phenomenological model of rubber elasticity that is based on the concept of limiting chain extensibility. In this model, the strain energy density function is designed such that it has a singularity when the first invariant of the left Cauchy-Green deformation tensor reaches a limiting value .

The Kirchhoff–Love theory of plates is a two-dimensional mathematical model that is used to determine the stresses and deformations in thin plates subjected to forces and moments. This theory is an extension of Euler-Bernoulli beam theory and was developed in 1888 by Love using assumptions proposed by Kirchhoff. The theory assumes that a mid-surface plane can be used to represent a three-dimensional plate in two-dimensional form.
In mechanics and geology, pure shear is a three-dimensional homogeneous flattening of a body. It is an example of irrotational strain in which body is elongated in one direction while being shortened perpendicularly. For soft materials, such as rubber, a strain state of pure shear is often used for characterizing hyperelastic and fracture mechanical behaviour. Pure shear is differentiated from simple shear in that pure shear involves no rigid body rotation.

In continuum mechanics, the strain-rate tensor or rate-of-strain tensor is a physical quantity that describes the rate of change of the strain of a material in the neighborhood of a certain point, at a certain moment of time. It can be defined as the derivative of the strain tensor with respect to time, or as the symmetric component of the Jacobian matrix of the flow velocity. In fluid mechanics it also can be described as the velocity gradient, a measure of how the velocity of a fluid changes between different points within the fluid. Though the term can refer to a velocity profile, it is often used to mean the gradient of a flow's velocity with respect to its coordinates. The concept has implications in a variety of areas of physics and engineering, including magnetohydrodynamics, mining and water treatment.

In continuum mechanics, objective stress rates are time derivatives of stress that do not depend on the frame of reference. Many constitutive equations are designed in the form of a relation between a stress-rate and a strain-rate. The mechanical response of a material should not depend on the frame of reference. In other words, material constitutive equations should be frame-indifferent (objective). If the stress and strain measures are material quantities then objectivity is automatically satisfied. However, if the quantities are spatial, then the objectivity of the stress-rate is not guaranteed even if the strain-rate is objective.