
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. For example,

In mathematics, a simplicial complex is a structured set composed of points, line segments, triangles, and their n-dimensional counterparts, called simplices, such that all the faces and intersections of the elements are also included in the set. Simplicial complexes should not be confused with the more abstract notion of a simplicial set appearing in modern simplicial homotopy theory. The purely combinatorial counterpart to a simplicial complex is an abstract simplicial complex. To distinguish a simplicial complex from an abstract simplicial complex, the former is often called a geometric simplicial complex.
In mathematics, a building is a combinatorial and geometric structure which simultaneously generalizes certain aspects of flag manifolds, finite projective planes, and Riemannian symmetric spaces. Buildings were initially introduced by Jacques Tits as a means to understand the structure of isotropic reductive linear algebraic groups over arbitrary fields. The more specialized theory of Bruhat–Tits buildings plays a role in the study of p-adic Lie groups analogous to that of the theory of symmetric spaces in the theory of Lie groups.

In the mathematical disciplines of topology and geometry, an orbifold is a generalization of a manifold. Roughly speaking, an orbifold is a topological space that is locally a finite group quotient of a Euclidean space.
In algebraic topology, singular homology refers to the study of a certain set of algebraic invariants of a topological space , the so-called homology groups Intuitively, singular homology counts, for each dimension , the -dimensional holes of a space. Singular homology is a particular example of a homology theory, which has now grown to be a rather broad collection of theories. Of the various theories, it is perhaps one of the simpler ones to understand, being built on fairly concrete constructions.
In mathematics, the simplicial approximation theorem is a foundational result for algebraic topology, guaranteeing that continuous mappings can be approximated by ones that are piecewise of the simplest kind. It applies to mappings between spaces that are built up from simplices—that is, finite simplicial complexes. The general continuous mapping between such spaces can be represented approximately by the type of mapping that is (affine-) linear on each simplex into another simplex, at the cost (i) of sufficient barycentric subdivision of the simplices of the domain, and (ii) replacement of the actual mapping by a homotopic one.

In mathematics, the barycentric subdivision is a standard way to subdivide a given simplex into smaller ones. Its extension to simplicial complexes is a canonical method to refining them. Therefore, the barycentric subdivision is an important tool in algebraic topology.

In combinatorics, an abstract simplicial complex (ASC), often called an abstract complex or just a complex, is a family of sets that is closed under taking subsets, i.e., every subset of a set in the family is also in the family. It is a purely combinatorial description of the geometric notion of a simplicial complex. For example, in a 2-dimensional simplicial complex, the sets in the family are the triangles, their edges, and their vertices.

In mathematics, specifically algebraic topology, Čech cohomology is a cohomology theory based on the intersection properties of open covers of a topological space. It is named for the mathematician Eduard Čech.
In mathematics, a simplicial set is a sequence of sets with internal order structure and maps between them. Simplicial sets are higher-dimensional generalizations of directed graphs.
In algebraic topology, simplicial homology is the sequence of homology groups of a simplicial complex. It formalizes the idea of the number of holes of a given dimension in the complex. This generalizes the number of connected components.

In mathematics, triangulation describes the replacement of topological spaces with simplicial complexes by the choice of an appropriate homeomorphism. A space that admits such a homeomorphism is called a triangulable space. Triangulations can also be used to define a piecewise linear structure for a space, if one exists. Triangulation has various applications both in and outside of mathematics, for instance in algebraic topology, in complex analysis, and in modeling.
In mathematics, obstruction theory is a name given to two different mathematical theories, both of which yield cohomological invariants.
The link in a simplicial complex is a generalization of the neighborhood of a vertex in a graph. The link of a vertex encodes information about the local structure of the complex at the vertex.
In category theory, a discipline within mathematics, the nerveN(C) of a small category C is a simplicial set constructed from the objects and morphisms of C. The geometric realization of this simplicial set is a topological space, called the classifying space of the categoryC. These closely related objects can provide information about some familiar and useful categories using algebraic topology, most often homotopy theory.
Simplicial continuation, or piecewise linear continuation, is a one-parameter continuation method which is well suited to small to medium embedding spaces. The algorithm has been generalized to compute higher-dimensional manifolds by and.
This is a glossary of properties and concepts in algebraic topology in mathematics.
Discrete calculus or the calculus of discrete functions, is the mathematical study of incremental change, in the same way that geometry is the study of shape and algebra is the study of generalizations of arithmetic operations. The word calculus is a Latin word, meaning originally "small pebble"; as such pebbles were used for calculation, the meaning of the word has evolved and today usually means a method of computation. Meanwhile, calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the study of continuous change.
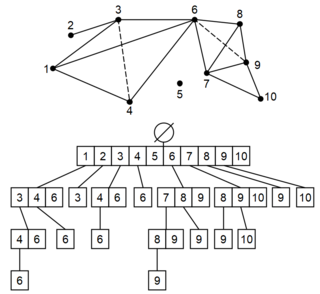
In topological data analysis, a simplex tree is a type of trie used to represent efficiently any general simplicial complex. Through its nodes, this data structure notably explicitly represents all the simplices. Its flexible structure allows the implementation of many basic operations useful to computing persistent homology. This data structure was invented by Jean-Daniel Boissonnat and Clément Maria in 2014, in the article The Simplex Tree: An Efficient Data Structure for General Simplicial Complexes. This data structure offers efficient operations on sparse simplicial complexes. For dense or maximal simplices, Skeleton-Blocker representations or Toplex Map representations are used.
A subdivision of a simplicial complex is another simplicial complex in which, intuitively, one or more simplices of the original complex have been partitioned into smaller simplices. The most commonly used subdivision is the barycentric subdivision, but the term is more general. The subdivision is defined in slightly different ways in different contexts.

































