In mathematics, a polynomial is a mathematical expression consisting of indeterminates and coefficients, that involves only the operations of addition, subtraction, multiplication and exponentiation to nonnegative integer powers, and has a finite number of terms. An example of a polynomial of a single indeterminate x is x2 − 4x + 7. An example with three indeterminates is x3 + 2xyz2 − yz + 1.
In mathematics, a quadratic equation is an equation that can be rearranged in standard form as where the variable x represents an unknown number, and a, b, and c represent known numbers, where a ≠ 0. The numbers a, b, and c are the coefficients of the equation and may be distinguished by respectively calling them, the quadratic coefficient, the linear coefficient and the constant coefficient or free term.

In elementary algebra, the quadratic formula is a closed-form expression describing the solutions of a quadratic equation. Other ways of solving quadratic equations, such as completing the square, yield the same solutions.

In mathematics, Galois theory, originally introduced by Évariste Galois, provides a connection between field theory and group theory. This connection, the fundamental theorem of Galois theory, allows reducing certain problems in field theory to group theory, which makes them simpler and easier to understand.
In mathematics, the Abel–Ruffini theorem states that there is no solution in radicals to general polynomial equations of degree five or higher with arbitrary coefficients. Here, general means that the coefficients of the equation are viewed and manipulated as indeterminates.

In mathematics, a root of unity, occasionally called a de Moivre number, is any complex number that yields 1 when raised to some positive integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, and the discrete Fourier transform.

In algebra, a cubic equation in one variable is an equation of the form in which a is not zero.

In mathematics, a quartic equation is one which can be expressed as a quartic function equaling zero. The general form of a quartic equation is

In mathematics, a quintic function is a function of the form

In algebra, a quartic function is a function of the form
In mathematics, an algebraic equation or polynomial equation is an equation of the form , where P is a polynomial with coefficients in some field, often the field of the rational numbers. For example, is an algebraic equation with integer coefficients and
In algebra, the theory of equations is the study of algebraic equations, which are equations defined by a polynomial. The main problem of the theory of equations was to know when an algebraic equation has an algebraic solution. This problem was completely solved in 1830 by Évariste Galois, by introducing what is now called Galois theory.
In mathematics, an expression or equation is in closed form if it is formed with constants, variables and a finite set of basic functions connected by arithmetic operations and function composition. Commonly, the allowed functions are nth root, exponential function, logarithm, and trigonometric functions. However, the set of basic functions depends on the context.
In mathematics, an algebraic function is a function that can be defined as the root of an irreducible polynomial equation. Algebraic functions are often algebraic expressions using a finite number of terms, involving only the algebraic operations addition, subtraction, multiplication, division, and raising to a fractional power. Examples of such functions are:

In algebra, the Bring radical or ultraradical of a real number a is the unique real root of the polynomial
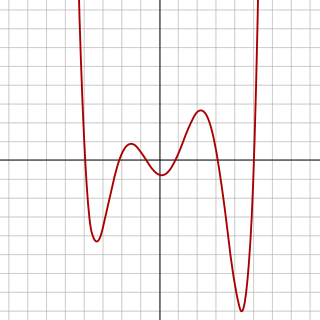
In algebra, a sexticpolynomial is a polynomial of degree six. A sextic equation is a polynomial equation of degree six—that is, an equation whose left hand side is a sextic polynomial and whose right hand side is zero. More precisely, it has the form:
In algebra, casus irreducibilis is one of the cases that may arise in solving polynomials of degree 3 or higher with integer coefficients algebraically, i.e., by obtaining roots that are expressed with radicals. It shows that many algebraic numbers are real-valued but cannot be expressed in radicals without introducing complex numbers. The most notable occurrence of casus irreducibilis is in the case of cubic polynomials that have three real roots, which was proven by Pierre Wantzel in 1843. One can see whether a given cubic polynomial is in the so-called casus irreducibilis by looking at the discriminant, via Cardano's formula.
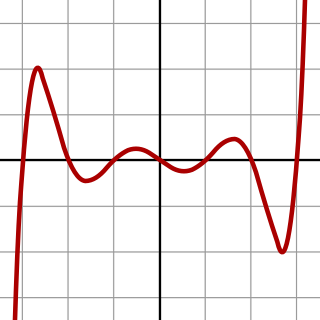
In algebra, a septic equation is an equation of the form
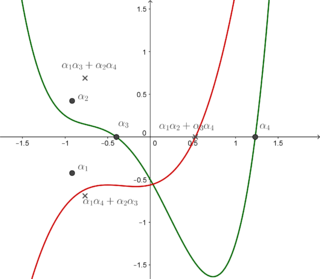
In algebra, a resolvent cubic is one of several distinct, although related, cubic polynomials defined from a monic polynomial of degree four:
In Galois theory, a discipline within the field of abstract algebra, a resolvent for a permutation group G is a polynomial whose coefficients depend polynomially on the coefficients of a given polynomial p and has, roughly speaking, a rational root if and only if the Galois group of p is included in G. More exactly, if the Galois group is included in G, then the resolvent has a rational root, and the converse is true if the rational root is a simple root. Resolvents were introduced by Joseph Louis Lagrange and systematically used by Évariste Galois. Nowadays they are still a fundamental tool to compute Galois groups. The simplest examples of resolvents are
















