In mathematics, a finite field or Galois field is a field that contains a finite number of elements. As with any field, a finite field is a set on which the operations of multiplication, addition, subtraction and division are defined and satisfy certain basic rules. The most common examples of finite fields are given by the integers mod p when p is a prime number.
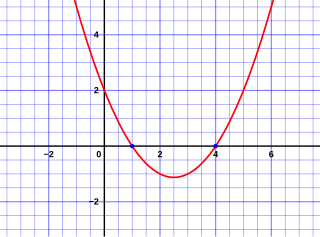
In elementary algebra, the quadratic formula is a formula that provides the two solutions, or roots, to a quadratic equation. There are other ways of solving a quadratic equation instead of using the quadratic formula, such as completing the square.

In mathematics, Galois theory, originally introduced by Évariste Galois, provides a connection between field theory and group theory. This connection, the fundamental theorem of Galois theory, allows reducing certain problems in field theory to group theory, which makes them simpler and easier to understand.

In mathematics, more specifically in the field of group theory, a solvable group or soluble group is a group that can be constructed from abelian groups using extensions. Equivalently, a solvable group is a group whose derived series terminates in the trivial subgroup.
In mathematics, the Abel–Ruffini theorem states that there is no solution in radicals to general polynomial equations of degree five or higher with arbitrary coefficients. Here, general means that the coefficients of the equation are viewed and manipulated as indeterminates.

In mathematics, a quintic function is a function of the form
In mathematics, a linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form
In mathematics, an algebraic equation or polynomial equation is an equation of the form , where P is a polynomial with coefficients in some field, often the field of the rational numbers. For example, is an algebraic equation with integer coefficients and
In mathematics and its applications, a Sturm–Liouville problem is a second-order linear ordinary differential equation of the form:

In mathematics, a Tschirnhaus transformation, also known as Tschirnhausen transformation, is a type of mapping on polynomials developed by Ehrenfried Walther von Tschirnhaus in 1683.
In Galois theory, the inverse Galois problem concerns whether or not every finite group appears as the Galois group of some Galois extension of the rational numbers . This problem, first posed in the early 19th century, is unsolved.
In abstract algebra, Hilbert's Theorem 90 (or Satz 90) is an important result on cyclic extensions of fields (or to one of its generalizations) that leads to Kummer theory. In its most basic form, it states that if L/K is an extension of fields with cyclic Galois group G = Gal(L/K) generated by an element and if is an element of L of relative norm 1, that is
A solution in radicals or algebraic solution is a closed-form expression, and more specifically a closed-form algebraic expression, that is the solution of a polynomial equation, and relies only on addition, subtraction, multiplication, division, raising to integer powers, and the extraction of nth roots.

In algebra, the Bring radical or ultraradical of a real number a is the unique real root of the polynomial
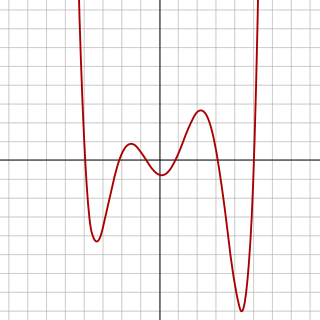
In algebra, a sexticpolynomial is a polynomial of degree six. A sextic equation is a polynomial equation of degree six—that is, an equation whose left hand side is a sextic polynomial and whose right hand side is zero. More precisely, it has the form:
In algebra, casus irreducibilis is one of the cases that may arise in solving polynomials of degree 3 or higher with integer coefficients algebraically, i.e., by obtaining roots that are expressed with radicals. It shows that many algebraic numbers are real-valued but cannot be expressed in radicals without introducing complex numbers. The most notable occurrence of casus irreducibilis is in the case of cubic polynomials that have three real roots, which was proven by Pierre Wantzel in 1843. One can see whether a given cubic polynomial is in so-called casus irreducibilis by looking at the discriminant, via Cardano's formula.
In mathematics and more specifically in field theory, a radical extension of a field K is an extension of K that is obtained by adjoining a sequence of nth roots of elements.
In mathematics, Thomae's formula is a formula introduced by Carl Johannes Thomae (1870) relating theta constants to the branch points of a hyperelliptic curve.
In mathematics, a superelliptic curve is an algebraic curve defined by an equation of the form
In mathematics, an Artin–Schreier curve is a plane curve defined over an algebraically closed field of characteristic by an equation















