| Sousselier graph | |
|---|---|
 | |
| Vertices | 16 |
| Edges | 27 |
| Radius | 2 |
| Diameter | 3 |
| Girth | 5 |
| Automorphisms | 2 |
| Chromatic number | 3 |
| Chromatic index | 5 |
| Book thickness | 3 |
| Queue number | 2 |
| Table of graphs and parameters | |
The Sousselier graph is, in graph theory, a hypohamiltonian graph with 16 vertices and 27 edges. It has book thickness 3 and queue number 2. [1]
Hypohamiltonian graphs were first studied by Sousselier in Problèmes plaisants et délectables (1963) . [2]
In 1967, Lindgren builds an infinite sequence of hypohamiltonian graphs. The graphs of this sequence all have 6k+10 vertices, for every integer k. [3] The same sequence of hypohamiltonian graphs is independently built by Sousselier. [4] In 1973 Chvátal explains in a scientific paper how edges can be added to some hypohamiltonian graphs in order to build new ones of the same order, and he names Bondy [5] as the original author of the method. As an illustration, he shows that two edges can be added to the second graph of the Lindgren sequence (which he names Sousselier sequence) in order to build a new hypohamiltonian graph on 16 vertices. This graph is named the Sousselier graph.
Kőnig's lemma or Kőnig's infinity lemma is a theorem in graph theory due to the Hungarian mathematician Dénes Kőnig who published it in 1927. It gives a sufficient condition for an infinite graph to have an infinitely long path. The computability aspects of this theorem have been thoroughly investigated by researchers in mathematical logic, especially in computability theory. This theorem also has important roles in constructive mathematics and proof theory.
In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles. That is, it consists of vertices and edges, with each edge directed from one vertex to another, such that following those directions will never form a closed loop. A directed graph is a DAG if and only if it can be topologically ordered, by arranging the vertices as a linear ordering that is consistent with all edge directions. DAGs have numerous scientific and computational applications, ranging from biology to information science to computation (scheduling).
In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected or directed graph that visits each vertex exactly once. A Hamiltonian cycle is a cycle that visits each vertex exactly once. A Hamiltonian path that starts and ends at adjacent vertices can be completed by adding one more edge to form a Hamiltonian cycle, and removing any edge from a Hamiltonian cycle produces a Hamiltonian path. Determining whether such paths and cycles exist in graphs are NP-complete.
In graph theory, a component of an undirected graph is a connected subgraph that is not part of any larger connected subgraph. The components of any graph partition its vertices into disjoint sets, and are the induced subgraphs of those sets. A graph that is itself connected has exactly one component, consisting of the whole graph. Components are sometimes called connected components.
Informally, the reconstruction conjecture in graph theory says that graphs are determined uniquely by their subgraphs. It is due to Kelly and Ulam.
In the mathematical field of graph theory, a spanning treeT of an undirected graph G is a subgraph that is a tree which includes all of the vertices of G. In general, a graph may have several spanning trees, but a graph that is not connected will not contain a spanning tree. If all of the edges of G are also edges of a spanning tree T of G, then G is a tree and is identical to T.
In the mathematical field of graph theory, a snark is an undirected graph with exactly three edges per vertex whose edges cannot be colored with only three colors. In order to avoid trivial cases, snarks are often restricted to have additional requirements on their connectivity and on the length of their cycles. Infinitely many snarks exist.
In the mathematical field of graph theory, a quartic graph is a graph where all vertices have degree 4. In other words, a quartic graph is a 4-regular graph.
In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally independent graphs.
In the mathematical field of graph theory, the Grötzsch graph is a triangle-free graph with 11 vertices, 20 edges, chromatic number 4, and crossing number 5. It is named after German mathematician Herbert Grötzsch, who used it as an example in connection with his 1959 theorem that planar triangle-free graphs are 3-colorable.
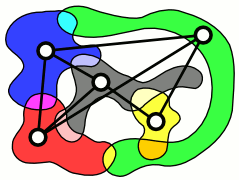
In graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph can be represented as an intersection graph, but some important special classes of graphs can be defined by the types of sets that are used to form an intersection representation of them.
In the mathematical field of graph theory, the Rado graph, Erdős–Rényi graph, or random graph is a countably infinite graph that can be constructed by choosing independently at random for each pair of its vertices whether to connect the vertices by an edge. The names of this graph honor Richard Rado, Paul Erdős, and Alfréd Rényi, mathematicians who studied it in the early 1960s; it appears even earlier in the work of Wilhelm Ackermann (1937). The Rado graph can also be constructed non-randomly, by symmetrizing the membership relation of the hereditarily finite sets, by applying the BIT predicate to the binary representations of the natural numbers, or as an infinite Paley graph that has edges connecting pairs of prime numbers congruent to 1 mod 4 that are quadratic residues modulo each other.
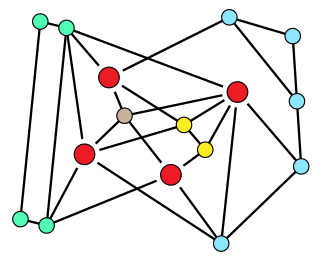
In graph theory, toughness is a measure of the connectivity of a graph. A graph G is said to be t-tough for a given real number t if, for every integer k > 1, G cannot be split into k different connected components by the removal of fewer than tk vertices. For instance, a graph is 1-tough if the number of components formed by removing a set of vertices is always at most as large as the number of removed vertices. The toughness of a graph is the maximum t for which it is t-tough; this is a finite number for all finite graphs except the complete graphs, which by convention have infinite toughness.
Václav (Vašek) Chvátal is a Professor Emeritus in the Department of Computer Science and Software Engineering at Concordia University in Montreal, Quebec, Canada and a Visiting Professor at Charles University in Prague. He has published extensively on topics in graph theory, combinatorics, and combinatorial optimization.
In the mathematical field of graph theory, a graph G is said to be hypohamiltonian if G itself does not have a Hamiltonian cycle but every graph formed by removing a single vertex from G is Hamiltonian.
In graph theory, a perfectly orderable graph is a graph whose vertices can be ordered in such a way that a greedy coloring algorithm with that ordering optimally colors every induced subgraph of the given graph. Perfectly orderable graphs form a special case of the perfect graphs, and they include the chordal graphs, comparability graphs, and distance-hereditary graphs. However, testing whether a graph is perfectly orderable is NP-complete.
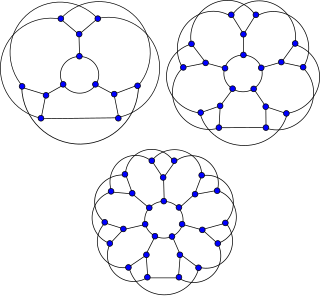
In the mathematical field of graph theory, the flower snarks form an infinite family of snarks introduced by Rufus Isaacs in 1975.
In the mathematical field of graph theory, the friendship graphFn is a planar, undirected graph with 2n + 1 vertices and 3n edges.
In graph theory, a branch of mathematics, Fleischner's theorem gives a sufficient condition for a graph to contain a Hamiltonian cycle. It states that, if G is a 2-vertex-connected graph, then the square of G is Hamiltonian. it is named after Herbert Fleischner, who published its proof in 1974.
The Wiener–Araya graph is, in graph theory, a graph on 42 vertices with 67 edges. It is hypohamiltonian, which means that it does not itself have a Hamiltonian cycle but every graph formed by removing a single vertex from it is Hamiltonian. It is also planar.