Proof of Miquel's quadrilateral theorem
Spiral similarity can be used to prove Miquel's quadrilateral theorem: given four noncollinear points  and
and  , the circumcircles of the four triangles
, the circumcircles of the four triangles  and
and  intersect at one point, where
intersect at one point, where  is the intersection of
is the intersection of  and
and  and
and  is the intersection of
is the intersection of  and
and  (see diagram). [1]
(see diagram). [1]
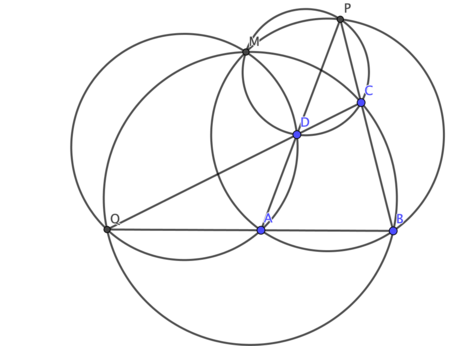
Let  be the center of the spiral similarity which takes
be the center of the spiral similarity which takes  to
to  . By the above construction, the circumcircles of
. By the above construction, the circumcircles of  and
and  intersect at
intersect at  and
and  . Since
. Since  is also the center of the spiral similarity taking
is also the center of the spiral similarity taking  to
to  , by similar reasoning the circumcircles of
, by similar reasoning the circumcircles of  and
and  meet at
meet at  and
and  . Thus, all four circles intersect at
. Thus, all four circles intersect at  . [1]
. [1]
Example problem
Here is an example problem on the 2018 Japan MO Finals which can be solved using spiral similarity:
Given a scalene triangle  , let
, let  and
and  be points on segments
be points on segments  and
and  , respectively, so that
, respectively, so that  . Let
. Let  be the circumcircle of triangle
be the circumcircle of triangle  and
and  the reflection of
the reflection of  across
across  . Lines
. Lines  and
and  meet
meet  again at
again at  and
and  , respectively. Prove that
, respectively. Prove that  and
and  intersect on
intersect on  . [5]
. [5]

Proof: We first prove the following claims:
Claim 1: Quadrilateral  is cyclic.
is cyclic.
Proof: Since  is isosceles, we note that
is isosceles, we note that  thus proving that quadrilateral
thus proving that quadrilateral  is cyclic, as desired. By symmetry, we can prove that quadrilateral
is cyclic, as desired. By symmetry, we can prove that quadrilateral  is cyclic.
is cyclic.
Claim 2: 
Proof: We have that  By similar reasoning,
By similar reasoning,  so by AA similarity,
so by AA similarity,  as desired.
as desired.
We now note that  is the spiral center that maps
is the spiral center that maps  to
to  . Let
. Let  be the intersection of
be the intersection of  and
and  . By the spiral similarity construction above, the spiral center must be the intersection of the circumcircles of
. By the spiral similarity construction above, the spiral center must be the intersection of the circumcircles of  and
and  . However, this point is
. However, this point is  , so thus points
, so thus points  must be concyclic. Hence,
must be concyclic. Hence,  must lie on
must lie on  , as desired.
, as desired.
































































































