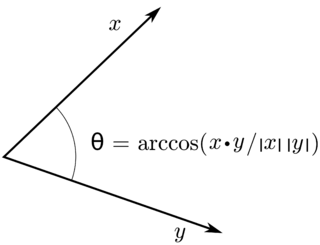
In mathematics, an inner product space is a real vector space or a complex vector space with an operation called an inner product. The inner product of two vectors in the space is a scalar, often denoted with angle brackets such as in . Inner products allow formal definitions of intuitive geometric notions, such as lengths, angles, and orthogonality of vectors. Inner product spaces generalize Euclidean vector spaces, in which the inner product is the dot product or scalar product of Cartesian coordinates. Inner product spaces of infinite dimension are widely used in functional analysis. Inner product spaces over the field of complex numbers are sometimes referred to as unitary spaces. The first usage of the concept of a vector space with an inner product is due to Giuseppe Peano, in 1898.
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The direct sum of modules is the smallest module which contains the given modules as submodules with no "unnecessary" constraints, making it an example of a coproduct. Contrast with the direct product, which is the dual notion.
In mathematics, a formal series is an infinite sum that is considered independently from any notion of convergence, and can be manipulated with the usual algebraic operations on series.
In mathematics, specifically ring theory, a principal ideal is an ideal in a ring that is generated by a single element of through multiplication by every element of The term also has another, similar meaning in order theory, where it refers to an (order) ideal in a poset generated by a single element which is to say the set of all elements less than or equal to in
In mathematics, specifically functional analysis, a trace-class operator is a linear operator for which a trace may be defined, such that the trace is a finite number independent of the choice of basis used to compute the trace. This trace of trace-class operators generalizes the trace of matrices studied in linear algebra. All trace-class operators are compact operators.
In linear algebra and functional analysis, the partial trace is a generalization of the trace. Whereas the trace is a scalar valued function on operators, the partial trace is an operator-valued function. The partial trace has applications in quantum information and decoherence which is relevant for quantum measurement and thereby to the decoherent approaches to interpretations of quantum mechanics, including consistent histories and the relative state interpretation.
Kripke semantics is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke and André Joyal. It was first conceived for modal logics, and later adapted to intuitionistic logic and other non-classical systems. The development of Kripke semantics was a breakthrough in the theory of non-classical logics, because the model theory of such logics was almost non-existent before Kripke.
In linear algebra, the Gram matrix of a set of vectors in an inner product space is the Hermitian matrix of inner products, whose entries are given by the inner product . If the vectors are the columns of matrix then the Gram matrix is in the general case that the vector coordinates are complex numbers, which simplifies to for the case that the vector coordinates are real numbers.
In mathematics, weak convergence in a Hilbert space is convergence of a sequence of points in the weak topology.
In descriptive set theory, a tree on a set is a collection of finite sequences of elements of such that every prefix of a sequence in the collection also belongs to the collection.
In mathematics, and in particular functional analysis, the tensor product of Hilbert spaces is a way to extend the tensor product construction so that the result of taking a tensor product of two Hilbert spaces is another Hilbert space. Roughly speaking, the tensor product is the metric space completion of the ordinary tensor product. This is an example of a topological tensor product. The tensor product allows Hilbert spaces to be collected into a symmetric monoidal category.
In mathematics, the Fréchet derivative is a derivative defined on normed spaces. Named after Maurice Fréchet, it is commonly used to generalize the derivative of a real-valued function of a single real variable to the case of a vector-valued function of multiple real variables, and to define the functional derivative used widely in the calculus of variations.
Axiomatic constructive set theory is an approach to mathematical constructivism following the program of axiomatic set theory. The same first-order language with "" and "" of classical set theory is usually used, so this is not to be confused with a constructive types approach. On the other hand, some constructive theories are indeed motivated by their interpretability in type theories.
In the mathematical discipline of functional analysis, the concept of a compact operator on Hilbert space is an extension of the concept of a matrix acting on a finite-dimensional vector space; in Hilbert space, compact operators are precisely the closure of finite-rank operators in the topology induced by the operator norm. As such, results from matrix theory can sometimes be extended to compact operators using similar arguments. By contrast, the study of general operators on infinite-dimensional spaces often requires a genuinely different approach.
In logic, a modal companion of a superintuitionistic (intermediate) logic L is a normal modal logic that interprets L by a certain canonical translation, described below. Modal companions share various properties of the original intermediate logic, which enables to study intermediate logics using tools developed for modal logic.
In logic, general frames are Kripke frames with an additional structure, which are used to model modal and intermediate logics. The general frame semantics combines the main virtues of Kripke semantics and algebraic semantics: it shares the transparent geometrical insight of the former, and robust completeness of the latter.
In intuitionistic mathematics, a choice sequence is a constructive formulation of a sequence. Since the Intuitionistic school of mathematics, as formulated by L. E. J. Brouwer, rejects the idea of a completed infinity, in order to use a sequence, we must have a formulation of a finite, constructible object that can serve the same purpose as a sequence. Thus, Brouwer formulated the choice sequence, which is given as a construction, rather than an abstract, infinite object.

In mathematics, Hilbert spaces allow generalizing the methods of linear algebra and calculus from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. Hilbert spaces arise naturally and frequently in mathematics and physics, typically as function spaces. Formally, a Hilbert space is a vector space equipped with an inner product that defines a distance function for which the space is a complete metric space.
Coherent states have been introduced in a physical context, first as quasi-classical states in quantum mechanics, then as the backbone of quantum optics and they are described in that spirit in the article Coherent states. However, they have generated a huge variety of generalizations, which have led to a tremendous amount of literature in mathematical physics. In this article, we sketch the main directions of research on this line. For further details, we refer to several existing surveys.
The finite promise games are a collection of mathematical games developed by American mathematician Harvey Friedman in 2009 which are used to develop a family of fast-growing functions , and . The greedy clique sequence is a graph theory concept, also developed by Friedman in 2010, which are used to develop fast-growing functions , and .





















