Stability postulate

Last updated February 04, 2023

In probability theory, to obtain a nondegenerate limiting distribution of the extreme value distribution, it is necessary to "reduce" the actual greatest value by applying a linear transformation with coefficients that depend on the sample size.

If $X_{1},X_{2},\dots ,X_{n}$ are independent random variables with common probability density function

p_{X_{j}}(x)=f(x),

then the cumulative distribution function of $X'_{n}=\max\{\,X_{1},\ldots ,X_{n}\,\}$ is

F_{X'_{n}}={[F(x)]}^{n}

If there is a limiting distribution of interest, the stability postulate states the limiting distribution is some sequence of transformed "reduced" values, such as $(a_{n}X'_{n}+b_{n})$ , where $a_{n},b_{n}$ may depend on n but not on x.

To distinguish the limiting cumulative distribution function from the "reduced" greatest value from F(x), we will denote it by G(x). It follows that G(x) must satisfy the functional equation

{[G(x)]}^{n}=G{(a_{n}x+b_{n})}

This equation was obtained by Maurice René Fréchet and also by Ronald Fisher.

Boris Vladimirovich Gnedenko has shown there are no other distributions satisfying the stability postulate other than the following^[1]:

Gumbel distribution for the minimum stability postulate
- If $X_{i}={\textrm {Gumbel}}(\mu ,\beta )$ and $Y=\min\{\,X_{1},\ldots ,X_{n}\,\}$ then $Y\sim a_{n}X+b_{n}$ where $a_{n}=1$ and $b_{n}=\beta \log(n)$
- In other words, $Y\sim {\textrm {Gumbel}}(\mu -\beta \log(n),\beta )$
Extreme value distribution for the maximum stability postulate
- If $X_{i}={\textrm {EV}}(\mu ,\sigma )$ and $Y=\max\{\,X_{1},\ldots ,X_{n}\,\}$ then $Y\sim a_{n}X+b_{n}$ where $a_{n}=1$ and $b_{n}=\sigma \log({\tfrac {1}{n}})$
- In other words, $Y\sim {\textrm {EV}}(\mu -\sigma \log({\tfrac {1}{n}}),\sigma )$
Fréchet distribution for the maximum stability postulate
- If $X_{i}={\textrm {Frechet}}(\alpha ,s,m)$ and $Y=\max\{\,X_{1},\ldots ,X_{n}\,\}$ then $Y\sim a_{n}X+b_{n}$ where $a_{n}=n^{-{\tfrac {1}{\alpha }}}$ and $b_{n}=m\left(1-n^{-{\tfrac {1}{\alpha }}}\right)$
- In other words, $Y\sim {\textrm {Frechet}}(\alpha ,n^{\tfrac {1}{\alpha }}s,m)$

Related Research Articles

The Pareto distribution, named after the Italian civil engineer, economist, and sociologist Vilfredo Pareto, is a power-law probability distribution that is used in description of social, quality control, scientific, geophysical, actuarial, and many other types of observable phenomena; the principle originally applied to describing the distribution of wealth in a society, fitting the trend that a large portion of wealth is held by a small fraction of the population. The Pareto principle or "80-20 rule" stating that 80% of outcomes are due to 20% of causes was named in honour of Pareto, but the concepts are distinct, and only Pareto distributions with shape value of log₄5 ≈ 1.16 precisely reflect it. Empirical observation has shown that this 80-20 distribution fits a wide range of cases, including natural phenomena and human activities.

<span class="mw-page-title-main">Gumbel distribution</span> Particular case of the generalized extreme value distribution

In probability theory and statistics, the Gumbel distribution is used to model the distribution of the maximum of a number of samples of various distributions.

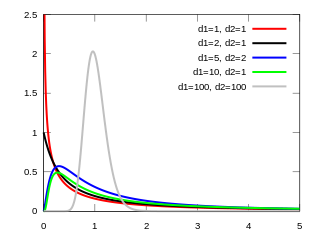
In probability theory and statistics, the F-distribution or F-ratio, also known as Snedecor's F distribution or the Fisher–Snedecor distribution is a continuous probability distribution that arises frequently as the null distribution of a test statistic, most notably in the analysis of variance (ANOVA) and other F-tests.

<span class="mw-page-title-main">Logistic distribution</span> Continuous probability distribution

In probability theory and statistics, the logistic distribution is a continuous probability distribution. Its cumulative distribution function is the logistic function, which appears in logistic regression and feedforward neural networks. It resembles the normal distribution in shape but has heavier tails. The logistic distribution is a special case of the Tukey lambda distribution.

In probability theory and statistics, the Laplace distribution is a continuous probability distribution named after Pierre-Simon Laplace. It is also sometimes called the double exponential distribution, because it can be thought of as two exponential distributions spliced together along the abscissa, although the term is also sometimes used to refer to the Gumbel distribution. The difference between two independent identically distributed exponential random variables is governed by a Laplace distribution, as is a Brownian motion evaluated at an exponentially distributed random time. Increments of Laplace motion or a variance gamma process evaluated over the time scale also have a Laplace distribution.

In probability theory, the Landau distribution is a probability distribution named after Lev Landau. Because of the distribution's "fat" tail, the moments of the distribution, like mean or variance, are undefined. The distribution is a particular case of stable distribution.

In probability theory and statistics, the Lévy distribution, named after Paul Lévy, is a continuous probability distribution for a non-negative random variable. In spectroscopy, this distribution, with frequency as the dependent variable, is known as a van der Waals profile. It is a special case of the inverse-gamma distribution. It is a stable distribution.

In probability theory and statistics, the generalized extreme value (GEV) distribution is a family of continuous probability distributions developed within extreme value theory to combine the Gumbel, Fréchet and Weibull families also known as type I, II and III extreme value distributions. By the extreme value theorem the GEV distribution is the only possible limit distribution of properly normalized maxima of a sequence of independent and identically distributed random variables. Note that a limit distribution needs to exist, which requires regularity conditions on the tail of the distribution. Despite this, the GEV distribution is often used as an approximation to model the maxima of long (finite) sequences of random variables.

In probability theory and statistics, the inverse gamma distribution is a two-parameter family of continuous probability distributions on the positive real line, which is the distribution of the reciprocal of a variable distributed according to the gamma distribution.

In probability and statistics, the Kumaraswamy's double bounded distribution is a family of continuous probability distributions defined on the interval (0,1). It is similar to the Beta distribution, but much simpler to use especially in simulation studies since its probability density function, cumulative distribution function and quantile functions can be expressed in closed form. This distribution was originally proposed by Poondi Kumaraswamy for variables that are lower and upper bounded with a zero-inflation. This was extended to inflations at both extremes [0,1] in later work with S. G. Fletcher.

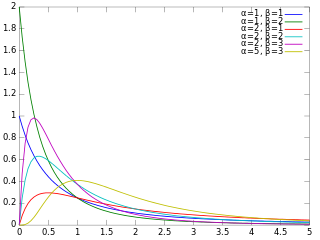
In probability theory and statistics, the beta prime distribution is an absolutely continuous probability distribution.

A ratio distribution is a probability distribution constructed as the distribution of the ratio of random variables having two other known distributions. Given two random variables X and Y, the distribution of the random variable Z that is formed as the ratio Z = X/Y is a ratio distribution.

The Fréchet distribution, also known as inverse Weibull distribution, is a special case of the generalized extreme value distribution. It has the cumulative distribution function

<span class="mw-page-title-main">Log-logistic distribution</span>

In probability and statistics, the log-logistic distribution is a continuous probability distribution for a non-negative random variable. It is used in survival analysis as a parametric model for events whose rate increases initially and decreases later, as, for example, mortality rate from cancer following diagnosis or treatment. It has also been used in hydrology to model stream flow and precipitation, in economics as a simple model of the distribution of wealth or income, and in networking to model the transmission times of data considering both the network and the software.

<span class="mw-page-title-main">Shifted log-logistic distribution</span>

The shifted log-logistic distribution is a probability distribution also known as the generalized log-logistic or the three-parameter log-logistic distribution. It has also been called the generalized logistic distribution, but this conflicts with other uses of the term: see generalized logistic distribution.

<span class="mw-page-title-main">Normal-inverse-gamma distribution</span>

In probability theory and statistics, the normal-inverse-gamma distribution is a four-parameter family of multivariate continuous probability distributions. It is the conjugate prior of a normal distribution with unknown mean and variance.

In mathematics, the Fréchet distance is a measure of similarity between curves that takes into account the location and ordering of the points along the curves. It is named after Maurice Fréchet.

Least-squares support-vector machines (LS-SVM) for statistics and in statistical modeling, are least-squares versions of support-vector machines (SVM), which are a set of related supervised learning methods that analyze data and recognize patterns, and which are used for classification and regression analysis. In this version one finds the solution by solving a set of linear equations instead of a convex quadratic programming (QP) problem for classical SVMs. Least-squares SVM classifiers were proposed by Johan Suykens and Joos Vandewalle. LS-SVMs are a class of kernel-based learning methods.

In probability, statistics, economics, and actuarial science, the Benini distribution is a continuous probability distribution that is a statistical size distribution often applied to model incomes, severity of claims or losses in actuarial applications, and other economic data. Its tail behavior decays faster than a power law, but not as fast as an exponential. This distribution was introduced by Rodolfo Benini in 1905. Somewhat later than Benini's original work, the distribution has been independently discovered or discussed by a number of authors.

In probability theory and statistics, the discrete Weibull distribution is the discrete variant of the Weibull distribution. It was first described by Nakagawa and Osaki in 1975.

References

↑ Gnedenko, B. (1943). "Sur La Distribution Limite Du Terme Maximum D'Une Serie Aleatoire". Annals of Mathematics. 44 (3): 423–453. doi:10.2307/1968974.

This statistics-related article is a stub. You can help Wikipedia by expanding it.

This probability-related article is a stub. You can help Wikipedia by expanding it.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Gnedenko, B. (1943). "Sur La Distribution Limite Du Terme Maximum D'Une Serie Aleatoire". Annals of Mathematics. 44 (3): 423–453. doi:10.2307/1968974.

[1]