Stacked polytope

Last updated

In polyhedral combinatorics (a branch of mathematics), a stacked polytope is a polytope formed from a simplex by repeatedly gluing another simplex onto one of its facets. [1]

Polyhedral combinatorics is a branch of mathematics, within combinatorics and discrete geometry, that studies the problems of counting and describing the faces of convex polyhedra and higher-dimensional convex polytopes.

In elementary geometry, a polytope is a geometric object with "flat" sides. It is a generalization in any number of dimensions of the three-dimensional polyhedron. Polytopes may exist in any general number of dimensions n as an n-dimensional polytope or n-polytope. Flat sides mean that the sides of a (k+1)-polytope consist of k-polytopes that may have (k-1)-polytopes in common. For example, a two-dimensional polygon is a 2-polytope and a three-dimensional polyhedron is a 3-polytope.

Simplex generalization of the notion of a triangle or tetrahedron to arbitrary dimensions

In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. Specifically, a k-simplex is a k-dimensional polytope which is the convex hull of its k + 1 vertices. More formally, suppose the k + 1 points are affinely independent, which means are linearly independent. Then, the simplex determined by them is the set of points

Contents

Examples

Every simplex is itself a stacked polytope.

In three dimensions, every stacked polytope is a polyhedron with triangular faces, and several of the deltahedra (polyhedra with equilateral triangle faces) are stacked polytopes

Polyhedron solid in three dimensions with flat faces

In geometry, a polyhedron is a solid in three dimensions with flat polygonal faces, straight edges and sharp corners or vertices. The word polyhedron comes from the Classical Greek πολύεδρον, as poly- + -hedron.

Deltahedron polyhedron whose faces are all equilateral triangles

In geometry, a deltahedron is a polyhedron whose faces are all equilateral triangles. The name is taken from the Greek majuscule delta (Δ), which has the shape of an equilateral triangle. There are infinitely many deltahedra, but of these only eight are convex, having 4, 6, 8, 10, 12, 14, 16 and 20 faces. The number of faces, edges, and vertices is listed below for each of the eight convex deltahedra.

Equilateral triangle triangle with three equal sides

In geometry, an equilateral triangle is a triangle in which all three sides are equal. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle.

Quadaugmented tetrahedron.png
Pentagonal dipyramid.png
The quadaugmented tetrahedron on the left is a stacked polytope, but the pentagonal bipyramid on the right is not

In a stacked polytope, each newly added simplex is only allowed to touch one of the facets of the previous ones. Thus, for instance, the quadaugmented tetrahedron, a shape formed by gluing together five regular tetrahedra around a common line segment is a stacked polytope (it has a small gap between the first and last tetrahedron). However, the similar-looking pentagonal bipyramid is not a stacked polytope, because if it is formed by gluing tetrahedra together, the last tetrahedron will be glued to two triangular faces of previous tetrahedra instead of only one.

Pentagonal bipyramid third of the infinite set of face-transitive bipyramids

In geometry, the pentagonal bipyramid is third of the infinite set of face-transitive bipyramids. Each bipyramid is the dual of a uniform prism.

Other non-convex stacked deltahedra include:

Biaugmented tetrahedron.png Triaugmented tetrahedron.png 5-cell net.png
Three tetrahedraFour tetrahedraFive tetrahedra

Combinatorial structure

An Apollonian network, the graph of a stacked polyhedron Apollonian-network.svg
An Apollonian network, the graph of a stacked polyhedron

The undirected graph formed by the vertices and edges of a stacked polytope in d dimensions is a (d + 1)-tree. More precisely, the graphs of stacked polytopes are exactly the (d + 1)-trees in which every d-vertex clique (complete subgraph) is contained in at most two (d + 1)-vertex cliques. [2] For instance, the graphs of three-dimensional stacked polyhedra are exactly the Apollonian networks, the graphs formed from a triangle by repeatedly subdividing a triangular face of the graph into three smaller triangles.

K-tree

In graph theory, a k-tree is an undirected graph formed by starting with a (k + 1)-vertex complete graph and then repeatedly adding vertices in such a way that each added vertex v has exactly k neighbors U such that, together, the k + 1 vertices formed by v and U form a clique.

Clique (graph theory) subset of the vertices of a node-link graph that are all adjacent to each other

In the mathematical area of graph theory, a clique is a subset of vertices of an undirected graph such that every two distinct vertices in the clique are adjacent; that is, its induced subgraph is complete. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs. Cliques have also been studied in computer science: the task of finding whether there is a clique of a given size in a graph is NP-complete, but despite this hardness result, many algorithms for finding cliques have been studied.

Apollonian network

In combinatorial mathematics, an Apollonian network is an undirected graph formed by a process of recursively subdividing a triangle into three smaller triangles. Apollonian networks may equivalently be defined as the planar 3-trees, the maximal planar chordal graphs, the uniquely 4-colorable planar graphs, and the graphs of stacked polytopes. They are named after Apollonius of Perga, who studied a related circle-packing construction.

One reason for the significance of stacked polytopes is that, among all d-dimensional simplicial polytopes with a given number of vertices, the stacked polytopes have the fewest possible higher-dimensional faces. For three-dimensional simplicial polyhedra the numbers of edges and two-dimensional faces are determined from the number of vertices by Euler's formula, regardless of whether the polyhedron is stacked, but this is not true in higher dimensions. Analogously, the simplicial polytopes that maximize the number of higher-dimensional faces for their number of vertices are the cyclic polytopes. [1]

In geometry, a simplicial polytope is a polytope whose facets are all simplices.

In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent. It is commonly denoted by .

In mathematics, a cyclic polytope, denoted C(n,d), is a convex polytope formed as a convex hull of n distinct points on a rational normal curve in Rd, where n is greater than d. These polytopes were studied by Constantin Carathéodory, David Gale, Theodore Motzkin, Victor Klee, and others. They play an important role in polyhedral combinatorics: according to the upper bound theorem, proved by Peter McMullen and Richard Stanley, the boundary Δ(n,d) of the cyclic polytope C(n,d) maximizes the number fi of i-dimensional faces among all simplicial spheres of dimension d − 1 with n vertices.

Related Research Articles

Cuboctahedron Archimedean solid

In geometry, a cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive.

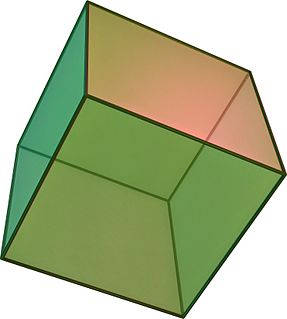
Cube A geometric shape with 6 square faces

In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex.

Dual polyhedron polyhedron whose vertices correspond to the faces of another one

In geometry, any polyhedron is associated with a second dual figure, where the vertices of one correspond to the faces of the other and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all are also geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron.

Octahedron Polyhedron with 8 faces

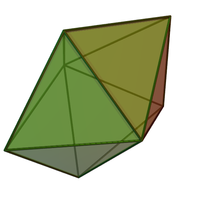
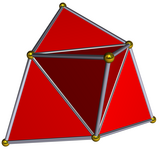
In geometry, an octahedron is a polyhedron with eight faces, twelve edges, and six vertices. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.

A polyhedral compound is a figure that is composed of several polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram.

Simplicial complex

In mathematics, a simplicial complex is a set composed of points, line segments, triangles, and their n-dimensional counterparts. Simplicial complexes should not be confused with the more abstract notion of a simplicial set appearing in modern simplicial homotopy theory. The purely combinatorial counterpart to a simplicial complex is an abstract simplicial complex.

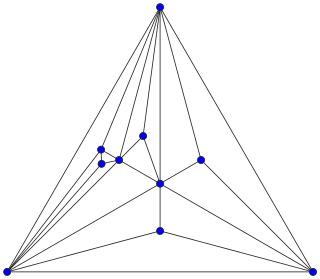
In geometry, the barycentric subdivision is a standard way of dividing an arbitrary convex polygon into triangles, a convex polyhedron into tetrahedra, or, in general, a convex polytope into simplices with the same dimension, by connecting the barycenters of their faces in a specific way.

Rectification (geometry) process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points

In Euclidean geometry, rectification or complete-truncation is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points. The resulting polytope will be bounded by vertex figure facets and the rectified facets of the original polytope.

Runcinated 5-cell

In four-dimensional geometry, a runcinated 5-cell is a convex uniform 4-polytope, being a runcination of the regular 5-cell.

Rectified 5-cell uniform polychoron

In four-dimensional geometry, the rectified 5-cell is a uniform 4-polytope composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10 vertices. Each vertex is surrounded by 3 octahedra and 2 tetrahedra; the vertex figure is a triangular prism.

Great icosahedron Kepler–Poinsot polyhedron

In geometry, the great icosahedron is one of four Kepler-Poinsot polyhedra, with Schläfli symbol {3,5/2} and Coxeter-Dynkin diagram of . It is composed of 20 intersecting triangular faces, having five triangles meeting at each vertex in a pentagrammic sequence.

Truncated 5-cell

In geometry, a truncated 5-cell is a uniform 4-polytope formed as the truncation of the regular 5-cell.

Simple polytope n-dimensional polytope each of whose vertices are adjacent to exactly n edges

In geometry, a d-dimensional simple polytope is a d-dimensional polytope each of whose vertices are adjacent to exactly d edges. The vertex figure of a simple d-polytope is a (d − 1)-simplex.

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the (simple) 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. Branko Grünbaum has called this theorem “the most important and deepest known result on 3-polytopes.”

In geometry and polyhedral combinatorics, the Kleetope of a polyhedron or higher-dimensional convex polytope P is another polyhedron or polytope PK formed by replacing each facet of P with a shallow pyramid. Kleetopes are named after Victor Klee.

References

  1. 1 2 Miller, Ezra; Reiner, Victor; Sturmfels, Bernd, Geometric Combinatorics, IAS/Park City mathematics series, 13, American Mathematical Society, p. 621, ISBN   9780821886953 .
  2. ↑ Koch, Etan; Perles, Micha A. (1976), "Covering efficiency of trees and k-trees", Proceedings of the Seventh Southeastern Conference on Combinatorics, Graph Theory, and Computing (Louisiana State Univ., Baton Rouge, La., 1976), Congressus Numerantium, Winnipeg, Manitoba, Canada: Utilitas Mathematica, 17: 391–420, MR   0457265 . See in particular p. 420.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.