
In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids—liquids and gases. It has several subdisciplines, including aerodynamics and hydrodynamics. Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space and modelling fission weapon detonation.

Mach number is a dimensionless quantity in fluid dynamics representing the ratio of flow velocity past a boundary to the local speed of sound.

A pitottube measures fluid flow velocity. It was invented by a French engineer, Henri Pitot, in the early 18th century, and was modified to its modern form in the mid-19th century by a French scientist, Henry Darcy. It is widely used to determine the airspeed of aircraft; the water speed of boats; and the flow velocity of liquids, air, and gases in industry.

In physics, the Navier–Stokes equations are certain partial differential equations which describe the motion of viscous fluid substances, named after French engineer and physicist Claude-Louis Navier and Anglo-Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).

In fluid dynamics, Bernoulli's principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in static pressure or a decrease in the fluid's potential energy. The principle is named after Daniel Bernoulli who published it in his book Hydrodynamica in 1738. Although Bernoulli deduced that pressure decreases when the flow speed increases, it was Leonhard Euler in 1752 who derived Bernoulli's equation in its usual form. The principle is only applicable for isentropic flows: when the effects of irreversible processes and non-adiabatic processes are small and can be neglected.

In fluid dynamics, the Euler equations are a set of quasilinear partial differential equations governing adiabatic and inviscid flow. They are named after Leonhard Euler. In particular, they correspond to the Navier–Stokes equations with zero viscosity and zero thermal conductivity.
In fluid mechanics or more generally continuum mechanics, incompressible flow refers to a flow in which the material density is constant within a fluid parcel—an infinitesimal volume that moves with the flow velocity. An equivalent statement that implies incompressibility is that the divergence of the flow velocity is zero.

In aviation, airspeed is the speed of an aircraft relative to the air. Among the common conventions for qualifying airspeed are:
Indicated airspeed (IAS) is the airspeed read directly from the airspeed indicator (ASI) on an aircraft, driven by the pitot-static system. It uses the difference between total pressure and static pressure, provided by the system, to either mechanically or electronically measure dynamic pressure. The dynamic pressure includes terms for both density and airspeed. Since the airspeed indicator cannot know the density, it is by design calibrated to assume the sea level standard atmospheric density when calculating airspeed. Since the actual density will vary considerably from this assumed value as the aircraft changes altitude, IAS varies considerably from true airspeed (TAS), the relative velocity between the aircraft and the surrounding air mass. Calibrated airspeed (CAS) is the IAS corrected for instrument and position error.
The pressure coefficient is a dimensionless number which describes the relative pressures throughout a flow field in fluid dynamics. The pressure coefficient is used in aerodynamics and hydrodynamics. Every point in a fluid flow field has its own unique pressure coefficient, .
An orifice plate is a device used for measuring flow rate, for reducing pressure or for restricting flow.

An oblique shock wave is a shock wave that, unlike a normal shock, is inclined with respect to the incident upstream flow direction. It will occur when a supersonic flow encounters a corner that effectively turns the flow into itself and compresses. The upstream streamlines are uniformly deflected after the shock wave. The most common way to produce an oblique shock wave is to place a wedge into supersonic, compressible flow. Similar to a normal shock wave, the oblique shock wave consists of a very thin region across which nearly discontinuous changes in the thermodynamic properties of a gas occur. While the upstream and downstream flow directions are unchanged across a normal shock, they are different for flow across an oblique shock wave.
Rayleigh flow refers to frictionless, non-adiabatic flow through a constant area duct where the effect of heat addition or rejection is considered. Compressibility effects often come into consideration, although the Rayleigh flow model certainly also applies to incompressible flow. For this model, the duct area remains constant and no mass is added within the duct. Therefore, unlike Fanno flow, the stagnation temperature is a variable. The heat addition causes a decrease in stagnation pressure, which is known as the Rayleigh effect and is critical in the design of combustion systems. Heat addition will cause both supersonic and subsonic Mach numbers to approach Mach 1, resulting in choked flow. Conversely, heat rejection decreases a subsonic Mach number and increases a supersonic Mach number along the duct. It can be shown that for calorically perfect flows the maximum entropy occurs at M = 1. Rayleigh flow is named after John Strutt, 3rd Baron Rayleigh.
In fluid mechanics the term static pressure has several uses:
In incompressible fluid dynamics dynamic pressure is the quantity defined by:
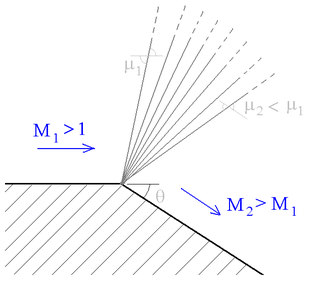
A supersonic expansion fan, technically known as Prandtl–Meyer expansion fan, a two-dimensional simple wave, is a centered expansion process that occurs when a supersonic flow turns around a convex corner. The fan consists of an infinite number of Mach waves, diverging from a sharp corner. When a flow turns around a smooth and circular corner, these waves can be extended backwards to meet at a point.
In fluid dynamics, a moving shock is a shock wave that is travelling through a fluid medium with a velocity relative to the velocity of the fluid already making up the medium. As such, the normal shock relations require modification to calculate the properties before and after the moving shock. A knowledge of moving shocks is important for studying the phenomena surrounding detonation, among other applications.
In physics, the term total pressure may indicate two different quantities, both having the dimensions of a pressure:
In aerodynamics, the normal shock tables are a series of tabulated data listing the various properties before and after the occurrence of a normal shock wave. With a given upstream Mach number, the post-shock Mach number can be calculated along with the pressure, density, temperature, and stagnation pressure ratios. Such tables are useful since the equations used to calculate the properties after a normal shock are cumbersome.
In compressible fluid dynamics, impact pressure is the difference between total pressure and static pressure. In aerodynamics notation, this quantity is denoted as or .























