
In thermodynamics, the specific heat capacity of a substance is the amount of heat that must be added to one unit of mass of the substance in order to cause an increase of one unit in temperature. It is also referred to as massic heat capacity or as the specific heat. More formally it is the heat capacity of a sample of the substance divided by the mass of the sample. The SI unit of specific heat capacity is joule per kelvin per kilogram, J⋅kg−1⋅K−1. For example, the heat required to raise the temperature of 1 kg of water by 1 K is 4184 joules, so the specific heat capacity of water is 4184 J⋅kg−1⋅K−1.

In thermodynamics, the enthalpy of vaporization, also known as the (latent) heat of vaporization or heat of evaporation, is the amount of energy (enthalpy) that must be added to a liquid substance to transform a quantity of that substance into a gas. The enthalpy of vaporization is a function of the pressure and temperature at which the transformation takes place.

In thermodynamics, the thermodynamic free energy is one of the state functions of a thermodynamic system. The change in the free energy is the maximum amount of work that the system can perform in a process at constant temperature, and its sign indicates whether the process is thermodynamically favorable or forbidden. Since free energy usually contains potential energy, it is not absolute but depends on the choice of a zero point. Therefore, only relative free energy values, or changes in free energy, are physically meaningful.

An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics. The requirement of zero interaction can often be relaxed if, for example, the interaction is perfectly elastic or regarded as point-like collisions.
Thermal conduction is the diffusion of thermal energy (heat) within one material or between materials in contact. The higher temperature object has molecules with more kinetic energy; collisions between molecules distributes this kinetic energy until an object has the same kinetic energy throughout. Thermal conductivity, frequently represented by k, is a property that relates the rate of heat loss per unit area of a material to its rate of change of temperature. Essentially, it is a value that accounts for any property of the material that could change the way it conducts heat. Heat spontaneously flows along a temperature gradient. For example, heat is conducted from the hotplate of an electric stove to the bottom of a saucepan in contact with it. In the absence of an opposing external driving energy source, within a body or between bodies, temperature differences decay over time, and thermal equilibrium is approached, temperature becoming more uniform.

In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quantity such as heat diffuses through a given region. Since then, the heat equation and its variants have been found to be fundamental in many parts of both pure and applied mathematics.

Heat capacity or thermal capacity is a physical property of matter, defined as the amount of heat to be supplied to an object to produce a unit change in its temperature. The SI unit of heat capacity is joule per kelvin (J/K).

In thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the useful work obtainable from a closed thermodynamic system at a constant temperature (isothermal). The change in the Helmholtz energy during a process is equal to the maximum amount of work that the system can perform in a thermodynamic process in which temperature is held constant. At constant temperature, the Helmholtz free energy is minimized at equilibrium.

The internal energy of a thermodynamic system is the energy of the system as a state function, measured as the quantity of energy necessary to bring the system from its standard internal state to its present internal state of interest, accounting for the gains and losses of energy due to changes in its internal state, including such quantities as magnetization. It excludes the kinetic energy of motion of the system as a whole and the potential energy of position of the system as a whole, with respect to its surroundings and external force fields. It includes the thermal energy, i.e., the constituent particles' kinetic energies of motion relative to the motion of the system as a whole. The internal energy of an isolated system cannot change, as expressed in the law of conservation of energy, a foundation of the first law of thermodynamics. The notion has been introduced to describe the systems characterized by temperature variations, temperature being added to the set of state parameters, the position variables known in mechanics, in a similar way to potential energy of the conservative fields of force, gravitational and electrostatic. Internal energy changes equal the algebraic sum of the heat transferred and the work done. In systems without temperature changes, potential energy changes equal the work done by/on the system.
The standard enthalpy of reaction for a chemical reaction is the difference between total product and total reactant molar enthalpies, calculated for substances in their standard states. The value can be approximately interpreted in terms of the total of the chemical bond energies for bonds broken and bonds formed.

An isentropic process is an idealized thermodynamic process that is both adiabatic and reversible. The work transfers of the system are frictionless, and there is no net transfer of heat or matter. Such an idealized process is useful in engineering as a model of and basis of comparison for real processes. This process is idealized because reversible processes do not occur in reality; thinking of a process as both adiabatic and reversible would show that the initial and final entropies are the same, thus, the reason it is called isentropic. Thermodynamic processes are named based on the effect they would have on the system. Even though in reality it is not necessarily possible to carry out an isentropic process, some may be approximated as such.
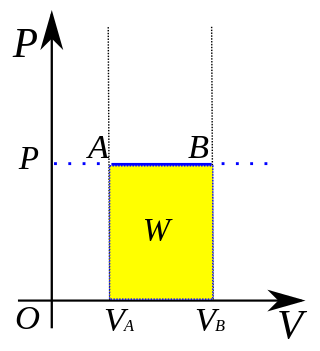
In thermodynamics, an isobaric process is a type of thermodynamic process in which the pressure of the system stays constant: ΔP = 0. The heat transferred to the system does work, but also changes the internal energy (U) of the system. This article uses the physics sign convention for work, where positive work is work done by the system. Using this convention, by the first law of thermodynamics,

In classical statistical mechanics, the equipartition theorem relates the temperature of a system to its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition. The original idea of equipartition was that, in thermal equilibrium, energy is shared equally among all of its various forms; for example, the average kinetic energy per degree of freedom in translational motion of a molecule should equal that in rotational motion.

Thermodynamics is expressed by a mathematical framework of thermodynamic equations which relate various thermodynamic quantities and physical properties measured in a laboratory or production process. Thermodynamics is based on a fundamental set of postulates, that became the laws of thermodynamics.
The Clausius–Clapeyron relation, in chemical thermodynamics, specifies the temperature dependence of pressure, most importantly vapor pressure, at a discontinuous phase transition between two phases of matter of a single constituent. It is named after Rudolf Clausius and Benoît Paul Émile Clapeyron. However, this relation was in fact originally derived by Sadi Carnot in his Reflections on the Motive Power of Fire, which was published in 1824 but largely ignored until it was rediscovered by Clausius, Clapeyron, and Lord Kelvin decades later. Kelvin said of Carnot's argument that "nothing in the whole range of Natural Philosophy is more remarkable than the establishment of general laws by such a process of reasoning."

In thermal physics and thermodynamics, the heat capacity ratio, also known as the adiabatic index, the ratio of specific heats, or Laplace's coefficient, is the ratio of the heat capacity at constant pressure to heat capacity at constant volume. It is sometimes also known as the isentropic expansion factor and is denoted by γ (gamma) for an ideal gas or κ (kappa), the isentropic exponent for a real gas. The symbol γ is used by aerospace and chemical engineers. where C is the heat capacity, the molar heat capacity, and c the specific heat capacity of a gas. The suffixes P and V refer to constant-pressure and constant-volume conditions respectively.

A thermodynamic cycle consists of linked sequences of thermodynamic processes that involve transfer of heat and work into and out of the system, while varying pressure, temperature, and other state variables within the system, and that eventually returns the system to its initial state. In the process of passing through a cycle, the working fluid (system) may convert heat from a warm source into useful work, and dispose of the remaining heat to a cold sink, thereby acting as a heat engine. Conversely, the cycle may be reversed and use work to move heat from a cold source and transfer it to a warm sink thereby acting as a heat pump. If at every point in the cycle the system is in thermodynamic equilibrium, the cycle is reversible. Whether carried out reversible or irreversibly, the net entropy change of the system is zero, as entropy is a state function.
In classical thermodynamics, entropy is a property of a thermodynamic system that expresses the direction or outcome of spontaneous changes in the system. The term was introduced by Rudolf Clausius in the mid-19th century to explain the relationship of the internal energy that is available or unavailable for transformations in form of heat and work. Entropy predicts that certain processes are irreversible or impossible, despite not violating the conservation of energy. The definition of entropy is central to the establishment of the second law of thermodynamics, which states that the entropy of isolated systems cannot decrease with time, as they always tend to arrive at a state of thermodynamic equilibrium, where the entropy is highest. Entropy is therefore also considered to be a measure of disorder in the system.

Thermodynamic databases contain information about thermodynamic properties for substances, the most important being enthalpy, entropy, and Gibbs free energy. Numerical values of these thermodynamic properties are collected as tables or are calculated from thermodynamic datafiles. Data is expressed as temperature-dependent values for one mole of substance at the standard pressure of 101.325 kPa, or 100 kPa. Both of these definitions for the standard condition for pressure are in use.
The porous medium equation, also called the nonlinear heat equation, is a nonlinear partial differential equation taking the form:





























