Inductive logic programming (ILP) is a subfield of symbolic artificial intelligence which uses logic programming as a uniform representation for examples, background knowledge and hypotheses. The term "inductive" here refers to philosophical rather than mathematical induction. Given an encoding of the known background knowledge and a set of examples represented as a logical database of facts, an ILP system will derive a hypothesised logic program which entails all the positive and none of the negative examples.
A Bayesian network is a probabilistic graphical model that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG). While it is one of several forms of causal notation, causal networks are special cases of Bayesian networks. Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor. For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. Given symptoms, the network can be used to compute the probabilities of the presence of various diseases.
Inferences are steps in reasoning, moving from premises to logical consequences; etymologically, the word infer means to "carry forward". Inference is theoretically traditionally divided into deduction and induction, a distinction that in Europe dates at least to Aristotle. Deduction is inference deriving logical conclusions from premises known or assumed to be true, with the laws of valid inference being studied in logic. Induction is inference from particular evidence to a universal conclusion. A third type of inference is sometimes distinguished, notably by Charles Sanders Peirce, contradistinguishing abduction from induction.

In artificial intelligence, symbolic artificial intelligence is the term for the collection of all methods in artificial intelligence research that are based on high-level symbolic (human-readable) representations of problems, logic and search. Symbolic AI used tools such as logic programming, production rules, semantic nets and frames, and it developed applications such as knowledge-based systems, symbolic mathematics, automated theorem provers, ontologies, the semantic web, and automated planning and scheduling systems. The Symbolic AI paradigm led to seminal ideas in search, symbolic programming languages, agents, multi-agent systems, the semantic web, and the strengths and limitations of formal knowledge and reasoning systems.
A graphical model or probabilistic graphical model (PGM) or structured probabilistic model is a probabilistic model for which a graph expresses the conditional dependence structure between random variables. They are commonly used in probability theory, statistics—particularly Bayesian statistics—and machine learning.
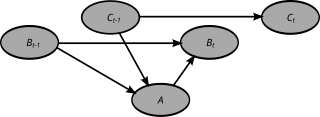
A dynamic Bayesian network (DBN) is a Bayesian network (BN) which relates variables to each other over adjacent time steps.
A Markov logic network (MLN) is a probabilistic logic which applies the ideas of a Markov network to first-order logic, defining probability distributions on possible worlds on any given domain.
Conditional random fields (CRFs) are a class of statistical modeling methods often applied in pattern recognition and machine learning and used for structured prediction. Whereas a classifier predicts a label for a single sample without considering "neighbouring" samples, a CRF can take context into account. To do so, the predictions are modelled as a graphical model, which represents the presence of dependencies between the predictions. What kind of graph is used depends on the application. For example, in natural language processing, "linear chain" CRFs are popular, for which each prediction is dependent only on its immediate neighbours. In image processing, the graph typically connects locations to nearby and/or similar locations to enforce that they receive similar predictions.
Probabilistic logic involves the use of probability and logic to deal with uncertain situations. Probabilistic logic extends traditional logic truth tables with probabilistic expressions. A difficulty of probabilistic logics is their tendency to multiply the computational complexities of their probabilistic and logical components. Other difficulties include the possibility of counter-intuitive results, such as in case of belief fusion in Dempster–Shafer theory. Source trust and epistemic uncertainty about the probabilities they provide, such as defined in subjective logic, are additional elements to consider. The need to deal with a broad variety of contexts and issues has led to many different proposals.
The following outline is provided as an overview of and topical guide to artificial intelligence:
Structured prediction or structured (output) learning is an umbrella term for supervised machine learning techniques that involves predicting structured objects, rather than scalar discrete or real values.
Probabilistic programming (PP) is a programming paradigm in which probabilistic models are specified and inference for these models is performed automatically. It represents an attempt to unify probabilistic modeling and traditional general purpose programming in order to make the former easier and more widely applicable. It can be used to create systems that help make decisions in the face of uncertainty.
Inductive programming (IP) is a special area of automatic programming, covering research from artificial intelligence and programming, which addresses learning of typically declarative and often recursive programs from incomplete specifications, such as input/output examples or constraints.
Action model learning is an area of machine learning concerned with creation and modification of software agent's knowledge about effects and preconditions of the actions that can be executed within its environment. This knowledge is usually represented in logic-based action description language and used as the input for automated planners.

Probabilistic Soft Logic (PSL) is a statistical relational learning (SRL) framework for modeling probabilistic and relational domains. It is applicable to a variety of machine learning problems, such as collective classification, entity resolution, link prediction, and ontology alignment. PSL combines two tools: first-order logic, with its ability to succinctly represent complex phenomena, and probabilistic graphical models, which capture the uncertainty and incompleteness inherent in real-world knowledge. More specifically, PSL uses "soft" logic as its logical component and Markov random fields as its statistical model. PSL provides sophisticated inference techniques for finding the most likely answer (i.e. the maximum a posteriori (MAP) state). The "softening" of the logical formulas makes inference a polynomial time operation rather than an NP-hard operation.
This glossary of artificial intelligence is a list of definitions of terms and concepts relevant to the study of artificial intelligence, its sub-disciplines, and related fields. Related glossaries include Glossary of computer science, Glossary of robotics, and Glossary of machine vision.
The following outline is provided as an overview of and topical guide to machine learning:
In network theory, link prediction is the problem of predicting the existence of a link between two entities in a network. Examples of link prediction include predicting friendship links among users in a social network, predicting co-authorship links in a citation network, and predicting interactions between genes and proteins in a biological network. Link prediction can also have a temporal aspect, where, given a snapshot of the set of links at time , the goal is to predict the links at time . Link prediction is widely applicable. In e-commerce, link prediction is often a subtask for recommending items to users. In the curation of citation databases, it can be used for record deduplication. In bioinformatics, it has been used to predict protein-protein interactions (PPI). It is also used to identify hidden groups of terrorists and criminals in security related applications.
In network theory, collective classification is the simultaneous prediction of the labels for multiple objects, where each label is predicted using information about the object's observed features, the observed features and labels of its neighbors, and the unobserved labels of its neighbors. Collective classification problems are defined in terms of networks of random variables, where the network structure determines the relationship between the random variables. Inference is performed on multiple random variables simultaneously, typically by propagating information between nodes in the network to perform approximate inference. Approaches that use collective classification can make use of relational information when performing inference. Examples of collective classification include predicting attributes of individuals in a social network, classifying webpages in the World Wide Web, and inferring the research area of a paper in a scientific publication dataset.


