In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic on the whole complex plane. Typical examples of entire functions are polynomials and the exponential function, and any finite sums, products and compositions of these, such as the trigonometric functions sine and cosine and their hyperbolic counterparts sinh and cosh, as well as derivatives and integrals of entire functions such as the error function. If an entire function has a root at , then , taking the limit value at , is an entire function. On the other hand, the natural logarithm, the reciprocal function, and the square root are all not entire functions, nor can they be continued analytically to an entire function.
In number theory, a multiplicative function is an arithmetic function f(n) of a positive integer n with the property that f(1) = 1 and

In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of definition of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where the infinite series representation which initially defined the function becomes divergent.
In the mathematical field of real analysis, the monotone convergence theorem is any of a number of related theorems proving the convergence of monotonic sequences that are also bounded. Informally, the theorems state that if a sequence is increasing and bounded above by a supremum, then the sequence will converge to the supremum; in the same way, if a sequence is decreasing and is bounded below by an infimum, it will converge to the infimum.
In mathematics, a generating function is a way of encoding an infinite sequence of numbers by treating them as the coefficients of a formal power series. This series is called the generating function of the sequence. Unlike an ordinary series, the formal power series is not required to converge: in fact, the generating function is not actually regarded as a function, and the "variable" remains an indeterminate. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general linear recurrence problem. One can generalize to formal power series in more than one indeterminate, to encode information about infinite multi-dimensional arrays of numbers.
In order theory, a field of mathematics, an incidence algebra is an associative algebra, defined for every locally finite partially ordered set and commutative ring with unity. Subalgebras called reduced incidence algebras give a natural construction of various types of generating functions used in combinatorics and number theory.
In mathematics, the falling factorial is defined as the polynomial
In mathematics, in particular in algebraic topology, differential geometry and algebraic geometry, the Chern classes are characteristic classes associated with complex vector bundles. They have since become fundamental concepts in many branches of mathematics and physics, such as string theory, Chern–Simons theory, knot theory, Gromov–Witten invariants. Chern classes were introduced by Shiing-Shen Chern (1946).
In mathematics, a Dirichlet series is any series of the form
In combinatorial mathematics, the necklace polynomial, or Moreau's necklace-counting function, introduced by C. Moreau (1872), counts the number of distinct necklaces of n colored beads chosen out of α available colors, arranged in a cycle. Unlike the usual problem of graph coloring, the necklaces are assumed to be aperiodic, and counted up to rotation, but without flipping over. This counting function also describes the dimensions in a free Lie algebra and the number of irreducible polynomials over a finite field.
The Basel problem is a problem in mathematical analysis with relevance to number theory, concerning an infinite sum of inverse squares. It was first posed by Pietro Mengoli in 1650 and solved by Leonhard Euler in 1734, and read on 5 December 1735 in The Saint Petersburg Academy of Sciences. Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate fame when he was twenty-eight. Euler generalised the problem considerably, and his ideas were taken up more than a century later by Bernhard Riemann in his seminal 1859 paper "On the Number of Primes Less Than a Given Magnitude", in which he defined his zeta function and proved its basic properties. The problem is named after Basel, hometown of Euler as well as of the Bernoulli family who unsuccessfully attacked the problem.
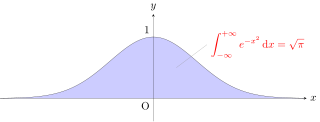
The Gaussian integral, also known as the Euler–Poisson integral, is the integral of the Gaussian function over the entire real line. Named after the German mathematician Carl Friedrich Gauss, the integral is

In mathematics, a Lambert series, named for Johann Heinrich Lambert, is a series taking the form

The dyadic transformation is the mapping
In mathematics, especially in combinatorics, Stirling numbers of the first kind arise in the study of permutations. In particular, the Stirling numbers of the first kind count permutations according to their number of cycles.
In probability theory, calculation of the sum of normally distributed random variables is an instance of the arithmetic of random variables.
The statistics of random permutations, such as the cycle structure of a random permutation are of fundamental importance in the analysis of algorithms, especially of sorting algorithms, which operate on random permutations. Suppose, for example, that we are using quickselect to select a random element of a random permutation. Quickselect will perform a partial sort on the array, as it partitions the array according to the pivot. Hence a permutation will be less disordered after quickselect has been performed. The amount of disorder that remains may be analysed with generating functions. These generating functions depend in a fundamental way on the generating functions of random permutation statistics. Hence it is of vital importance to compute these generating functions.
In statistical mechanics, the Griffiths inequality, sometimes also called Griffiths–Kelly–Sherman inequality or GKS inequality, named after Robert B. Griffiths, is a correlation inequality for ferromagnetic spin systems. Informally, it says that in ferromagnetic spin systems, if the 'a-priori distribution' of the spin is invariant under spin flipping, the correlation of any monomial of the spins is non-negative; and the two point correlation of two monomial of the spins is non-negative.
In analytic number theory, a Dirichlet series, or Dirichlet generating function (DGF), of a sequence is a common way of understanding and summing arithmetic functions in a meaningful way. A little known, or at least often forgotten about, way of expressing formulas for arithmetic functions and their summatory functions is to perform an integral transform that inverts the operation of forming the DGF of a sequence. This inversion is analogous to performing an inverse Z-transform to the generating function of a sequence to express formulas for the series coefficients of a given ordinary generating function.



























































































