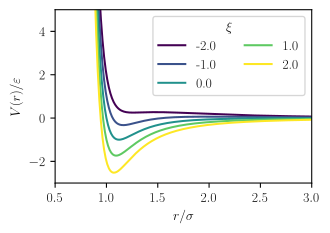
The Stockmayer potential is a mathematical model for representing the interactions between pairs of atoms or molecules. It is defined as a Lennard-Jones potential with a point electric dipole moment.
A Stockmayer liquid consists of a collection of spheres with point dipoles embedded at the centre of each. These spheres interact both by Lennard-Jones and dipolar interactions. In the absence of the point dipoles, the spheres face no rotational friction and the translational dynamics of such LJ spheres have been studied in detail. This system, therefore, provides a simple model where the only source of rotational friction is dipolar interactions. [1]
The interaction potential may be written as
where the parameters and are related to dispersion strength and particle size respectively, just as in the Mie potential or Lennard-Jones potential, which is the source of the first term, is the dipole moment of species , and is a parameter describing the relative orientation of the two dipoles, which may vary between -2 and 2. [2]






