In mathematical physics, a lattice model is a mathematical model of a physical system that is defined on a lattice, as opposed to a continuum, such as the continuum of space or spacetime. Lattice models originally occurred in the context of condensed matter physics, where the atoms of a crystal automatically form a lattice. Currently, lattice models are quite popular in theoretical physics, for many reasons. Some models are exactly solvable, and thus offer insight into physics beyond what can be learned from perturbation theory. Lattice models are also ideal for study by the methods of computational physics, as the discretization of any continuum model automatically turns it into a lattice model. The exact solution to many of these models includes the presence of solitons. Techniques for solving these include the inverse scattering transform and the method of Lax pairs, the Yang–Baxter equation and quantum groups. The solution of these models has given insights into the nature of phase transitions, magnetization and scaling behaviour, as well as insights into the nature of quantum field theory. Physical lattice models frequently occur as an approximation to a continuum theory, either to give an ultraviolet cutoff to the theory to prevent divergences or to perform numerical computations. An example of a continuum theory that is widely studied by lattice models is the QCD lattice model, a discretization of quantum chromodynamics. However, digital physics considers nature fundamentally discrete at the Planck scale, which imposes upper limit to the density of information, aka Holographic principle. More generally, lattice gauge theory and lattice field theory are areas of study. Lattice models are also used to simulate the structure and dynamics of polymers.
The Ising model, named after the physicists Ernst Ising and Wilhelm Lenz, is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that represent magnetic dipole moments of atomic "spins" that can be in one of two states. The spins are arranged in a graph, usually a lattice, allowing each spin to interact with its neighbors. Neighboring spins that agree have a lower energy than those that disagree; the system tends to the lowest energy but heat disturbs this tendency, thus creating the possibility of different structural phases. The model allows the identification of phase transitions as a simplified model of reality. The two-dimensional square-lattice Ising model is one of the simplest statistical models to show a phase transition.

The Drude model of electrical conduction was proposed in 1900 by Paul Drude to explain the transport properties of electrons in materials. Basically, Ohm's law was well established and stated that the current J and voltage V driving the current are related to the resistance R of the material. The inverse of the resistance is known as the conductance. When we consider a metal of unit length and unit cross sectional area, the conductance is known as the conductivity, which is the inverse of resistivity. The Drude model attempts to explain the resistivity of a conductor in terms of the scattering of electrons by the relatively immobile ions in the metal that act like obstructions to the flow of electrons.
The classical XY model is a lattice model of statistical mechanics. In general, the XY model can be seen as a specialization of Stanley's n-vector model for n = 2.
In condensed matter physics, the Fermi surface is the surface in reciprocal space which separates occupied from unoccupied electron states at zero temperature. The shape of the Fermi surface is derived from the periodicity and symmetry of the crystalline lattice and from the occupation of electronic energy bands. The existence of a Fermi surface is a direct consequence of the Pauli exclusion principle, which allows a maximum of one electron per quantum state. The study of the Fermi surfaces of materials is called fermiology.
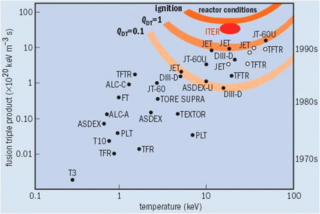
The Lawson criterion is a figure of merit used in nuclear fusion research. It compares the rate of energy being generated by fusion reactions within the fusion fuel to the rate of energy losses to the environment. When the rate of production is higher than the rate of loss, the system will produce net energy. If enough of that energy is captured by the fuel, the system will become self-sustaining and is said to be ignited.

The Hubbard model is an approximate model used to describe the transition between conducting and insulating systems. It is particularly useful in solid-state physics. The model is named for John Hubbard.

In quantum mechanics, a two-state system is a quantum system that can exist in any quantum superposition of two independent quantum states. The Hilbert space describing such a system is two-dimensional. Therefore, a complete basis spanning the space will consist of two independent states. Any two-state system can also be seen as a qubit.
In chemistry and physics, the exchange interaction or exchange splitting is a quantum mechanical effect that only occurs between identical particles. Despite sometimes being called an exchange force in an analogy to classical force, it is not a true force as it lacks a force carrier.
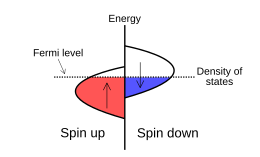
Edmund Clifton Stoner FRS was a British theoretical physicist. He is principally known for his work on the origin and nature of itinerant ferromagnetism, including the collective electron theory of ferromagnetism and the Stoner criterion for ferromagnetism. Stoner made significant contributions to the electron configurations in the periodic table.

In solid-state physics, the t-J model is a model first derived in 1977 from the Hubbard model by Józef Spałek to explain antiferromagnetic properties of the Mott insulators and taking into account experimental results about the strength of electron-electron repulsion in this materials. The model consider the materials as a lattice with atoms in the knots (sites) and just one or two external electrons moving among them, like in the basic Hubbard model. That difference is in supposing electrons being strongly-correlated, that means electrons are very sensible to reciprocal coulombic repulsion, and so are more constrained to avoid occupying lattice's sites already occupied by another electron. In the basic Hubbard model, the repulsion, indicated with U, can be small and also null, and electrons are freer to jump from one site to another. In the t-J model, instead of U, there is the parameter J, function of the ratio t/U, so the name.
The Anderson impurity model, named after Philip Warren Anderson, is a Hamiltonian that is used to describe magnetic impurities embedded in metals. It is often applied to the description of Kondo effect-type problems, such as heavy fermion systems and Kondo insulators. In its simplest form, the model contains a term describing the kinetic energy of the conduction electrons, a two-level term with an on-site Coulomb repulsion that models the impurity energy levels, and a hybridization term that couples conduction and impurity orbitals. For a single impurity, the Hamiltonian takes the form
A schema is a template in computer science used in the field of genetic algorithms that identifies a subset of strings with similarities at certain string positions. Schemata are a special case of cylinder sets, forming a basis for a product topology on strings. In other words, schemata can be used to generate a topology on a space of strings.
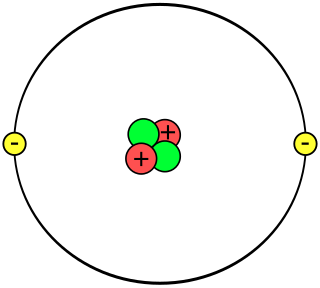
A helium atom is an atom of the chemical element helium. Helium is composed of two electrons bound by the electromagnetic force to a nucleus containing two protons along with either one or two neutrons, depending on the isotope, held together by the strong force. Unlike for hydrogen, a closed-form solution to the Schrödinger equation for the helium atom has not been found. However, various approximations, such as the Hartree–Fock method, can be used to estimate the ground state energy and wavefunction of the atom.
Dynamical mean-field theory (DMFT) is a method to determine the electronic structure of strongly correlated materials. In such materials, the approximation of independent electrons, which is used in density functional theory and usual band structure calculations, breaks down. Dynamical mean-field theory, a non-perturbative treatment of local interactions between electrons, bridges the gap between the nearly free electron gas limit and the atomic limit of condensed-matter physics.
In the theory of quantum communication, an amplitude damping channel is a quantum channel that models physical processes such as spontaneous emission. A natural process by which this channel can occur is a spin chain through which a number of spin states, coupled by a time independent Hamiltonian, can be used to send a quantum state from one location to another. The resulting quantum channel ends up being identical to an amplitude damping channel, for which the quantum capacity, the classical capacity and the entanglement assisted classical capacity of the quantum channel can be evaluated.
In statistical mechanics, the Griffiths inequality, sometimes also called Griffiths–Kelly–Sherman inequality or GKS inequality, named after Robert B. Griffiths, is a correlation inequality for ferromagnetic spin systems. Informally, it says that in ferromagnetic spin systems, if the 'a-priori distribution' of the spin is invariant under spin flipping, the correlation of any monomial of the spins is non-negative; and the two point correlation of two monomial of the spins is non-negative.
Many-body localization (MBL) is a dynamical phenomenon which leads to the breakdown of equilibrium statistical mechanics in isolated many-body systems. Such systems never reach local thermal equilibrium, and retain local memory of their initial conditions for infinite times. One can still define a notion of phase structure in these out-of-equilibrium systems. Strikingly, MBL can even enable new kinds of exotic orders that are disallowed in thermal equilibrium – a phenomenon that goes by the name of localization-protected quantum order (LPQO) or eigenstate order.
Exact diagonalization (ED) is a numerical technique used in physics to determine the eigenstates and energy eigenvalues of a quantum Hamiltonian. In this technique, a Hamiltonian for a discrete, finite system is expressed in matrix form and diagonalized using a computer. Exact diagonalization is only feasible for systems with a few tens of particles, due to the exponential growth of the Hilbert space dimension with the size of the quantum system. It is frequently employed to study lattice models, including the Hubbard model, Ising model, Heisenberg model, t-J model, and SYK model.
The two-dimensional critical Ising model is the critical limit of the Ising model in two dimensions. It is a two-dimensional conformal field theory whose symmetry algebra is the Virasoro algebra with the central charge . Correlation functions of the spin and energy operators are described by the minimal model. While the minimal model has been exactly solved, see also, e.g., the article on Ising critical exponents, the solution does not cover other observables such as connectivities of clusters.