
In mathematics and computational geometry, a Delaunay triangulation for a given set P of discrete points in a general position is a triangulation DT(P) such that no point in P is inside the circumcircle of any triangle in DT(P). Delaunay triangulations maximize the minimum of all the angles of the triangles in the triangulation; they tend to avoid sliver triangles. The triangulation is named after Boris Delaunay for his work on this topic from 1934.
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational geometry. While modern computational geometry is a recent development, it is one of the oldest fields of computing with a history stretching back to antiquity.

In mathematics, a Voronoi diagram is a partition of a plane into regions close to each of a given set of objects. In the simplest case, these objects are just finitely many points in the plane. For each seed there is a corresponding region, called a Voronoi cell, consisting of all points of the plane closer to that seed than to any other. The Voronoi diagram of a set of points is dual to that set's Delaunay triangulation.
The point location problem is a fundamental topic of computational geometry. It finds applications in areas that deal with processing geometrical data: computer graphics, geographic information systems (GIS), motion planning, and computer aided design (CAD).
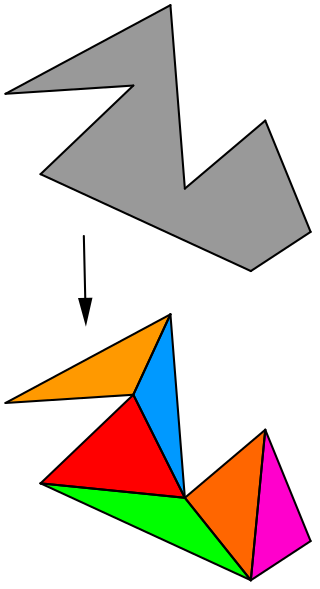
In computational geometry, polygon triangulation is the partition of a polygonal area P into a set of triangles, i.e., finding a set of triangles with pairwise non-intersecting interiors whose union is P.

In geometry, an arrangement of lines is the subdivision of the plane formed by a collection of lines. Bounds on the complexity of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.

A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.

A triangulation of a set of points in the Euclidean space is a simplicial complex that covers the convex hull of , and whose vertices belong to . In the plane, triangulations are made up of triangles, together with their edges and vertices. Some authors require that all the points of are vertices of its triangulations. In this case, a triangulation of a set of points in the plane can alternatively be defined as a maximal set of non-crossing edges between points of . In the plane, triangulations are special cases of planar straight-line graphs.
The art gallery problem or museum problem is a well-studied visibility problem in computational geometry. It originates from the following real-world problem:
In computational complexity, problems that are in the complexity class NP but are neither in the class P nor NP-complete are called NP-intermediate, and the class of such problems is called NPI. Ladner's theorem, shown in 1975 by Richard E. Ladner, is a result asserting that, if P ≠ NP, then NPI is not empty; that is, NP contains problems that are neither in P nor NP-complete. Since it is also true that if NPI problems exist, then P ≠ NP, it follows that P = NP if and only if NPI is empty.

In Euclidean plane geometry, a pseudotriangle (pseudo-triangle) is the simply connected subset of the plane that lies between any three mutually tangent convex sets. A pseudotriangulation (pseudo-triangulations) is a partition of a region of the plane into pseudotriangles, and a pointed pseudotriangulation is a pseudotriangulation in which at each vertex the incident edges span an angle of less than π.
Algorithms that construct convex hulls of various objects have a broad range of applications in mathematics and computer science.

In geometry, a polygon P in the plane is called monotone with respect to a straight line L, if every line orthogonal to L intersects the boundary of P at most twice.

In geometry, a polygonal chain is a connected series of line segments. More formally, a polygonal chain is a curve specified by a sequence of points called its vertices. The curve itself consists of the line segments connecting the consecutive vertices.
In computational geometry and computer science, the minimum-weight triangulation problem is the problem of finding a triangulation of minimal total edge length. That is, an input polygon or the convex hull of an input point set must be subdivided into triangles that meet edge-to-edge and vertex-to-vertex, in such a way as to minimize the sum of the perimeters of the triangles. The problem is NP-hard for point set inputs, but may be approximated to any desired degree of accuracy. For polygon inputs, it may be solved exactly in polynomial time. The minimum weight triangulation has also sometimes been called the optimal triangulation.
David Mount is a professor at the University of Maryland, College Park department of computer science whose research is in computational geometry.
In computational geometry, a constrained Delaunay triangulation is a generalization of the Delaunay triangulation that forces certain required segments into the triangulation as edges, unlike the Delaunay triangulation itself which is based purely on the position of a given set of vertices without regard to how they should be connected by edges. It can be computed efficiently and has applications in geographic information systems and in mesh generation.
In computational complexity theory, and more specifically in the analysis of algorithms with integer data, the transdichotomous model is a variation of the random access machine in which the machine word size is assumed to match the problem size. The model was proposed by Michael Fredman and Dan Willard, who chose its name "because the dichotomy between the machine model and the problem size is crossed in a reasonable manner."

In computational geometry, a greedy geometric spanner is an undirected graph whose distances approximate the Euclidean distances among a finite set of points in a Euclidean space. The vertices of the graph represent these points. The edges of the spanner are selected by a greedy algorithm that includes an edge whenever its two endpoints are not connected by a short path of shorter edges. The greedy spanner was first described in the PhD thesis of Gautam Das and conference paper and subsequent journal paper by Ingo Althöfer et al. These sources also credited Marshall Bern (unpublished) with the independent discovery of the same construction.
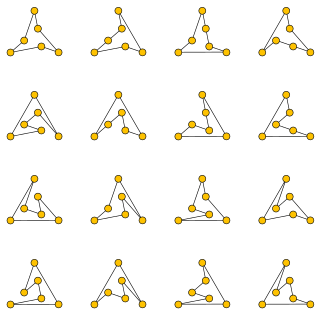
In computational geometry, a polygonalization of a finite set of points in the Euclidean plane is a simple polygon with the given points as its vertices. A polygonalization may also be called a polygonization, simple polygonalization, Hamiltonian polygon, non-crossing Hamiltonian cycle, or crossing-free straight-edge spanning cycle.











