Related Research Articles
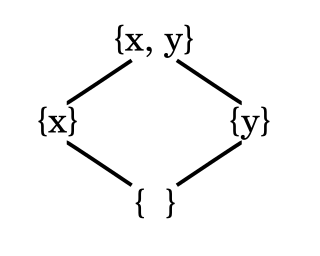
In order theory, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction. Concretely, for a partially ordered set one represents each element of as a vertex in the plane and draws a line segment or curve that goes upward from one vertex to another vertex whenever covers . These curves may cross each other but must not touch any vertices other than their endpoints. Such a diagram, with labeled vertices, uniquely determines its partial order.

Erik D. Demaine is a Canadian-American professor of computer science at the Massachusetts Institute of Technology and a former child prodigy.

In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union. That is, the family of cographs is the smallest class of graphs that includes K1 and is closed under complementation and disjoint union.
The graph isomorphism problem is the computational problem of determining whether two finite graphs are isomorphic.
In graph theory, the treewidth of an undirected graph is an integer number which specifies, informally, how far the graph is from being a tree. The smallest treewidth is 1; the graphs with treewidth 1 are exactly the trees and the forests. An example of graphs with treewidth at most 2 are the series–parallel graphs. The maximal graphs with treewidth exactly k are called k-trees, and the graphs with treewidth at most k are called partial k-trees. Many other well-studied graph families also have bounded treewidth.

In graph theory, a book embedding is a generalization of planar embedding of a graph to embeddings in a book, a collection of half-planes all having the same line as their boundary. Usually, the vertices of the graph are required to lie on this boundary line, called the spine, and the edges are required to stay within a single half-plane. The book thickness of a graph is the smallest possible number of half-planes for any book embedding of the graph. Book thickness is also called pagenumber, stacknumber or fixed outerthickness. Book embeddings have also been used to define several other graph invariants including the pagewidth and book crossing number.
In computational complexity, problems that are in the complexity class NP but are neither in the class P nor NP-complete are called NP-intermediate, and the class of such problems is called NPI. Ladner's theorem, shown in 1975 by Richard E. Ladner, is a result asserting that, if P ≠ NP, then NPI is not empty; that is, NP contains problems that are neither in P nor NP-complete. Since it is also true that if NPI problems exist, then P ≠ NP, it follows that P = NP if and only if NPI is empty.
In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity.
William Lawrence Kocay is a Canadian professor at the department of computer science at St. Paul's College of the University of Manitoba and a graph theorist. He is known for his work in graph algorithms and the reconstruction conjecture and is affectionately referred to as "Wild Bill" by his students. Bill Kocay is a former managing editor of Ars Combinatoria, a Canadian journal of combinatorial mathematics, is a founding fellow of the Institute of Combinatorics and its Applications.
In graph theory and theoretical computer science, the longest path problem is the problem of finding a simple path of maximum length in a given graph. A path is called simple if it does not have any repeated vertices; the length of a path may either be measured by its number of edges, or by the sum of the weights of its edges. In contrast to the shortest path problem, which can be solved in polynomial time in graphs without negative-weight cycles, the longest path problem is NP-hard and the decision version of the problem, which asks whether a path exists of at least some given length, is NP-complete. This means that the decision problem cannot be solved in polynomial time for arbitrary graphs unless P = NP. Stronger hardness results are also known showing that it is difficult to approximate. However, it has a linear time solution for directed acyclic graphs, which has important applications in finding the critical path in scheduling problems.

In combinatorial mathematics, a separable permutation is a permutation that can be obtained from the trivial permutation 1 by direct sums and skew sums. Separable permutations may be characterized by the forbidden permutation patterns 2413 and 3142; they are also the permutations whose permutation graphs are cographs and the permutations that realize the series-parallel partial orders. It is possible to test in polynomial time whether a given separable permutation is a pattern in a larger permutation, or to find the longest common subpattern of two separable permutations.

In geometric graph theory, a branch of mathematics, a matchstick graph is a graph that can be drawn in the plane in such a way that its edges are line segments with length one that do not cross each other. That is, it is a graph that has an embedding which is simultaneously a unit distance graph and a plane graph. For this reason, matchstick graphs have also been called planar unit-distance graphs. Informally, matchstick graphs can be made by placing noncrossing matchsticks on a flat surface, hence the name.
Derek Gordon Corneil is a Canadian mathematician and computer scientist, a professor emeritus of computer science at the University of Toronto, and an expert in graph algorithms and graph theory.
In graph drawing, a universal point set of order n is a set S of points in the Euclidean plane with the property that every n-vertex planar graph has a straight-line drawing in which the vertices are all placed at points of S.

An arc diagram is a style of graph drawing, in which the vertices of a graph are placed along a line in the Euclidean plane, with edges being drawn as semicircles in one or both of the two halfplanes bounded by the line, or as smooth curves formed by sequences of semicircles. In some cases, line segments of the line itself are also allowed as edges, as long as they connect only vertices that are consecutive along the line. Variations of this drawing style in which the semicircles are replaced by convex curves of some other type are also commonly called arc diagrams.

In graph drawing, an upward planar drawing of a directed acyclic graph is an embedding of the graph into the Euclidean plane, in which the edges are represented as non-crossing monotonic upwards curves. That is, the curve representing each edge should have the property that every horizontal line intersects it in at most one point, and no two edges may intersect except at a shared endpoint. In this sense, it is the ideal case for layered graph drawing, a style of graph drawing in which edges are monotonic curves that may cross, but in which crossings are to be minimized.
In graph drawing styles that represent the edges of a graph by polylines, it is desirable to minimize the number of bends per edge or the total number of bends in a drawing. Bend minimization is the algorithmic problem of finding a drawing that minimizes these quantities.
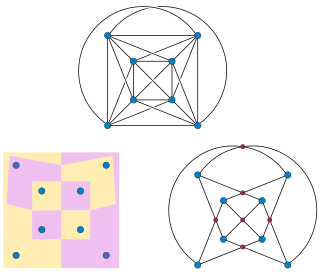
In graph theory, a branch of mathematics, a map graph is an undirected graph formed as the intersection graph of finitely many simply connected and internally disjoint regions of the Euclidean plane. The map graphs include the planar graphs, but are more general. Any number of regions can meet at a common corner, and when they do the map graph will contain a clique connecting the corresponding vertices, unlike planar graphs in which the largest cliques have only four vertices. Another example of a map graph is the king's graph, a map graph of the squares of the chessboard connecting pairs of squares between which the chess king can move.
In geometric graph theory, and the theory of structural rigidity, a parallel redrawing of a graph drawing with straight edges in the Euclidean plane or higher-dimensional Euclidean space is another drawing of the same graph such that all edges of the second drawing are parallel to their corresponding edges in the first drawing. A parallel morph of a graph is a continuous family of drawings, all parallel redrawings of each other.
References
- ↑ Faculty profile Archived 2013-07-22 at the Wayback Machine , University of Waterloo, retrieved 2013-10-16.
- ↑ Anna Lubiw at the Mathematics Genealogy Project
- ↑ "Maths star from outside the fold", Times Higher Education , March 29, 2002.
- ↑ Demaine, Demaine & Lubiw (1999); O'Rourke, Joseph (2013), How to Fold It, Cambridge University Press, p. 144, ISBN 9781139498548 .
- ↑ Hutton & Lubiw (1996); Di Battista, Giuseppe; Eades, Peter; Tamassia, Roberto; Tollis, Ioannis G. (1998), "Optimal Upward Planarity Testing of Single-Source Digraphs", Graph Drawing: Algorithms for the Visualization of Graphs, Prentice Hall, pp. 195–200, ISBN 978-0-13-301615-4 .
- ↑ Bose, Buss & Lubiw (1998); Brignall, Robert (2010), "A survey of simple permutations", in Linton, Steve; Ruškuc, Nik; Vatter, Vincent (eds.), Permutation Patterns, London Mathematical Society Lecture Note Series, vol. 376, Cambridge University Press, pp. 41–66, ISBN 9781139488846, MR 2732823 . See in particular pp. 61–62.
- ↑ Lubiw (1981); Babai, László (1995), "Automorphism groups, isomorphism, reconstruction", Handbook of combinatorics, Vol. 1, 2 (PDF), Amsterdam: Elsevier, pp. 1447–1540, MR 1373683,
A surprising result of Anna Lubiw asserts that the following problem is NP-complete: Does a given permutation group have a fixed-point-free element?
. - ↑ ACM Distinguished member page: http://awards.acm.org/award_winners/lubiw_2950848.cfm
- ↑ "Love of music guides fledgling ensemble", Kitchener Record, November 29, 2005.
- ↑ About the orchestra Archived 2013-06-05 at the Wayback Machine , Univ. of Waterloo, retrieved 2013-10-16.