
In geometry, a polyhedron is a three-dimensional figure with flat polygonal faces, straight edges and sharp corners or vertices.

Origami is the Japanese art of paper folding. In modern usage, the word "origami" is often used as an inclusive term for all folding practices, regardless of their culture of origin. The goal is to transform a flat square sheet of paper into a finished sculpture through folding and sculpting techniques. Modern origami practitioners generally discourage the use of cuts, glue, or markings on the paper. Origami folders often use the Japanese word kirigami to refer to designs which use cuts.
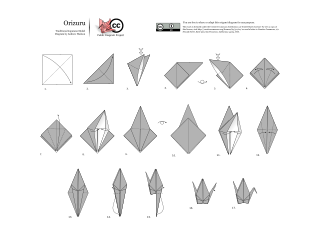
The Yoshizawa–Randlett system is a diagramming system used to describe the folds of origami models. Many origami books begin with a description of basic origami techniques which are used to construct the models. There are also a number of standard bases which are commonly used as a first step in construction. Models are typically classified as requiring low, intermediate or high skill depending on the complexity of the techniques involved in the construction.

The discipline of origami or paper folding has received a considerable amount of mathematical study. Fields of interest include a given paper model's flat-foldability, and the use of paper folds to solve mathematical equations up to the third order.
The Huzita–Justin axioms or Huzita–Hatori axioms are a set of rules related to the mathematical principles of origami, describing the operations that can be made when folding a piece of paper. The axioms assume that the operations are completed on a plane, and that all folds are linear. These are not a minimal set of axioms but rather the complete set of possible single folds.

Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object.
In mathematics, singularity theory studies spaces that are almost manifolds, but not quite. A string can serve as an example of a one-dimensional manifold, if one neglects its thickness. A singularity can be made by balling it up, dropping it on the floor, and flattening it. In some places the flat string will cross itself in an approximate "X" shape. The points on the floor where it does this are one kind of singularity, the double point: one bit of the floor corresponds to more than one bit of string. Perhaps the string will also touch itself without crossing, like an underlined "U". This is another kind of singularity. Unlike the double point, it is not stable, in the sense that a small push will lift the bottom of the "U" away from the "underline".

In geometry, a net of a polyhedron is an arrangement of non-overlapping edge-joined polygons in the plane which can be folded to become the faces of the polyhedron. Polyhedral nets are a useful aid to the study of polyhedra and solid geometry in general, as they allow for physical models of polyhedra to be constructed from material such as thin cardboard.

Robert James Lang is an American physicist who is also one of the foremost origami artists and theorists in the world. He is known for his complex and elegant designs, most notably of insects and animals. He has studied the mathematics of origami and used computers to study the theories behind origami. He has made great advances in making real-world applications of origami to engineering problems.

In geometry, a flexible polyhedron is a polyhedral surface without any boundary edges, whose shape can be continuously changed while keeping the shapes of all of its faces unchanged. The Cauchy rigidity theorem shows that in dimension 3 such a polyhedron cannot be convex.

Kawasaki's theorem or Kawasaki–Justin theorem is a theorem in the mathematics of paper folding that describes the crease patterns with a single vertex that may be folded to form a flat figure. It states that the pattern is flat-foldable if and only if alternatingly adding and subtracting the angles of consecutive folds around the vertex gives an alternating sum of zero. Crease patterns with more than one vertex do not obey such a simple criterion, and are NP-hard to fold.

Rigid origami is a branch of origami which is concerned with folding structures using flat rigid sheets joined by hinges. That is, unlike in traditional origami, the panels of the paper cannot be bent during the folding process; they must remain flat at all times, and the paper only folded along its hinges. A rigid origami model would still be foldable if it was made from glass sheets with hinges in place of its crease lines.
In the mathematics of paper folding, map folding and stamp folding are two problems of counting the number of ways that a piece of paper can be folded. In the stamp folding problem, the paper is a strip of stamps with creases between them, and the folds must lie on the creases. In the map folding problem, the paper is a map, divided by creases into rectangles, and the folds must again lie only along these creases.

In mechanical engineering, Yoshimura buckling is a triangular mesh buckling pattern found in thin-walled cylinders under compression along the axis of the cylinder, producing a corrugated shape resembling the Schwarz lantern. The same pattern can be seen on the sleeves of Mona Lisa.

Alexander Nikolaevich Varchenko is a Soviet and Russian mathematician working in geometry, topology, combinatorics and mathematical physics.
Geometric Folding Algorithms: Linkages, Origami, Polyhedra is a monograph on the mathematics and computational geometry of mechanical linkages, paper folding, and polyhedral nets, by Erik Demaine and Joseph O'Rourke. It was published in 2007 by Cambridge University Press (ISBN 978-0-521-85757-4). A Japanese-language translation by Ryuhei Uehara was published in 2009 by the Modern Science Company (ISBN 978-4-7649-0377-7).

A History of Folding in Mathematics: Mathematizing the Margins is a book in the history of mathematics on the mathematics of paper folding. It was written by Michael Friedman and published in 2018 by Birkhäuser as volume 59 of their Historical Studies series.
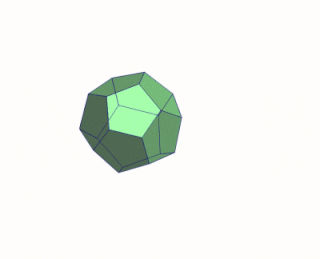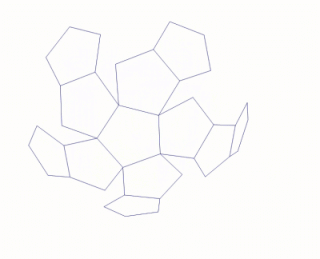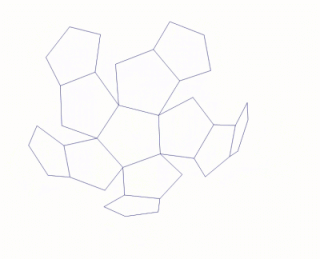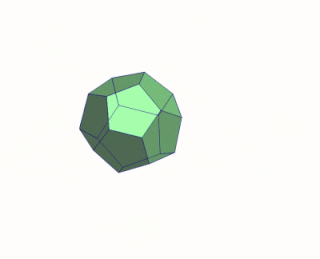
In the geometry of convex polyhedra, blooming or continuous blooming is a continuous three-dimensional motion of the surface of the polyhedron, cut to form a polyhedral net, from the polyhedron into a flat and non-self-overlapping placement of the net in a plane. As in rigid origami, the polygons of the net must remain individually flat throughout the motion, and are not allowed to intersect or cross through each other. A blooming, reversed to go from the flat net to a polyhedron, can be thought of intuitively as a way to fold the polyhedron from a paper net without bending the paper except at its designated creases.
Geometric Origami is a book on the mathematics of paper folding, focusing on the ability to simulate and extend classical straightedge and compass constructions using origami. It was written by Austrian mathematician Robert Geretschläger and published by Arbelos Publishing in 2008. The Basic Library List Committee of the Mathematical Association of America has suggested its inclusion in undergraduate mathematics libraries.
Arnold's Problems is a book edited by Vladimir Arnold containing 861 mathematical problems, from many different areas of mathematics. The book was based on Arnold's seminars at Moscow State University. The problems were created over his decades-long career, and are sorted chronologically. It was published in Russian as Задачи Арнольда in 2000, and in a translated and revised English edition in 2004. The book is divided into two parts: formulations of the problems, and comments upon them by 59 mathematicians. This is the largest part of the book. There are also long outlines for programs of research.














