Bricard octahedron

Last updated
Bricard octahedron with a rectangle as its equator. The axis of symmetry passes perpendicularly through the center of the rectangle. Br1-anim.gif
Bricard octahedron with a rectangle as its equator. The axis of symmetry passes perpendicularly through the center of the rectangle.
Bricard octahedron with an antiparallelogram as its equator. The axis of symmetry passes through the plane of the antiparallelogram. Br2-anim.gif
Bricard octahedron with an antiparallelogram as its equator. The axis of symmetry passes through the plane of the antiparallelogram.

In geometry, a Bricard octahedron is a member of a family of flexible polyhedra constructed by Raoul Bricard in 1897. [1] The overall shape of one of these polyhedron may change in a continuous motion, without any changes to the lengths of its edges nor to the shapes of its faces. [2] These octahedra were the first flexible polyhedra to be discovered. [3]

Contents

The Bricard octahedra have six vertices, twelve edges, and eight triangular faces, connected in the same way as a regular octahedron. Unlike the regular octahedron, the Bricard octahedra are all non-convex self-crossing polyhedra. By Cauchy's rigidity theorem, a flexible polyhedron must be non-convex, [3] but there exist other flexible polyhedra without self-crossings. Avoiding self-crossings requires more vertices (at least nine) than the six vertices of the Bricard octahedra. [4]

In his publication describing these octahedra, Bricard completely classified the flexible octahedra. His work in this area was later the subject of lectures by Henri Lebesgue at the Collège de France. [5]

Construction

A Bricard octahedron may be formed from three pairs of points, each symmetric around a common axis of 180° rotational symmetry, with no plane containing all six points. These points form the vertices of the octahedron. The triangular faces of the octahedron have one point from each of the three symmetric pairs. For each pair, there are two ways of choosing one point from the pair, so there are eight triangular faces altogether. The edges of the octahedron are the sides of these triangles, and include one point from each of two symmetric pairs. There are 12 edges, which form the octahedral graph K2,2,2. [2] [6]

As an example, the six points (0,0,±1), (0,±1,0), and (±1,0,0) form the vertices of a regular octahedron, with each point opposite in the octahedron to its negation, but this is not flexible. Instead, these same six points can be paired up differently to form a Bricard octahedron, with a diagonal axis of symmetry. If this axis is chosen as the line through the origin and the point (0,1,1), then the three symmetric pairs of points for this axis are (0,0,1)—(0,1,0), (0,0,−1)—(0,−1,0), and (1,0,0)–(−1,0,0). The resulting Bricard octahedron resembles one of the extreme configurations of the second animation, which has an equatorial antiparallelogram.

As a linkage

It is also possible to think of the Bricard octahedron as a mechanical linkage consisting of the twelve edges, connected by flexible joints at the vertices, without the faces. Omitting the faces eliminates the self-crossings for many (but not all) positions of these octahedra. The resulting kinematic chain has one degree of freedom of motion, the same as the polyhedron from which it is derived. [7]

Explanation

The quadrilaterals formed by the edges between the points in any two symmetric pairs of points can be thought of as equators of the octahedron. These equators have the property (by their symmetry) that opposite pairs of quadrilateral sides have equal length. Every quadrilateral with opposite pairs of equal sides, embedded in Euclidean space, has axial symmetry, and some (such as the rectangle) have other symmetries besides. If one cuts the Bricard octahedron into two open-bottomed pyramids by slicing it along one of its equators, both of these open pyramids can flex, and the flexing motion can be made to preserve the axis of symmetry of the whole shape. But, by the symmetries of its construction, the flexing motions of these two open pyramids both move the equator along which they were cut in the same way. Therefore, they can be glued back together into a single flexing motion of the whole octahedron. [2] [6]

The property of having opposite sides of equal length is true of the rectangle, parallelogram, and antiparallelogram, and it is possible to construct Bricard octahedra having any of those flat shapes as their equators. However, the equator of a Bricard octahedron is not required to lie in a plane; instead, it can be a skew quadrilateral. Even for Bricard octahedra constructed to have a flat equator, the equator generally does not remain flat as the octahedron flexes. [2] However, for some Bricard octahedra, such as the octahedron with an antiparallelogram equator shown in the illustration, the symmetries of the polyhedron cause its equator to remain planar at all times.

Additional properties

The Dehn invariant of any Bricard octahedron remains constant as it undergoes its flexing motion. [8] This same property has been proven for all non-self-crossing flexible polyhedra. [9] However, there exist other self-crossing flexible polyhedra for which the Dehn invariant changes continuously as they flex. [10]

Extensions

It is possible to modify the Bricard polyhedra by adding more faces, in order to move the self-crossing parts of the polyhedron away from each other while still allowing it to flex. The simplest of these modifications is Steffen's polyhedron, discovered by Klaus Steffen, with nine vertices and 14 triangular faces. [2] However, although it has been claimed to be the simplest possible flexible polyhedron without self-crossings, [4] a 2024 preprint by Gallet et al. claims to construct a simpler non-self-crossing flexible polyhedron with only eight vertices. Their polyhedron is obtained by combining two Bricard octahedra to form a self-crossing flexible pentagonal bipyramid, and then replacing one of its faces by three triangles to eliminate the self-crossing. [11]

By connecting together multiple shapes derived from the Bricard octahedron, it is possible to construct horn-shaped rigid origami forms whose shape traces out complicated space curves. [12]

Related Research Articles

In geometry, a bipyramid, dipyramid, or double pyramid is a polyhedron formed by fusing two pyramids together base-to-base. The polygonal base of each pyramid must therefore be the same, and unless otherwise specified the base vertices are usually coplanar and a bipyramid is usually symmetric, meaning the two pyramids are mirror images across their common base plane. When each apex of the bipyramid is on a line perpendicular to the base and passing through its center, it is a right bipyramid; otherwise it is oblique. When the base is a regular polygon, the bipyramid is also called regular.

<span class="mw-page-title-main">Cuboctahedron</span> Polyhedron with 8 triangular faces and 6 square faces

A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e., an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral. Its dual polyhedron is the rhombic dodecahedron.

In geometry, an octahedron is a polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Regular octahedra occur in nature as crystal structures. Many types of irregular octahedra also exist, including both convex and non-convex shapes.

<span class="mw-page-title-main">Polyhedron</span> 3D shape with flat faces, straight edges and sharp corners

In geometry, a polyhedron is a three-dimensional figure with flat polygonal faces, straight edges and sharp corners or vertices.

In geometry, a polyhedral compound is a figure that is composed of several polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram.

In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent regular polygons, and the same number of faces meet at each vertex. There are only five such polyhedra:

<span class="mw-page-title-main">Kite (geometry)</span> Quadrilateral symmetric across a diagonal

In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.

<span class="mw-page-title-main">Truncated octahedron</span> Archimedean solid

In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces, 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a 6-zonohedron. It is also the Goldberg polyhedron GIV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate 3-dimensional space, as a permutohedron.

In geometry, the Dehn invariant is a value used to determine whether one polyhedron can be cut into pieces and reassembled ("dissected") into another, and whether a polyhedron or its dissections can tile space. It is named after Max Dehn, who used it to solve Hilbert's third problem by proving that certain polyhedra with equal volume cannot be dissected into each other.

<span class="mw-page-title-main">Trapezohedron</span> Polyhedron made of congruent kites arranged radially

In geometry, an n-gonaltrapezohedron, n-trapezohedron, n-antidipyramid, n-antibipyramid, or n-deltohedron, is the dual polyhedron of an n-gonal antiprism. The 2n faces of an n-trapezohedron are congruent and symmetrically staggered; they are called twisted kites. With a higher symmetry, its 2n faces are kites.

<span class="mw-page-title-main">Tetrakis hexahedron</span> Catalan solid with 24 faces

In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid.

<span class="mw-page-title-main">Antiparallelogram</span> Polygon with four crossed edges of two lengths

In geometry, an antiparallelogram is a type of self-crossing quadrilateral. Like a parallelogram, an antiparallelogram has two opposite pairs of equal-length sides, but these pairs of sides are not in general parallel. Instead, each pair of sides is antiparallel with respect to the other, with sides in the longer pair crossing each other as in a scissors mechanism. Whereas a parallelogram's opposite angles are equal and oriented the same way, an antiparallelogram's are equal but oppositely oriented. Antiparallelograms are also called contraparallelograms or crossed parallelograms.

Cauchy's theorem is a theorem in geometry, named after Augustin Cauchy. It states that convex polytopes in three dimensions with congruent corresponding faces must be congruent to each other. That is, any polyhedral net formed by unfolding the faces of the polyhedron onto a flat surface, together with gluing instructions describing which faces should be connected to each other, uniquely determines the shape of the original polyhedron. For instance, if six squares are connected in the pattern of a cube, then they must form a cube: there is no convex polyhedron with six square faces connected in the same way that does not have the same shape.

<span class="mw-page-title-main">Flexible polyhedron</span>

In geometry, a flexible polyhedron is a polyhedral surface without any boundary edges, whose shape can be continuously changed while keeping the shapes of all of its faces unchanged. The Cauchy rigidity theorem shows that in dimension 3 such a polyhedron cannot be convex.

<span class="mw-page-title-main">Schönhardt polyhedron</span> Non-convex polyhedron with no triangulation

In geometry, a Schönhardt polyhedron is a polyhedron with the same combinatorial structure as a regular octahedron, but with dihedral angles that are non-convex along three disjoint edges. Because it has no interior diagonals, it cannot be triangulated into tetrahedra without adding new vertices. It has the fewest vertices of any polyhedron that cannot be triangulated. It is named after the German mathematician Erich Schönhardt, who described it in 1928, although the artist Karlis Johansons had exhibited a related structure in 1921.

<span class="mw-page-title-main">Jessen's icosahedron</span> Right-angled non-convex polyhedron

Jessen's icosahedron, sometimes called Jessen's orthogonal icosahedron, is a non-convex polyhedron with the same numbers of vertices, edges, and faces as the regular icosahedron. It is named for Børge Jessen, who studied it in 1967. In 1971, a family of nonconvex polyhedra including this shape was independently discovered and studied by Adrien Douady under the name six-beakedshaddock; later authors have applied variants of this name more specifically to Jessen's icosahedron.

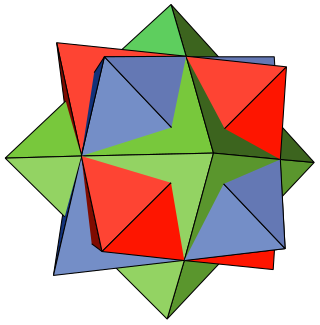
<span class="mw-page-title-main">Compound of three octahedra</span> Polyhedral compound

In mathematics, the compound of three octahedra or octahedron 3-compound is a polyhedral compound formed from three regular octahedra, all sharing a common center but rotated with respect to each other. Although appearing earlier in the mathematical literature, it was rediscovered and popularized by M. C. Escher, who used it in the central image of his 1948 woodcut Stars.

<span class="mw-page-title-main">First stellation of the rhombic dodecahedron</span> Self I intersecting polyhedron with 12 faces

In geometry, the first stellation of the rhombic dodecahedron is a self-intersecting polyhedron with 12 faces, each of which is a non-convex hexagon. It is a stellation of the rhombic dodecahedron and has the same outer shell and the same visual appearance as two other shapes: a solid, Escher's solid, with 48 triangular faces, and a polyhedral compound of three flattened octahedra with 24 overlapping triangular faces.

<span class="mw-page-title-main">Steffen's polyhedron</span> Flexible polyhedron with 14 triangle faces

In geometry, Steffen's polyhedron is a flexible polyhedron discovered by and named after Klaus Steffen. It is based on the Bricard octahedron, but unlike the Bricard octahedron its surface does not cross itself. It has nine vertices, 21 edges, and 14 triangular faces. Its faces can be decomposed into three subsets: two six-triangle-patches from a Bricard octahedron, and two more triangles that link these patches together.

<span class="mw-page-title-main">Kinematics of the cuboctahedron</span> Symmetrical transformations of the cuboctahedron into related uniform polyhedra

The skeleton of a cuboctahedron, considering its edges as rigid beams connected at flexible joints at its vertices but omitting its faces, does not have structural rigidity. Consequently, its vertices can be repositioned by folding at the edges and face diagonals. The cuboctahedron's kinematics is noteworthy in that its vertices can be repositioned to the vertex positions of the regular icosahedron, the Jessen's icosahedron, and the regular octahedron, in accordance with the pyritohedral symmetry of the icosahedron.

References

  1. ↑ Bricard, Raoul (1897), "Mémoire sur la théorie de l'octaèdre articulé", Journal de mathématiques pures et appliquées, 5e série (in French), 3: 113–150. Translated as "Memoir on the Theory of the Articulated Octahedron" by E. A. Coutsias, 2010.
  2. 1 2 3 4 5 Connelly, Robert (1981), "Flexing surfaces", in Klarner, David A. (ed.), The Mathematical Gardner, Springer, pp. 79–89, doi:10.1007/978-1-4684-6686-7_10, ISBN   978-1-4684-6688-1 .
  3. 1 2 Stewart, Ian (2004), Math Hysteria: Fun and games with mathematics, Oxford: Oxford University Press, p. 116, ISBN   9780191647451 .
  4. 1 2 Demaine, Erik D.; O'Rourke, Joseph (2007), "23.2 Flexible polyhedra", Geometric Folding Algorithms: Linkages, origami, polyhedra, Cambridge University Press, Cambridge, pp. 345–348, doi:10.1017/CBO9780511735172, ISBN   978-0-521-85757-4, MR   2354878 .
  5. ↑ Lebesgue H., "Octaedres articules de Bricard", Enseign. Math., Series 2 (in French), 13 (3): 175–185, doi:10.5169/seals-41541
  6. 1 2 Fuchs, Dmitry; Tabachnikov, Serge (2007), Mathematical Omnibus: Thirty lectures on classic mathematics, Providence, RI: American Mathematical Society, p. 347, doi:10.1090/mbk/046, ISBN   978-0-8218-4316-1, MR   2350979 .
  7. ↑ Cromwell, Peter R. (1997), Polyhedra, Cambridge: Cambridge University Press, p. 239, ISBN   0-521-55432-2, MR   1458063 .
  8. ↑ Alexandrov, Victor (2010), "The Dehn invariants of the Bricard octahedra", Journal of Geometry, 99 (1–2): 1–13, arXiv: 0901.2989 , doi:10.1007/s00022-011-0061-7, MR   2823098 .
  9. ↑ Gaĭfullin, A. A.; Ignashchenko, L. S. (2018), "Dehn invariant and scissors congruence of flexible polyhedra", Trudy Matematicheskogo Instituta Imeni V. A. Steklova, 302 (Topologiya i Fizika): 143–160, doi:10.1134/S0371968518030068, ISBN   5-7846-0147-4, MR   3894642
  10. ↑ Alexandrov, Victor; Connelly, Robert (2011), "Flexible suspensions with a hexagonal equator", Illinois Journal of Mathematics, 55 (1): 127–155, arXiv: 0905.3683 , doi:10.1215/ijm/1355927031, MR   3006683 .
  11. ↑ Gallet, Matteo; Grasegger, Georg; Legerský, Jan; Schicho, Josef (October 17, 2024), Pentagonal bipyramids lead to the smallest flexible embedded polyhedron, arXiv: 2410.13811
  12. ↑ Tachi, Tomohiro (2016), "Designing rigidly foldable horns using Bricard's octahedron", Journal of Mechanisms and Robotics, 8 (3): 031008, doi:10.1115/1.4031717 .
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.