
A quasiperiodic crystal, or quasicrystal, is a structure that is ordered but not periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks translational symmetry. While crystals, according to the classical crystallographic restriction theorem, can possess only two-, three-, four-, and six-fold rotational symmetries, the Bragg diffraction pattern of quasicrystals shows sharp peaks with other symmetry orders—for instance, five-fold.

Origami is the Japanese art of paper folding. In modern usage, the word "origami" is often used as an inclusive term for all folding practices, regardless of their culture of origin. The goal is to transform a flat square sheet of paper into a finished sculpture through folding and sculpting techniques. Modern origami practitioners generally discourage the use of cuts, glue, or markings on the paper. Origami folders often use the Japanese word kirigami to refer to designs which use cuts.

The discipline of origami or paper folding has received a considerable amount of mathematical study. Fields of interest include a given paper model's flat-foldability, and the use of paper folds to solve up-to cubic mathematical equations.

A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries.
A gravastar is an object hypothesized in astrophysics by Pawel O. Mazur and Emil Mottola as an alternative to the black hole theory. It has usual black hole metric outside of the horizon, but de Sitter metric inside. On the horizon there is a thin shell of matter. The term "gravastar" is a portmanteau of the words "gravitational vacuum star". Further theoretical considerations of gravastars include the notion of a nestar.

In botany, phyllotaxis or phyllotaxy is the arrangement of leaves on a plant stem. Phyllotactic spirals form a distinctive class of patterns in nature.
The Little–Parks effect was discovered in 1962 by William A. Little and Ronald D. Parks in experiments with empty and thin-walled superconducting cylinders subjected to a parallel magnetic field. It was one of the first experiments to indicate the importance of Cooper-pairing principle in BCS theory.

In geometry, the rhombille tiling, also known as tumbling blocks, reversible cubes, or the dice lattice, is a tessellation of identical 60° rhombi on the Euclidean plane. Each rhombus has two 60° and two 120° angles; rhombi with this shape are sometimes also called diamonds. Sets of three rhombi meet at their 120° angles, and sets of six rhombi meet at their 60° angles.
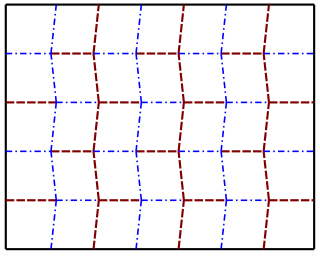
The Miura fold is a method of folding a flat surface such as a sheet of paper into a smaller area. The fold is named for its inventor, Japanese astrophysicist Kōryō Miura.
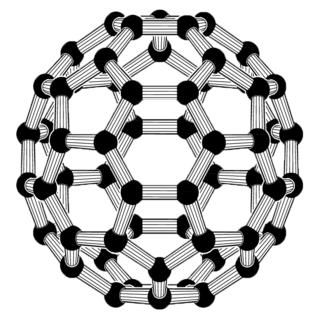
The mechanical properties of carbon nanotubes reveal them as one of the strongest materials in nature. Carbon nanotubes (CNTs) are long hollow cylinders of graphene. Although graphene sheets have 2D symmetry, carbon nanotubes by geometry have different properties in axial and radial directions. It has been shown that CNTs are very strong in the axial direction. Young's modulus on the order of 270 - 950 GPa and tensile strength of 11 - 63 GPa were obtained.

Silicene is a two-dimensional allotrope of silicon, with a hexagonal honeycomb structure similar to that of graphene. Contrary to graphene, silicene is not flat, but has a periodically buckled topology; the coupling between layers in silicene is much stronger than in multilayered graphene; and the oxidized form of silicene, 2D silica, has a very different chemical structure from graphene oxide.
Twisted geometries are discrete geometries that play a role in loop quantum gravity and spin foam models, where they appear in the semiclassical limit of spin networks. A twisted geometry can be visualized as collections of polyhedra dual to the nodes of the spin network's graph. Intrinsic and extrinsic curvatures are defined in a manner similar to Regge calculus, but with the generalisation of including a certain type of metric discontinuities: the face shared by two adjacent polyhedra has a unique area, but its shape can be different. This is a consequence of the quantum geometry of spin networks: ordinary Regge calculus is "too rigid" to account for all the geometric degrees of freedom described by the semiclassical limit of a spin network.

Magnetized liner inertial fusion (MagLIF) is an ongoing fusion power experiment being carried out on the Z Pulsed Power Facility at Sandia National Laboratories in the US. Is it one example of the broader magneto-inertial fusion approach, which attempts to compress a pre-heated plasma. The goal is to produce fusion conditions without the level of compression needed in the inertial confinement fusion (ICF) approach, where the required densities reach about 100 times that of lead.
Mechanical metamaterials are artificial materials with mechanical properties that are defined by their mesostructure in addition to than their composition. They can be seen as a counterpart to the rather well-known family of optical metamaterials. They are often also termed elastodynamic metamaterials and include acoustic metamaterials as a special case of vanishing shear. Their mechanical properties can be designed to have values which cannot be found in nature.

In astrophysics and nuclear physics, nuclear pasta is a theoretical type of degenerate matter that is postulated to exist within the crusts of neutron stars. If it exists, nuclear pasta would be the strongest material in the universe. Between the surface of a neutron star and the quark–gluon plasma at the core, at matter densities of 1014 g/cm3, nuclear attraction and Coulomb repulsion forces are of comparable magnitude. The competition between the forces leads to the formation of a variety of complex structures assembled from neutrons and protons. Astrophysicists call these types of structures nuclear pasta because the geometry of the structures resembles various types of pasta.

This is a bibliography of works by Theodore von Kármán.

In mathematics, the Schwarz lantern is a polyhedral approximation to a cylinder, used as a pathological example of the difficulty of defining the area of a smooth (curved) surface as the limit of the areas of polyhedra. It is formed by stacked rings of isosceles triangles, arranged within each ring in the same pattern as an antiprism. The resulting shape can be folded from paper, and is named after mathematician Hermann Schwarz and for its resemblance to a cylindrical paper lantern. It is also known as Schwarz's boot, Schwarz's polyhedron, or the Chinese lantern.
The rotating wall technique is a method used to compress a single-component plasma confined in an electromagnetic trap. It is one of many scientific and technological applications that rely on storing charged particles in vacuum. This technique has found extensive use in improving the quality of these traps and in tailoring of both positron and antiproton plasmas for a variety of end uses.
Tomohiro Tachi is a Japanese academic who studies origami from an interdisciplinary perspective, combining approaches from the mathematics of paper folding, structural rigidity, computational geometry, architecture, and materials science. His work was profiled in "The Origami Revolution" (2017), part of the Nova series of US science documentaries. He is a professor at the University of Tokyo.
John Pascal Vinti was an American theoretical physicist, who published papers not only in physics, but also in mathematics and engineering. He is known for the Vinti integral.














