Related Research Articles

In statistics, cluster sampling is a sampling plan used when mutually homogeneous yet internally heterogeneous groupings are evident in a statistical population. It is often used in marketing research. In this sampling plan, the total population is divided into these groups and a simple random sample of the groups is selected. The elements in each cluster are then sampled. If all elements in each sampled cluster are sampled, then this is referred to as a "one-stage" cluster sampling plan. If a simple random subsample of elements is selected within each of these groups, this is referred to as a "two-stage" cluster sampling plan. A common motivation for cluster sampling is to reduce the total number of interviews and costs given the desired accuracy. For a fixed sample size, the expected random error is smaller when most of the variation in the population is present internally within the groups, and not between the groups.
In statistics, survey sampling describes the process of selecting a sample of elements from a target population to conduct a survey. The term "survey" may refer to many different types or techniques of observation. In survey sampling it most often involves a questionnaire used to measure the characteristics and/or attitudes of people. Different ways of contacting members of a sample once they have been selected is the subject of survey data collection. The purpose of sampling is to reduce the cost and/or the amount of work that it would take to survey the entire target population. A survey that measures the entire target population is called a census. A sample refers to a group or section of a population from which information is to be obtained
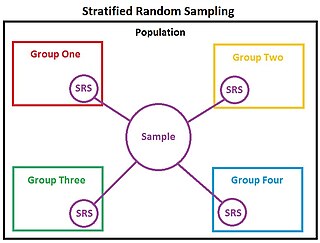
In statistics, stratified sampling is a method of sampling from a population which can be partitioned into subpopulations.

An experiment is a procedure carried out to support or refute a hypothesis. Experiments provide insight into cause-and-effect by demonstrating what outcome occurs when a particular factor is manipulated. Experiments vary greatly in goal and scale, but always rely on repeatable procedure and logical analysis of the results. There also exist natural experimental studies.
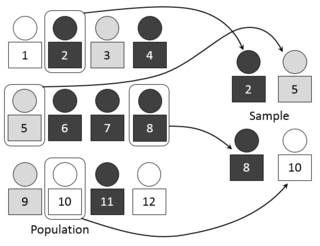
In statistics, quality assurance, and survey methodology, sampling is the selection of a subset of individuals from within a statistical population to estimate characteristics of the whole population. Statisticians attempt for the samples to represent the population in question. Two advantages of sampling are lower cost and faster data collection than measuring the entire population.
Stratification may refer to:
Survey methodology is "the study of survey methods". As a field of applied statistics concentrating on human-research surveys, survey methodology studies the sampling of individual units from a population and associated techniques of survey data collection, such as questionnaire construction and methods for improving the number and accuracy of responses to surveys. Survey methodology targets instruments or procedures that ask one or more questions that may or may not be answered.
A cohort study is a particular form of longitudinal study that samples a cohort, performing a cross-section at intervals through time. It is a type of panel study where the individuals in the panel share a common characteristic.
Quota sampling is a method for selecting survey participants that is a non-probabilistic version of stratified sampling.

A scientific control is an experiment or observation designed to minimize the effects of variables other than the independent variable. This increases the reliability of the results, often through a comparison between control measurements and the other measurements. Scientific controls are a part of the scientific method.
Sample size determination is the act of choosing the number of observations or replicates to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a population from a sample. In practice, the sample size used in a study is usually determined based on the cost, time, or convenience of collecting the data, and the need for it to offer sufficient statistical power. In complicated studies there may be several different sample sizes: for example, in a stratified survey there would be different sizes for each stratum. In a census, data is sought for an entire population, hence the intended sample size is equal to the population. In experimental design, where a study may be divided into different treatment groups, there may be different sample sizes for each group.
Random assignment or random placement is an experimental technique for assigning human participants or animal subjects to different groups in an experiment using randomization, such as by a chance procedure or a random number generator. This ensures that each participant or subject has an equal chance of being placed in any group. Random assignment of participants helps to ensure that any differences between and within the groups are not systematic at the outset of the experiment. Thus, any differences between groups recorded at the end of the experiment can be more confidently attributed to the experimental procedures or treatment.
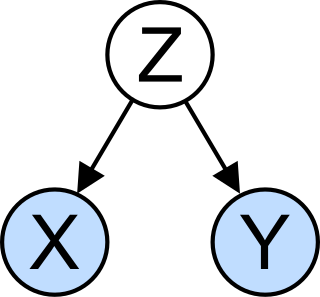
In statistics, a confounder is a variable that influences both the dependent variable and independent variable, causing a spurious association. Confounding is a causal concept, and as such, cannot be described in terms of correlations or associations.

A quasi-experiment is an empirical interventional study used to estimate the causal impact of an intervention on target population without random assignment. Quasi-experimental research shares similarities with the traditional experimental design or randomized controlled trial, but it specifically lacks the element of random assignment to treatment or control. Instead, quasi-experimental designs typically allow the researcher to control the assignment to the treatment condition, but using some criterion other than random assignment.
In the statistical analysis of observational data, propensity score matching (PSM) is a statistical matching technique that attempts to estimate the effect of a treatment, policy, or other intervention by accounting for the covariates that predict receiving the treatment. PSM attempts to reduce the bias due to confounding variables that could be found in an estimate of the treatment effect obtained from simply comparing outcomes among units that received the treatment versus those that did not. Paul R. Rosenbaum and Donald Rubin introduced the technique in 1983.
Balanced repeated replication is a statistical technique for estimating the sampling variability of a statistic obtained by stratified sampling.
In survey methodology, the design effect is the ratio between the variances of two estimators to some parameter of interest. Specifically the ratio of an actual variance of an estimator that is based on a sample from some sampling design, to the variance of an alternative estimator that would be calculated (hypothetically) using a sample from a simple random sample (SRS) of the same number of elements. It measures the expected effect of the design structure on the variance of some estimator of interest. The design effect is a positive real number that can indicate an inflation, or deflation in the variance of an estimator for some parameter, that is due to the study not using SRS.
Principal stratification is a statistical technique used in causal inference when adjusting results for post-treatment covariates. The idea is to identify underlying strata and then compute causal effects only within strata. It is a generalization of the local average treatment effect (LATE).
In statistics, the Cochran–Mantel–Haenszel test (CMH) is a test used in the analysis of stratified or matched categorical data. It allows an investigator to test the association between a binary predictor or treatment and a binary outcome such as case or control status while taking into account the stratification. Unlike the McNemar test which can only handle pairs, the CMH test handles arbitrary strata size. It is named after William G. Cochran, Nathan Mantel and William Haenszel. Extensions of this test to a categorical response and/or to several groups are commonly called Cochran–Mantel–Haenszel statistics. It is often used in observational studies where random assignment of subjects to different treatments cannot be controlled, but confounding covariates can be measured.

In statistics, stratified randomization is a method of sampling which first stratifies the whole study population into subgroups with same attributes or characteristics, known as strata, then followed by simple random sampling from the stratified groups, where each element within the same subgroup are selected unbiasedly during any stage of the sampling process, randomly and entirely by chance. Stratified randomization is considered a subdivision of stratified sampling, and should be adopted when shared attributes exist partially and vary widely between subgroups of the investigated population, so that they require special considerations or clear distinctions during sampling. This sampling method should be distinguished from cluster sampling, where a simple random sample of several entire clusters is selected to represent the whole population, or stratified systematic sampling, where a systematic sampling is carried out after the stratification process. Stratified random sampling is sometimes also known as "quota random sampling".