Superformula

This article is about a generalization of the superellipse. For the Japanese formula racing series, see Super Formula Championship.

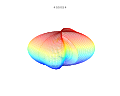
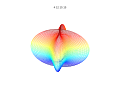
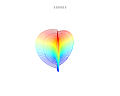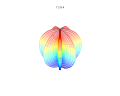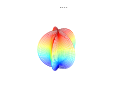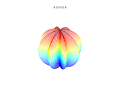The superformula is a generalization of the superellipse and was proposed by Johan Gielis in 2003. ^[1] Gielis suggested that the formula can be used to describe many complex shapes and curves that are found in nature. Gielis has filed a patent application related to the synthesis of patterns generated by the superformula, which expired effective 2020-05-10. ^[2]

In polar coordinates, with ${\displaystyle r}$ the radius and ${\displaystyle \varphi }$ the angle, the superformula is:

$${\displaystyle r\left(\varphi \right)=\left(\left|{\frac {\cos \left({\frac {m\varphi }{4}}\right)}{a}}\right|^{n_{2}}+\left|{\frac {\sin \left({\frac {m\varphi }{4}}\right)}{b}}\right|^{n_{3}}\right)^{-{\frac {1}{n_{1}}}}.}$$ By choosing different values for the parameters ${\displaystyle a,b,m,n_{1},n_{2},}$ and ${\displaystyle n_{3},}$ different shapes can be generated.

The formula was obtained by generalizing the superellipse, named and popularized by Piet Hein, a Danish mathematician.

2D plots

In the following examples the values shown above each figure should be m, n₁, n₂ and n₃.

A GNU Octave program for generating these figures

functionsf2d(n, a)u=[0:.001:2*pi];raux=abs(1/a(1).*abs(cos(n(1)*u/4))).^n(3)+abs(1/a(2).*abs(sin(n(1)*u/4))).^n(4);r=abs(raux).^(-1/n(2));x=r.*cos(u);y=r.*sin(u);plot(x,y);end

Extension to higher dimensions

It is possible to extend the formula to 3, 4, or n dimensions, by means of the spherical product of superformulas. For example, the 3D parametric surface is obtained by multiplying two superformulas r₁ and r₂. The coordinates are defined by the relations:

$${\displaystyle x=r_{1}(\theta )\cos \theta \cdot r_{2}(\phi )\cos \phi ,}$$$${\displaystyle y=r_{1}(\theta )\sin \theta \cdot r_{2}(\phi )\cos \phi ,}$$$${\displaystyle z=r_{2}(\phi )\sin \phi ,}$$

where ${\displaystyle \phi }$ (latitude) varies between −π/2 and π/2 and θ (longitude) between −π and π.

3D plots

3D superformula: a = b = 1; m, n₁, n₂ and n₃ are shown in the pictures.

• 
• 
• 
• 
• 
• 
• 
• 

A GNU Octave program for generating these figures:

functionsf3d(n, a)u=[-pi:.05:pi];v=[-pi/2:.05:pi/2];nu=length(u);nv=length(v);fori=1:nuforj=1:nvraux1=abs(1/a(1)*abs(cos(n(1).*u(i)/4))).^n(3)+abs(1/a(2)*abs(sin(n(1)*u(i)/4))).^n(4);r1=abs(raux1).^(-1/n(2));raux2=abs(1/a(1)*abs(cos(n(1)*v(j)/4))).^n(3)+abs(1/a(2)*abs(sin(n(1)*v(j)/4))).^n(4);r2=abs(raux2).^(-1/n(2));x(i,j)=r1*cos(u(i))*r2*cos(v(j));y(i,j)=r1*sin(u(i))*r2*cos(v(j));z(i,j)=r2*sin(v(j));endfor;endfor;mesh(x,y,z);endfunction;

Generalization

The superformula can be generalized by allowing distinct m parameters in the two terms of the superformula. By replacing the first parameter ${\displaystyle m}$ with y and second parameter ${\displaystyle m}$ with z: ^[3] $${\displaystyle r\left(\varphi \right)=\left(\left|{\frac {\cos \left({\frac {y\varphi }{4}}\right)}{a}}\right|^{n_{2}}+\left|{\frac {\sin \left({\frac {z\varphi }{4}}\right)}{b}}\right|^{n_{3}}\right)^{-{\frac {1}{n_{1}}}}}$$

This allows the creation of rotationally asymmetric and nested structures. In the following examples a, b, ${\displaystyle {n_{2}}}$ and ${\displaystyle {n_{3}}}$ are 1:

References

1. Gielis, Johan (2003), "A generic geometric transformation that unifies a wide range of natural and abstract shapes" , American Journal of Botany , 90 (3): 333–338, doi:10.3732/ajb.90.3.333, ISSN   0002-9122, PMID   21659124
2. EPpatent 1177529,Gielis, Johan,"Method and apparatus for synthesizing patterns",issued 2005-02-02 
3. • Stöhr, Uwe (2004), SuperformulaU (PDF), archived from the original (PDF) on December 8, 2017

External links

• Some Experiments on Fitting of Gielis Curves by Simulated Annealing and Particle Swarm Methods of Global Optimization
• Least Squares Fitting of Chacón-Gielis Curves By the Particle Swarm Method of Optimization
• Superformula 2D Plotter & SVG Generator
• Interactive example using JSXGraph
• SuperShaper: An OpenSource, OpenCL accelerated, interactive 3D SuperShape generator with shader based visualisation (OpenGL3)