Continuum mechanics is a branch of mechanics that deals with the deformation of and transmission of forces through materials modeled as a continuous medium rather than as discrete particles. The French mathematician Augustin-Louis Cauchy was the first to formulate such models in the 19th century.
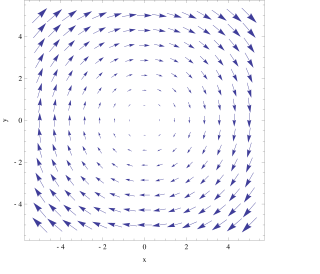
In vector calculus, the curl, also known as rotor, is a vector operator that describes the infinitesimal circulation of a vector field in three-dimensional Euclidean space. The curl at a point in the field is represented by a vector whose length and direction denote the magnitude and axis of the maximum circulation. The curl of a field is formally defined as the circulation density at each point of the field.
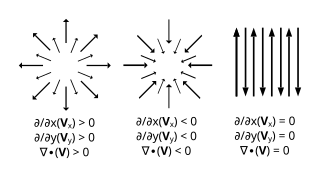
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the quantity of the vector field's source at each point. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around a given point.

In vector calculus, the gradient of a scalar-valued differentiable function of several variables is the vector field whose value at a point is the "direction and rate of fastest increase". The gradient transforms like a vector under change of basis of the space of variables of . If the gradient of a function is non-zero at a point , the direction of the gradient is the direction in which the function increases most quickly from , and the magnitude of the gradient is the rate of increase in that direction, the greatest absolute directional derivative. Further, a point where the gradient is the zero vector is known as a stationary point. The gradient thus plays a fundamental role in optimization theory, where it is used to maximize a function by gradient ascent. In coordinate-free terms, the gradient of a function may be defined by:
In quantum mechanics, the Hamiltonian of a system is an operator corresponding to the total energy of that system, including both kinetic energy and potential energy. Its spectrum, the system's energy spectrum or its set of energy eigenvalues, is the set of possible outcomes obtainable from a measurement of the system's total energy. Due to its close relation to the energy spectrum and time-evolution of a system, it is of fundamental importance in most formulations of quantum theory.
Flux describes any effect that appears to pass or travel through a surface or substance. Flux is a concept in applied mathematics and vector calculus which has many applications to physics. For transport phenomena, flux is a vector quantity, describing the magnitude and direction of the flow of a substance or property. In vector calculus flux is a scalar quantity, defined as the surface integral of the perpendicular component of a vector field over a surface.

The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances, named after French engineer and physicist Claude-Louis Navier and Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).
In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, is a theorem which relates the flux of a vector field through a closed surface to the divergence of the field in the volume enclosed.

In geometry, a normal is an object that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the (infinite) line perpendicular to the tangent line to the curve at the point. A normal vector may have length one or its length may represent the curvature of the object. Multiplying a normal vector by -1 results in the opposite vector, which may be used for indicating sides.
In continuum mechanics, the infinitesimal strain theory is a mathematical approach to the description of the deformation of a solid body in which the displacements of the material particles are assumed to be much smaller than any relevant dimension of the body; so that its geometry and the constitutive properties of the material at each point of space can be assumed to be unchanged by the deformation.
A Newtonian fluid is a fluid in which the viscous stresses arising from its flow are at every point linearly correlated to the local strain rate — the rate of change of its deformation over time. Stresses are proportional to the rate of change of the fluid's velocity vector.

In mathematical physics, scalar potential, simply stated, describes the situation where the difference in the potential energies of an object in two different positions depends only on the positions, not upon the path taken by the object in traveling from one position to the other. It is a scalar field in three-space: a directionless value (scalar) that depends only on its location. A familiar example is potential energy due to gravity.
A directional derivative is a concept in multivariable calculus that measures the rate at which a function changes in a particular direction at a given point.
In mathematics, the Neumannboundary condition is a type of boundary condition, named after Carl Neumann. When imposed on an ordinary or a partial differential equation, the condition specifies the values of the derivative applied at the boundary of the domain.
In mathematics, Green's identities are a set of three identities in vector calculus relating the bulk with the boundary of a region on which differential operators act. They are named after the mathematician George Green, who discovered Green's theorem.
In differential geometry, the four-gradient is the four-vector analogue of the gradient from vector calculus.
In physics and engineering, mass flux is the rate of mass flow. Its SI units are kg m−2 s−1. The common symbols are j, J, q, Q, φ, or Φ, sometimes with subscript m to indicate mass is the flowing quantity. Mass flux can also refer to an alternate form of flux in Fick's law that includes the molecular mass, or in Darcy's law that includes the mass density.
In fluid mechanics and mathematics, a capillary surface is a surface that represents the interface between two different fluids. As a consequence of being a surface, a capillary surface has no thickness in slight contrast with most real fluid interfaces.
Kirchhoff's integral theorem is a surface integral to obtain the value of the solution of the homogeneous scalar wave equation at an arbitrary point P in terms of the values of the solution and the solution's first-order derivative at all points on an arbitrary closed surface that encloses P. It is derived by using the Green's second identity and the homogeneous scalar wave equation that makes the volume integration in the Green's second identity zero.

Gradient vector flow (GVF), a computer vision framework introduced by Chenyang Xu and Jerry L. Prince, is the vector field that is produced by a process that smooths and diffuses an input vector field. It is usually used to create a vector field from images that points to object edges from a distance. It is widely used in image analysis and computer vision applications for object tracking, shape recognition, segmentation, and edge detection. In particular, it is commonly used in conjunction with active contour model.










