Symmetry-adapted perturbation theory

Last updated July 18, 2023

Symmetry-adapted perturbation theory or SAPT^[1]^[2] is a methodology in electronic structure theory developed to describe non-covalent interactions between atoms and/or molecules. SAPT is a member of the family of methods known as energy decomposition analysis (EDA). Most EDA methods decompose a total interaction energy that is computed via a supermolecular approach, such that:

\Delta E_{\rm {int}}=E_{\rm {AB}}-E_{\rm {A}}-E_{\rm {B}}

where ${\textstyle \Delta E_{\rm {int}}}$ is the total interaction energy obtained via subtracting isolated monomer energies ${\textstyle E_{\rm {A}}}$ and $E_{\rm {B}}$ from the dimer energy ${\textstyle E_{\rm {AB}}}$ . A key deficiency of the supermolecular interaction energy is that it is susceptible to basis set superposition error (BSSE).

The major difference between SAPT and supermolecular EDA methods is that, as the name suggests, SAPT computes the interaction energy directly via a perturbative approach. One consequence of capturing the total interaction energy as a perturbation to the total system energy rather than using the subtractive supermolecular method outlined above, is that the interaction energy is made free of BSSE in a natural way.

Being a perturbation expansion, SAPT also provides insight into the contributing components to the interaction energy. The lowest-order expansion at which all interaction energy components are obtained is second-order in the intermolecular perturbation. The simplest such SAPT approach is called SAPT0 because it neglects intramolecular correlation effects (i.e., it is based on Hartree–Fock densities). SAPT0 captures the classical electrostatic interaction of two charge densities and exchange (or Pauli repulsion) at first-order, and at second-order the terms for electrostatic induction (the polarization of the molecular orbitals in the electric field of the interacting atom/molecule) and dispersion (see London dispersion) appear, along with their exchange counterparts.

E_{\rm {int}}^{\rm {SAPT0}}=E_{\rm {elst}}^{(1)}+E_{\rm {exch}}^{(1)}+E_{\rm {ind}}^{(2)}+E_{\text{exch-ind}}^{(2)}+E_{\rm {disp}}^{(2)}+E_{\text{exch-disp}}^{(2)}

Higher terms in the perturbation series can be accounted for using many-body perturbation theory or coupled-cluster approaches. Alternatively, density functional theory variants of SAPT have been formulated. The higher-level SAPT methods approach supermolecular coupled-cluster singles, doubles, and perturbative triples [CCSD(T)] in accuracy.^[3]

Related Research Articles

An intermolecular force (IMF) is the force that mediates interaction between molecules, including the electromagnetic forces of attraction or repulsion which act between atoms and other types of neighbouring particles, e.g. atoms or ions. Intermolecular forces are weak relative to intramolecular forces – the forces which hold a molecule together. For example, the covalent bond, involving sharing electron pairs between atoms, is much stronger than the forces present between neighboring molecules. Both sets of forces are essential parts of force fields frequently used in molecular mechanics.

In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines classical field theory, special relativity, and quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and in condensed matter physics to construct models of quasiparticles.

In mathematics and applied mathematics, perturbation theory comprises methods for finding an approximate solution to a problem, by starting from the exact solution of a related, simpler problem. A critical feature of the technique is a middle step that breaks the problem into "solvable" and "perturbative" parts. In perturbation theory, the solution is expressed as a power series in a small parameter $.$ The first term is the known solution to the solvable problem. Successive terms in the series at higher powers of $usually become smaller. An approximate 'perturbation solution' is obtained by truncating the series, usually by keeping only the first two terms, the solution to the known problem and the 'first order' perturbation correction.$

An instanton is a notion appearing in theoretical and mathematical physics. An instanton is a classical solution to equations of motion with a finite, non-zero action, either in quantum mechanics or in quantum field theory. More precisely, it is a solution to the equations of motion of the classical field theory on a Euclidean spacetime.

London dispersion forces are a type of intermolecular force acting between atoms and molecules that are normally electrically symmetric; that is, the electrons are symmetrically distributed with respect to the nucleus. They are part of the van der Waals forces. The LDF is named after the German physicist Fritz London. They are the weakest intermolecular force.

<span class="mw-page-title-main">Stark effect</span> Spectral line splitting in electrical field

The Stark effect is the shifting and splitting of spectral lines of atoms and molecules due to the presence of an external electric field. It is the electric-field analogue of the Zeeman effect, where a spectral line is split into several components due to the presence of the magnetic field. Although initially coined for the static case, it is also used in the wider context to describe the effect of time-dependent electric fields. In particular, the Stark effect is responsible for the pressure broadening of spectral lines by charged particles in plasmas. For most spectral lines, the Stark effect is either linear or quadratic with a high accuracy.

In mathematical physics, Yang–Mills theory is a gauge theory based on a special unitary group $SU(n)$ , or more generally any compact, reductive Lie algebra. Yang–Mills theory seeks to describe the behavior of elementary particles using these non-abelian Lie groups and is at the core of the unification of the electromagnetic force and weak forces (i.e. $U(1) \times SU(2)$ ) as well as quantum chromodynamics, the theory of the strong force (based on $SU(3)$ ). Thus it forms the basis of our understanding of the Standard Model of particle physics.

In physics, a coupling constant or gauge coupling parameter, is a number that determines the strength of the force exerted in an interaction. Originally, the coupling constant related the force acting between two static bodies to the "charges" of the bodies divided by the distance squared, $, between the bodies; thus: in for Newtonian gravity and in for electrostatic. This description remains valid in modern physics for linear theories with static bodies and massless force carriers.$

In physics, interaction energy is the contribution to the total energy that is caused by an interaction between the objects being considered.

Jellium, also known as the uniform electron gas (UEG) or homogeneous electron gas (HEG), is a quantum mechanical model of interacting electrons in a solid where the positive charges are assumed to be uniformly distributed in space; the electron density is a uniform quantity as well in space. This model allows one to focus on the effects in solids that occur due to the quantum nature of electrons and their mutual repulsive interactions without explicit introduction of the atomic lattice and structure making up a real material. Jellium is often used in solid-state physics as a simple model of delocalized electrons in a metal, where it can qualitatively reproduce features of real metals such as screening, plasmons, Wigner crystallization and Friedel oscillations.

In quantum physics, the spin–orbit interaction is a relativistic interaction of a particle's spin with its motion inside a potential. A key example of this phenomenon is the spin–orbit interaction leading to shifts in an electron's atomic energy levels, due to electromagnetic interaction between the electron's magnetic dipole, its orbital motion, and the electrostatic field of the positively charged nucleus. This phenomenon is detectable as a splitting of spectral lines, which can be thought of as a Zeeman effect product of two relativistic effects: the apparent magnetic field seen from the electron perspective and the magnetic moment of the electron associated with its intrinsic spin. A similar effect, due to the relationship between angular momentum and the strong nuclear force, occurs for protons and neutrons moving inside the nucleus, leading to a shift in their energy levels in the nucleus shell model. In the field of spintronics, spin–orbit effects for electrons in semiconductors and other materials are explored for technological applications. The spin–orbit interaction is at the origin of magnetocrystalline anisotropy and the spin Hall effect.

In theoretical physics, explicit symmetry breaking is the breaking of a symmetry of a theory by terms in its defining equations of motion that do not respect the symmetry. Usually this term is used in situations where these symmetry-breaking terms are small, so that the symmetry is approximately respected by the theory. An example is the spectral line splitting in the Zeeman effect, due to a magnetic interaction perturbation in the Hamiltonian of the atoms involved.

This article describes the mathematics of the Standard Model of particle physics, a gauge quantum field theory containing the internal symmetries of the unitary product group $SU(3) \times SU(2) \times U(1)$ . The theory is commonly viewed as describing the fundamental set of particles – the leptons, quarks, gauge bosons and the Higgs boson.

Electronic correlation is the interaction between electrons in the electronic structure of a quantum system. The correlation energy is a measure of how much the movement of one electron is influenced by the presence of all other electrons.

Chiral perturbation theory (ChPT) is an effective field theory constructed with a Lagrangian consistent with the (approximate) chiral symmetry of quantum chromodynamics (QCD), as well as the other symmetries of parity and charge conjugation. ChPT is a theory which allows one to study the low-energy dynamics of QCD on the basis of this underlying chiral symmetry.

In physics, a gauge theory is a type of field theory in which the Lagrangian does not change under local transformations according to certain smooth families of operations.

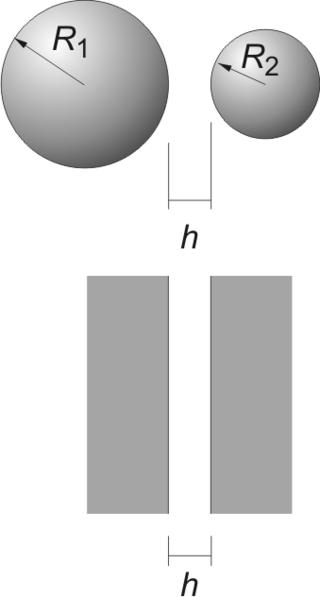
<span class="mw-page-title-main">Derjaguin approximation</span>

The Derjaguin approximation (or sometimes also referred to as the proximity approximation), named after the Russian scientist Boris Derjaguin, expresses the force profile acting between finite size bodies in terms of the force profile between two planar semi-infinite walls. This approximation is widely used to estimate forces between colloidal particles, as forces between two planar bodies are often much easier to calculate. The Derjaguin approximation expresses the force F(h) between two bodies as a function of the surface separation as

In condensed matter physics and physical chemistry, the Lifshitz theory of van der Waals forces, sometimes called the macroscopic theory of van der Waals forces, is a method proposed by Evgeny Mikhailovich Lifshitz in 1954 for treating van der Waals forces between bodies which does not assume pairwise additivity of the individual intermolecular forces; that is to say, the theory takes into account the influence of neighboring molecules on the interaction between every pair of molecules located in the two bodies, rather than treating each pair independently.

The Dresselhaus effect is a phenomenon in solid-state physics in which spin–orbit interaction causes energy bands to split. It is usually present in crystal systems lacking inversion symmetry. The effect is named after Gene Dresselhaus, who discovered this splitting in 1955.

PC-SAFT is an equation of state that is based on statistical associating fluid theory (SAFT). Like other SAFT equations of state, it makes use of chain and association terms developed by Chapman, et al from perturbation theory. However, unlike earlier SAFT equations of state that used unbonded spherical particles as a reference fluid, it uses spherical particles in the context of hard chains as reference fluid for the dispersion term.

References

↑ Szalewicz, Krzysztof (March 1, 2012). "Symmetry-adapted perturbation theory of intermolecular forces". WIREs Comput Mol Sci. 2 (2): 254–272. doi:10.1002/wcms.86. S2CID 97250676.
↑ Jeziorski, Bogumil; Moszynski, Robert; Szalewicz, Krzysztof (1994). "Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of van der Waals Complexes". Chem. Rev. 94 (7): 1887–1930. doi:10.1021/cr00031a008.
↑ Parker, Trent M.; Burns, Lori A.; Parrish, Robert M.; Ryno, Alden G.; Sherrill, C. David (2014). "Levels of symmetry adapted perturbation theory (SAPT). I. Efficiency and performance for interaction energies". J. Chem. Phys. 140 (9): 094106. Bibcode:2014JChPh.140i4106P. doi:10.1063/1.4867135. PMID 24606352.

This molecular physics–related article is a stub. You can help Wikipedia by expanding it.

This quantum chemistry-related article is a stub. You can help Wikipedia by expanding it.

This quantum mechanics-related article is a stub. You can help Wikipedia by expanding it.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Szalewicz, Krzysztof (March 1, 2012). "Symmetry-adapted perturbation theory of intermolecular forces". WIREs Comput Mol Sci. 2 (2): 254–272. doi:10.1002/wcms.86. S2CID 97250676.

[2] Jeziorski, Bogumil; Moszynski, Robert; Szalewicz, Krzysztof (1994). "Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of van der Waals Complexes". Chem. Rev. 94 (7): 1887–1930. doi:10.1021/cr00031a008.

[3] Parker, Trent M.; Burns, Lori A.; Parrish, Robert M.; Ryno, Alden G.; Sherrill, C. David (2014). "Levels of symmetry adapted perturbation theory (SAPT). I. Efficiency and performance for interaction energies". J. Chem. Phys. 140 (9): 094106. Bibcode:2014JChPh.140i4106P. doi:10.1063/1.4867135. PMID 24606352.

[1]

[2]

[3]