Termial

Last updated December 13, 2020

In mathematics, the termial of a positive integer $n$ , denoted by $n ?$ , is the sum of all positive integers less than or equal to $n$ . For example,

History

Since the 18th century, Leonhard Euler and some other mathematicians had been trying to extend the domain of the factorial function to real numbers or even complex numbers, and eventually put forward the Gamma function.^[3] In 1997, Donald E. Knuth introduced the termial function $n ?$ in his The Art of Computer Programming , as an analog of factorial in addition, so as to illustrate the meaning of domain extension.^[1]

Definition

The termial function is defined by the sum

n?=1+2+3+\cdots +(n-2)+(n-1)+n\,,

initially for integer $n \geq 1$ . This may be written in the Sigma sum notation as

n?=\sum _{i=1}^{n}i.

From these formulas, one may derive the recurrence relation

n?=n+(n-1)?\,.

For example, one has

{\begin{aligned}5?&=5+4?\\6?&=6+5?\\50?&=50+49?\end{aligned}}

and so on.

The termial function can be calculated using the summation formula for arithmetic sequence:

n?={\frac {n(n+1)}{2}}\,.

For example, $100?={\frac {100\times 101}{2}}=5050$ .

Termial of zero

In order for the recurrence relation to be extended to $n = 0$ , it is necessary to define

0?=0

so that

1?=1+0?=1.

Termial of a non-integer

The termial function can also be defined for non-integer values using the formula $n?={\frac {n(n+1)}{2}}$ .

For example, $\left({\frac {1}{2}}\right)?={\frac {3}{8}}$ .

Applications

Termial is less frequently used in mathematics, but still it has some uses in fields such as combinatorics.

For a set of $n$ distinct elements, the number of $2$ -combinations (i.e., number of ways to choose 2 of them) equals $(n - 1)?$ . This is to say

{n \choose 2}=(n-1)?\,.

In playing four fours, termial can be a useful tool to find the expression required, especially when the rules do not allow the use of decimal point and square root (which is because the numbers $0$ and $2$ are used invisibly). For example,

13=4?+4-4\div 4

18=4!+4?-4\times 4

Termial-like sum and functions

Double termial

Similar to double factorial^[4], The sum of all the odd integers up to some odd positive integer $n$ is called the double termial of $n$ , and denoted by $n ??$ . That is,

(2k-1)??=\sum _{i=1}^{k}(2i-1)=1+3+5+\cdots +(2k-3)+(2k-1)\,.

For example, $9??=1+3+5+7+9=25$ .

The sequence of double termial for $n = 1, 3, 5, 7,...$ is the square number sequence.^[5] It starts as

1, 4, 9, 16, 25, 36, 49, ... (sequence A000290 in the OEIS )

Primial

Primial can be introduced as an analog of primorial, and denoted by $n §$ . It is defined as the sum of prime numbers less than or equal to $n$ ^[6], i.e.

n\S =p_{\pi (n)}\S =\sum _{i=1}^{\pi (n)}p_{i}\,,

where $\pi (n)$ is the prime-counting function.

For example, $11\S =p_{5}\S =2+3+5+7+11=28$ .

The first few results are

0, 2, 5, 10, 17, 28, 41, ... (sequence A007504 in the OEIS )

Reciprocal termial

Reciprocal termial is defined as the sum of reciprocal of first $n$ positive integers. It is equal to the n-th harmonic number.^[7]

\sum _{i=1}^{n}{\frac {1}{i}}=1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}=H_{n}.

For example, $\sum _{i=1}^{3}{\frac {1}{i}}=1+{\frac {1}{2}}+{\frac {1}{3}}={\frac {11}{6}}.$

Related Research Articles

In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers $n \geq k \geq 0$ and is written $It is the coefficient of the x k term in the polynomial expansion of the binomial power (1 + x) n, and is given by the formula$

In mathematics, the Bernoulli numbers $B n$ are a sequence of rational numbers which occur frequently in number theory. The Bernoulli numbers appear in the Taylor series expansions of the tangent and hyperbolic tangent functions, in Faulhaber's formula for the sum of m-th powers of the first n positive integers, in the Euler–Maclaurin formula, and in expressions for certain values of the Riemann zeta function.

In mathematics, the factorial of a positive integer $n$ , denoted by $n!$ , is the product of all positive integers less than or equal to $n$ :

In mathematics, the Euler numbers are a sequence E_n of integers defined by the Taylor series expansion

In mathematics, Stirling numbers arise in a variety of analytic and combinatorial problems. They are named after James Stirling, who introduced them in the 18th century. Two different sets of numbers bear this name: the Stirling numbers of the first kind and the Stirling numbers of the second kind. Additionally, Lah numbers are sometimes referred to as Stirling numbers of the third kind. Each kind is detailed in its respective article, this one serving as a description of relations between them.

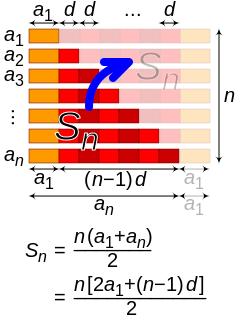
In mathematics, an arithmetic progression (AP) or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant. For instance, the sequence 5, 7, 9, 11, 13, 15,. .. is an arithmetic progression with a common difference of 2.

In mathematics, the falling factorial is defined as the polynomial

The Lucas numbers or Lucas series are an integer sequence named after the mathematician François Édouard Anatole Lucas (1842–91), who studied both that sequence and the closely related Fibonacci numbers. Lucas numbers and Fibonacci numbers form complementary instances of Lucas sequences.

In mathematics, and more particularly in number theory, primorial, denoted by “#”, is a function from natural numbers to natural numbers similar to the factorial function, but rather than successively multiplying positive integers, the function only multiplies prime numbers.

The fractional part or decimal part of a non‐negative real number $is the excess beyond that number's integer part. If the latter is defined as the largest integer not greater than x, called floor of x or , its fractional part can be written as:$

In mathematics, the double factorial or semifactorial of a number $n$ , denoted by $n ‼$ , is the product of all the integers from 1 up to $n$ that have the same parity as $n$ . That is,

In mathematics, a harshad number in a given number base is an integer that is divisible by the sum of its digits when written in that base. Harshad numbers in base $n$ are also known as $n$ -harshad numbers. Harshad numbers were defined by D. R. Kaprekar, a mathematician from India. The word "harshad" comes from the Sanskrit harṣa (joy) + da (give), meaning joy-giver. The term "Niven number" arose from a paper delivered by Ivan M. Niven at a conference on number theory in 1977. All integers between zero and $n$ are $n$ -harshad numbers.

A pentatope number is a number in the fifth cell of any row of Pascal's triangle starting with the 5-term row 1 4 6 4 1 either from left to right or from right to left.

The exponential factorial of a positive integer n, denoted by n$, is n raised to the power of n − 1, which in turn is raised to the power of n − 2, and so on and so forth. That is,

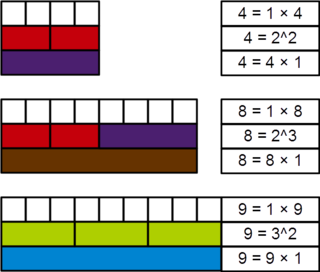
In mathematics, a perfect power is a positive integer that can be resolved into equal factors, and whose root can be exactly extracted, i.e., a positive integer that can be expressed as an integer power of another positive integer. More formally, n is a perfect power if there exist natural numbers m > 1, and k > 1 such that m^k = n. In this case, n may be called a perfect kth power. If k = 2 or k = 3, then n is called a perfect square or perfect cube, respectively. Sometimes 0 and 1 are also considered perfect powers.

In combinatorial mathematics, an alternating permutation of the set {1, 2, 3, ..., n} is a permutation (arrangement) of those numbers so that each entry is alternately greater or less than the preceding entry. For example, the five alternating permutations of {1, 2, 3, 4} are:

In mathematics, the Fibonacci numbers form a sequence defined recursively by:

In mathematics and computability theory, an elementary cellular automaton is a one-dimensional cellular automaton where there are two possible states and the rule to determine the state of a cell in the next generation depends only on the current state of the cell and its two immediate neighbors. There is an elementary cellular automaton which is capable of universal computation, and as such it is one of the simplest possible models of computation.

In mathematics, the Fibonorial $n! F$ , also called the Fibonacci factorial, where $n$ is a nonnegative integer, is defined as the product of the first $n$ positive Fibonacci numbers, i.e.

A mathematical constant is a key number whose value is fixed by an unambiguous definition, often referred to by a symbol, or by mathematicians' names to facilitate using it across multiple mathematical problems. Constants arise in many areas of mathematics, with constants such as $e$ and $π$ occurring in such diverse contexts as geometry, number theory, and calculus.

References

1 2 Donald E. Knuth (1997). The Art of Computer Programming: Volume 1: Fundamental Algorithms. 3rd Ed. Addison Wesley Longman, U.S.A. p. 48.
↑ Weisstein, Eric W. "Triangular Number". MathWorld-A Wolfram Web Resource. Retrieved 30 December 2018.
↑ Davis, P. J. (1959). "Leonhard Euler's Integral: A Historical Profile of the Gamma Function". American Mathematical Monthly . 66 (10): 849–869. doi:10.2307/2309786 . Retrieved 30 December 2018.
↑ Weisstein, Eric W. "Double Factorial". MathWorld-A Wolfram Web Resource. Retrieved 30 December 2018.
↑ Goodman, Len; Weisstein, Eric W. "Square Number". MathWorld-A Wolfram Web Resource. Retrieved 30 December 2018.
↑ Hardy, G. H. and Wright, E. M. (1979). An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 1–4, 17, 22, and 251.
↑ Graham, R. L.; Knuth, D. E.; and Patashnik, O. (1994). Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley. pp. 272–282.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[Donald-1] 1 2 Donald E. Knuth (1997). The Art of Computer Programming: Volume 1: Fundamental Algorithms. 3rd Ed. Addison Wesley Longman, U.S.A. p. 48.

[2] Weisstein, Eric W. "Triangular Number". MathWorld-A Wolfram Web Resource. Retrieved 30 December 2018.

[Davis-3] Davis, P. J. (1959). "Leonhard Euler's Integral: A Historical Profile of the Gamma Function". American Mathematical Monthly . 66 (10): 849–869. doi:10.2307/2309786 . Retrieved 30 December 2018.

[4] Weisstein, Eric W. "Double Factorial". MathWorld-A Wolfram Web Resource. Retrieved 30 December 2018.

[5] Goodman, Len; Weisstein, Eric W. "Square Number". MathWorld-A Wolfram Web Resource. Retrieved 30 December 2018.

[6] Hardy, G. H. and Wright, E. M. (1979). An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 1–4, 17, 22, and 251.

[7] Graham, R. L.; Knuth, D. E.; and Patashnik, O. (1994). Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley. pp. 272–282.

[1]

[2]

[3]

[4]

[5]

[6]

[7]