Test functions for optimization

In applied mathematics, test functions, known as artificial landscapes, are useful to evaluate characteristics of optimization algorithms, such as convergence rate, precision, robustness and general performance.

Here some test functions are presented with the aim of giving an idea about the different situations that optimization algorithms have to face when coping with these kinds of problems. In the first part, some objective functions for single-objective optimization cases are presented. In the second part, test functions with their respective Pareto fronts for multi-objective optimization problems (MOP) are given.

The artificial landscapes presented herein for single-objective optimization problems are taken from Bäck, ^[1] Haupt et al. ^[2] and from Rody Oldenhuis software. ^[3] Given the number of problems (55 in total), just a few are presented here.

The test functions used to evaluate the algorithms for MOP were taken from Deb, ^[4] Binh et al. ^[5] and Binh. ^[6] The software developed by Deb can be downloaded, ^[7] which implements the NSGA-II procedure with GAs, or the program posted on Internet, ^[8] which implements the NSGA-II procedure with ES.

Just a general form of the equation, a plot of the objective function, boundaries of the object variables and the coordinates of global minima are given herein.

Test functions for single-objective optimization

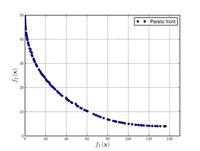
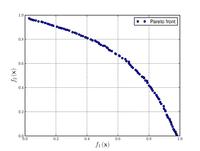
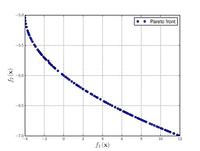
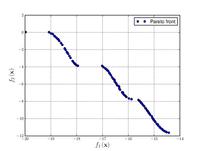
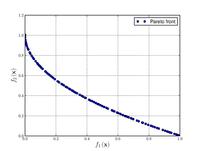
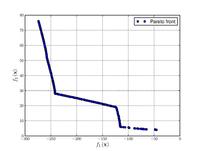
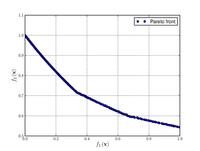
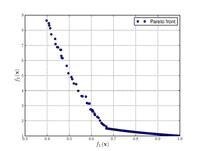
Name	Plot	Formula	Global minimum	Search domain
Rastrigin function		${\displaystyle f(\mathbf {x} )=An+\sum _{i=1}^{n}\left[x_{i}^{2}-A\cos(2\pi x_{i})\right]}$ ${\displaystyle {\text{where: }}A=10}$	${\displaystyle f(0,\dots ,0)=0}$	${\displaystyle -5.12\leq x_{i}\leq 5.12}$
Ackley function		${\displaystyle f(x,y)=-20\exp \left[-0.2{\sqrt {0.5\left(x^{2}+y^{2}\right)}}\right]}$ ${\displaystyle -\exp \left[0.5\left(\cos 2\pi x+\cos 2\pi y\right)\right]+e+20}$	${\displaystyle f(0,0)=0}$	${\displaystyle -5\leq x,y\leq 5}$
Sphere function		${\displaystyle f({\boldsymbol {x}})=\sum _{i=1}^{n}x_{i}^{2}}$	${\displaystyle f(x_{1},\dots ,x_{n})=f(0,\dots ,0)=0}$	${\displaystyle -\infty \leq x_{i}\leq \infty }$, ${\displaystyle 1\leq i\leq n}$
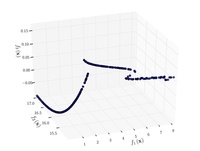
Rosenbrock function		${\displaystyle f({\boldsymbol {x}})=\sum _{i=1}^{n-1}\left[100\left(x_{i+1}-x_{i}^{2}\right)^{2}+\left(1-x_{i}\right)^{2}\right]}$	${\displaystyle {\text{Min}}={\begin{cases}n=2&\rightarrow \quad f(1,1)=0,\\n=3&\rightarrow \quad f(1,1,1)=0,\\n>3&\rightarrow \quad f(\underbrace {1,\dots ,1} _{n{\text{ times}}})=0\\\end{cases}}}$	${\displaystyle -\infty \leq x_{i}\leq \infty }$, ${\displaystyle 1\leq i\leq n}$
Beale function		${\displaystyle f(x,y)=\left(1.5-x+xy\right)^{2}+\left(2.25-x+xy^{2}\right)^{2}}$ ${\displaystyle +\left(2.625-x+xy^{3}\right)^{2}}$	${\displaystyle f(3,0.5)=0}$	${\displaystyle -4.5\leq x,y\leq 4.5}$
Goldstein–Price function		${\displaystyle f(x,y)=\left[1+\left(x+y+1\right)^{2}\left(19-14x+3x^{2}-14y+6xy+3y^{2}\right)\right]}$ ${\displaystyle \left[30+\left(2x-3y\right)^{2}\left(18-32x+12x^{2}+48y-36xy+27y^{2}\right)\right]}$	${\displaystyle f(0,-1)=3}$	${\displaystyle -2\leq x,y\leq 2}$
Booth function		${\displaystyle f(x,y)=\left(x+2y-7\right)^{2}+\left(2x+y-5\right)^{2}}$	${\displaystyle f(1,3)=0}$	${\displaystyle -10\leq x,y\leq 10}$
Bukin function N.6		${\displaystyle f(x,y)=100{\sqrt {\left|y-0.01x^{2}\right|}}+0.01\left|x+10\right|.\quad }$	${\displaystyle f(-10,1)=0}$	${\displaystyle -15\leq x\leq -5}$, ${\displaystyle -3\leq y\leq 3}$
Matyas function		${\displaystyle f(x,y)=0.26\left(x^{2}+y^{2}\right)-0.48xy}$	${\displaystyle f(0,0)=0}$	${\displaystyle -10\leq x,y\leq 10}$
Lévi function N.13		${\displaystyle f(x,y)=\sin ^{2}3\pi x+\left(x-1\right)^{2}\left(1+\sin ^{2}3\pi y\right)}$ ${\displaystyle +\left(y-1\right)^{2}\left(1+\sin ^{2}2\pi y\right)}$	${\displaystyle f(1,1)=0}$	${\displaystyle -10\leq x,y\leq 10}$
Griewank function		${\displaystyle f({\boldsymbol {x}})=1+{\frac {1}{4000}}\sum _{i=1}^{n}x_{i}^{2}-\prod _{i=1}^{n}P_{i}(x_{i})}$, where ${\displaystyle P_{i}(x_{i})=\cos \left({\frac {x_{i}}{\sqrt {i}}}\right)}$	${\displaystyle f(0,\dots ,0)=0}$	${\displaystyle -\infty \leq x_{i}\leq \infty }$, ${\displaystyle 1\leq i\leq n}$
Himmelblau's function		${\displaystyle f(x,y)=(x^{2}+y-11)^{2}+(x+y^{2}-7)^{2}.\quad }$	${\displaystyle {\text{Min}}={\begin{cases}f\left(3.0,2.0\right)&=0.0\\f\left(-2.805118,3.131312\right)&=0.0\\f\left(-3.779310,-3.283186\right)&=0.0\\f\left(3.584428,-1.848126\right)&=0.0\\\end{cases}}}$	${\displaystyle -5\leq x,y\leq 5}$
Three-hump camel function		${\displaystyle f(x,y)=2x^{2}-1.05x^{4}+{\frac {x^{6}}{6}}+xy+y^{2}}$	${\displaystyle f(0,0)=0}$	${\displaystyle -5\leq x,y\leq 5}$
Easom function		${\displaystyle f(x,y)=-\cos \left(x\right)\cos \left(y\right)\exp \left(-\left(\left(x-\pi \right)^{2}+\left(y-\pi \right)^{2}\right)\right)}$	${\displaystyle f(\pi ,\pi )=-1}$	${\displaystyle -100\leq x,y\leq 100}$
Cross-in-tray function		${\displaystyle f(x,y)=-0.0001\left[\left|\sin x\sin y\exp \left(\left|100-{\frac {\sqrt {x^{2}+y^{2}}}{\pi }}\right|\right)\right|+1\right]^{0.1}}$	${\displaystyle {\text{Min}}={\begin{cases}f\left(1.34941,-1.34941\right)&=-2.06261\\f\left(1.34941,1.34941\right)&=-2.06261\\f\left(-1.34941,1.34941\right)&=-2.06261\\f\left(-1.34941,-1.34941\right)&=-2.06261\\\end{cases}}}$	${\displaystyle -10\leq x,y\leq 10}$
Eggholder function [9] [10]		${\displaystyle f(x,y)=-\left(y+47\right)\sin {\sqrt {\left|{\frac {x}{2}}+\left(y+47\right)\right|}}-x\sin {\sqrt {\left|x-\left(y+47\right)\right|}}}$	${\displaystyle f(512,404.2319)=-959.6407}$	${\displaystyle -512\leq x,y\leq 512}$
Hölder table function		${\displaystyle f(x,y)=-\left|\sin x\cos y\exp \left(\left|1-{\frac {\sqrt {x^{2}+y^{2}}}{\pi }}\right|\right)\right|}$	${\displaystyle {\text{Min}}={\begin{cases}f\left(8.05502,9.66459\right)&=-19.2085\\f\left(-8.05502,9.66459\right)&=-19.2085\\f\left(8.05502,-9.66459\right)&=-19.2085\\f\left(-8.05502,-9.66459\right)&=-19.2085\end{cases}}}$	${\displaystyle -10\leq x,y\leq 10}$
McCormick function		${\displaystyle f(x,y)=\sin \left(x+y\right)+\left(x-y\right)^{2}-1.5x+2.5y+1}$	${\displaystyle f(-0.54719,-1.54719)=-1.9133}$	${\displaystyle -1.5\leq x\leq 4}$, ${\displaystyle -3\leq y\leq 4}$
Schaffer function N. 2		${\displaystyle f(x,y)=0.5+{\frac {\sin ^{2}\left(x^{2}-y^{2}\right)-0.5}{\left[1+0.001\left(x^{2}+y^{2}\right)\right]^{2}}}}$	${\displaystyle f(0,0)=0}$	${\displaystyle -100\leq x,y\leq 100}$
Schaffer function N. 4		${\displaystyle f(x,y)=0.5+{\frac {\cos ^{2}\left[\sin \left(\left|x^{2}-y^{2}\right|\right)\right]-0.5}{\left[1+0.001\left(x^{2}+y^{2}\right)\right]^{2}}}}$	${\displaystyle {\text{Min}}={\begin{cases}f\left(0,1.25313\right)&=0.292579\\f\left(0,-1.25313\right)&=0.292579\\f\left(1.25313,0\right)&=0.292579\\f\left(-1.25313,0\right)&=0.292579\end{cases}}}$	${\displaystyle -100\leq x,y\leq 100}$
Styblinski–Tang function		${\displaystyle f({\boldsymbol {x}})={\frac {\sum _{i=1}^{n}x_{i}^{4}-16x_{i}^{2}+5x_{i}}{2}}}$	${\displaystyle -39.16617n<f(\underbrace {-2.903534,\ldots ,-2.903534} _{n{\text{ times}}})<-39.16616n}$	${\displaystyle -5\leq x_{i}\leq 5}$, ${\displaystyle 1\leq i\leq n}$..
Shekel function		${\displaystyle f({\boldsymbol {x}})=\sum _{i=1}^{m}\;\left(c_{i}+\sum \limits _{j=1}^{n}(x_{j}-a_{ji})^{2}\right)^{-1}}$		${\displaystyle -\infty \leq x_{i}\leq \infty }$, ${\displaystyle 1\leq i\leq n}$

Test functions for constrained optimization

Name	Plot	Formula	Global minimum	Search domain
Rosenbrock function constrained to a disk [11]		${\displaystyle f(x,y)=(1-x)^{2}+100(y-x^{2})^{2}}$, subjected to: ${\displaystyle x^{2}+y^{2}\leq 2}$	${\displaystyle f(1.0,1.0)=0}$	${\displaystyle -1.5\leq x\leq 1.5}$, ${\displaystyle -1.5\leq y\leq 1.5}$
Mishra's Bird function - constrained [12] [13]		${\displaystyle f(x,y)=\sin(y)e^{\left[(1-\cos x)^{2}\right]}+\cos(x)e^{\left[(1-\sin y)^{2}\right]}+(x-y)^{2}}$, subjected to: ${\displaystyle (x+5)^{2}+(y+5)^{2}<25}$	${\displaystyle f(-3.1302468,-1.5821422)=-106.7645367}$	${\displaystyle -10\leq x\leq 0}$, ${\displaystyle -6.5\leq y\leq 0}$
Townsend function (modified) [14]		${\displaystyle f(x,y)=-[\cos((x-0.1)y)]^{2}-x\sin(3x+y)}$, subjected to:${\displaystyle x^{2}+y^{2}<\left[2\cos t-{\frac {1}{2}}\cos 2t-{\frac {1}{4}}\cos 3t-{\frac {1}{8}}\cos 4t\right]^{2}+[2\sin t]^{2}}$ where: t = Atan2(x,y)	${\displaystyle f(2.0052938,1.1944509)=-2.0239884}$	${\displaystyle -2.25\leq x\leq 2.25}$, ${\displaystyle -2.5\leq y\leq 1.75}$
Keane's bump function [15]		${\displaystyle f({\boldsymbol {x}})=-\left|{\frac {\left[\sum _{i=1}^{m}\cos ^{4}(x_{i})-2\prod _{i=1}^{m}\cos ^{2}(x_{i})\right]}{{\left(\sum _{i=1}^{m}ix_{i}^{2}\right)}^{0.5}}}\right|}$, subjected to: ${\displaystyle 0.75-\prod _{i=1}^{m}x_{i}<0}$, and ${\displaystyle \sum _{i=1}^{m}x_{i}-7.5m<0}$	${\displaystyle f((1.60025376,0.468675907))=-0.364979746}$	${\displaystyle 0<x_{i}<10}$

Test functions for multi-objective optimization

^{[ further explanation needed ]}

Name	Plot	Functions	Constraints	Search domain
Binh and Korn function: [5]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=4x^{2}+4y^{2}\\f_{2}\left(x,y\right)=\left(x-5\right)^{2}+\left(y-5\right)^{2}\\\end{cases}}}$	${\displaystyle {\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)=\left(x-5\right)^{2}+y^{2}\leq 25\\g_{2}\left(x,y\right)=\left(x-8\right)^{2}+\left(y+3\right)^{2}\geq 7.7\\\end{cases}}}$	${\displaystyle 0\leq x\leq 5}$, ${\displaystyle 0\leq y\leq 3}$
Chankong and Haimes function: [16]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=2+\left(x-2\right)^{2}+\left(y-1\right)^{2}\\f_{2}\left(x,y\right)=9x-\left(y-1\right)^{2}\\\end{cases}}}$	${\displaystyle {\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)=x^{2}+y^{2}\leq 225\\g_{2}\left(x,y\right)=x-3y+10\leq 0\\\end{cases}}}$	${\displaystyle -20\leq x,y\leq 20}$
Fonseca–Fleming function: [17]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=1-\exp \left[-\sum _{i=1}^{n}\left(x_{i}-{\frac {1}{\sqrt {n}}}\right)^{2}\right]\\f_{2}\left({\boldsymbol {x}}\right)=1-\exp \left[-\sum _{i=1}^{n}\left(x_{i}+{\frac {1}{\sqrt {n}}}\right)^{2}\right]\\\end{cases}}}$		${\displaystyle -4\leq x_{i}\leq 4}$, ${\displaystyle 1\leq i\leq n}$
Test function 4: [6]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=x^{2}-y\\f_{2}\left(x,y\right)=-0.5x-y-1\\\end{cases}}}$	${\displaystyle {\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)=6.5-{\frac {x}{6}}-y\geq 0\\g_{2}\left(x,y\right)=7.5-0.5x-y\geq 0\\g_{3}\left(x,y\right)=30-5x-y\geq 0\\\end{cases}}}$	${\displaystyle -7\leq x,y\leq 4}$
Kursawe function: [18]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=\sum _{i=1}^{2}\left[-10\exp \left(-0.2{\sqrt {x_{i}^{2}+x_{i+1}^{2}}}\right)\right]\\&\\f_{2}\left({\boldsymbol {x}}\right)=\sum _{i=1}^{3}\left[\left|x_{i}\right|^{0.8}+5\sin \left(x_{i}^{3}\right)\right]\\\end{cases}}}$		${\displaystyle -5\leq x_{i}\leq 5}$, ${\displaystyle 1\leq i\leq 3}$.
Schaffer function N. 1: [19]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x\right)=x^{2}\\f_{2}\left(x\right)=\left(x-2\right)^{2}\\\end{cases}}}$		${\displaystyle -A\leq x\leq A}$. Values of ${\displaystyle A}$ from ${\displaystyle 10}$ to ${\displaystyle 10^{5}}$ have been used successfully. Higher values of ${\displaystyle A}$ increase the difficulty of the problem.
Schaffer function N. 2:		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x\right)={\begin{cases}-x,&{\text{if }}x\leq 1\\x-2,&{\text{if }}1<x\leq 3\\4-x,&{\text{if }}3<x\leq 4\\x-4,&{\text{if }}x>4\\\end{cases}}\\f_{2}\left(x\right)=\left(x-5\right)^{2}\\\end{cases}}}$		${\displaystyle -5\leq x\leq 10}$.
Poloni's two objective function:		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=\left[1+\left(A_{1}-B_{1}\left(x,y\right)\right)^{2}+\left(A_{2}-B_{2}\left(x,y\right)\right)^{2}\right]\\f_{2}\left(x,y\right)=\left(x+3\right)^{2}+\left(y+1\right)^{2}\\\end{cases}}}$ ${\displaystyle {\text{where}}={\begin{cases}A_{1}=0.5\sin \left(1\right)-2\cos \left(1\right)+\sin \left(2\right)-1.5\cos \left(2\right)\\A_{2}=1.5\sin \left(1\right)-\cos \left(1\right)+2\sin \left(2\right)-0.5\cos \left(2\right)\\B_{1}\left(x,y\right)=0.5\sin \left(x\right)-2\cos \left(x\right)+\sin \left(y\right)-1.5\cos \left(y\right)\\B_{2}\left(x,y\right)=1.5\sin \left(x\right)-\cos \left(x\right)+2\sin \left(y\right)-0.5\cos \left(y\right)\end{cases}}}$		${\displaystyle -\pi \leq x,y\leq \pi }$
Zitzler–Deb–Thiele's function N. 1: [20]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=x_{1}\\f_{2}\left({\boldsymbol {x}}\right)=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)=1+{\frac {9}{29}}\sum _{i=2}^{30}x_{i}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)=1-{\sqrt {\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}}\\\end{cases}}}$		${\displaystyle 0\leq x_{i}\leq 1}$, ${\displaystyle 1\leq i\leq 30}$.
Zitzler–Deb–Thiele's function N. 2: [20]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=x_{1}\\f_{2}\left({\boldsymbol {x}}\right)=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)=1+{\frac {9}{29}}\sum _{i=2}^{30}x_{i}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)=1-\left({\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}\right)^{2}\\\end{cases}}}$		${\displaystyle 0\leq x_{i}\leq 1}$, ${\displaystyle 1\leq i\leq 30}$.
Zitzler–Deb–Thiele's function N. 3: [20]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=x_{1}\\f_{2}\left({\boldsymbol {x}}\right)=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)=1+{\frac {9}{29}}\sum _{i=2}^{30}x_{i}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)=1-{\sqrt {\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}}-\left({\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}\right)\sin \left(10\pi f_{1}\left({\boldsymbol {x}}\right)\right)\end{cases}}}$		${\displaystyle 0\leq x_{i}\leq 1}$, ${\displaystyle 1\leq i\leq 30}$.
Zitzler–Deb–Thiele's function N. 4: [20]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=x_{1}\\f_{2}\left({\boldsymbol {x}}\right)=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)=91+\sum _{i=2}^{10}\left(x_{i}^{2}-10\cos \left(4\pi x_{i}\right)\right)\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)=1-{\sqrt {\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}}\end{cases}}}$		${\displaystyle 0\leq x_{1}\leq 1}$, ${\displaystyle -5\leq x_{i}\leq 5}$, ${\displaystyle 2\leq i\leq 10}$
Zitzler–Deb–Thiele's function N. 6: [20]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=1-\exp \left(-4x_{1}\right)\sin ^{6}\left(6\pi x_{1}\right)\\f_{2}\left({\boldsymbol {x}}\right)=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)=1+9\left[{\frac {\sum _{i=2}^{10}x_{i}}{9}}\right]^{0.25}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)=1-\left({\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}\right)^{2}\\\end{cases}}}$		${\displaystyle 0\leq x_{i}\leq 1}$, ${\displaystyle 1\leq i\leq 10}$.
Osyczka and Kundu function: [21]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=-25\left(x_{1}-2\right)^{2}-\left(x_{2}-2\right)^{2}-\left(x_{3}-1\right)^{2}-\left(x_{4}-4\right)^{2}-\left(x_{5}-1\right)^{2}\\f_{2}\left({\boldsymbol {x}}\right)=\sum _{i=1}^{6}x_{i}^{2}\\\end{cases}}}$	${\displaystyle {\text{s.t.}}={\begin{cases}g_{1}\left({\boldsymbol {x}}\right)=x_{1}+x_{2}-2\geq 0\\g_{2}\left({\boldsymbol {x}}\right)=6-x_{1}-x_{2}\geq 0\\g_{3}\left({\boldsymbol {x}}\right)=2-x_{2}+x_{1}\geq 0\\g_{4}\left({\boldsymbol {x}}\right)=2-x_{1}+3x_{2}\geq 0\\g_{5}\left({\boldsymbol {x}}\right)=4-\left(x_{3}-3\right)^{2}-x_{4}\geq 0\\g_{6}\left({\boldsymbol {x}}\right)=\left(x_{5}-3\right)^{2}+x_{6}-4\geq 0\end{cases}}}$	${\displaystyle 0\leq x_{1},x_{2},x_{6}\leq 10}$, ${\displaystyle 1\leq x_{3},x_{5}\leq 5}$, ${\displaystyle 0\leq x_{4}\leq 6}$.
CTP1 function (2 variables): [4] [22]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=x\\f_{2}\left(x,y\right)=\left(1+y\right)\exp \left(-{\frac {x}{1+y}}\right)\end{cases}}}$	${\displaystyle {\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)={\frac {f_{2}\left(x,y\right)}{0.858\exp \left(-0.541f_{1}\left(x,y\right)\right)}}\geq 1\\g_{2}\left(x,y\right)={\frac {f_{2}\left(x,y\right)}{0.728\exp \left(-0.295f_{1}\left(x,y\right)\right)}}\geq 1\end{cases}}}$	${\displaystyle 0\leq x,y\leq 1}$.
Constr-Ex problem: [4]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=x\\f_{2}\left(x,y\right)={\frac {1+y}{x}}\\\end{cases}}}$	${\displaystyle {\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)=y+9x\geq 6\\g_{2}\left(x,y\right)=-y+9x\geq 1\\\end{cases}}}$	${\displaystyle 0.1\leq x\leq 1}$, ${\displaystyle 0\leq y\leq 5}$
Viennet function:		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=0.5\left(x^{2}+y^{2}\right)+\sin \left(x^{2}+y^{2}\right)\\f_{2}\left(x,y\right)={\frac {\left(3x-2y+4\right)^{2}}{8}}+{\frac {\left(x-y+1\right)^{2}}{27}}+15\\f_{3}\left(x,y\right)={\frac {1}{x^{2}+y^{2}+1}}-1.1\exp \left(-\left(x^{2}+y^{2}\right)\right)\\\end{cases}}}$		${\displaystyle -3\leq x,y\leq 3}$.

References

1. Bäck, Thomas (1995). Evolutionary algorithms in theory and practice : evolution strategies, evolutionary programming, genetic algorithms. Oxford: Oxford University Press. p. 328. ISBN   978-0-19-509971-3.
2. Haupt, Randy L. Haupt, Sue Ellen (2004). Practical genetic algorithms with CD-Rom (2nd ed.). New York: J. Wiley. ISBN   978-0-471-45565-3.
3. Oldenhuis, Rody. "Many test functions for global optimizers". Mathworks. Retrieved 1 November 2012.
4. Deb, Kalyanmoy (2002) Multiobjective optimization using evolutionary algorithms (Repr. ed.). Chichester [u.a.]: Wiley. ISBN   0-471-87339-X.
5. Binh T. and Korn U. (1997) MOBES: A Multiobjective Evolution Strategy for Constrained Optimization Problems. In: Proceedings of the Third International Conference on Genetic Algorithms. Czech Republic. pp. 176–182
6. Binh T. (1999) A multiobjective evolutionary algorithm. The study cases. Technical report. Institute for Automation and Communication. Barleben, Germany
7. Deb K. (2011) Software for multi-objective NSGA-II code in C. Available at URL: https://www.iitk.ac.in/kangal/codes.shtml
8. Ortiz, Gilberto A. "Multi-objective optimization using ES as Evolutionary Algorithm". Mathworks. Retrieved 1 November 2012.
9. Whitley, Darrell; Rana, Soraya; Dzubera, John; Mathias, Keith E. (1996). "Evaluating evolutionary algorithms". Artificial Intelligence. 85 (1–2). Elsevier BV: 264. doi: 10.1016/0004-3702(95)00124-7 . ISSN   0004-3702.
10. Vanaret C. (2015) Hybridization of interval methods and evolutionary algorithms for solving difficult optimization problems. PhD thesis. Ecole Nationale de l'Aviation Civile. Institut National Polytechnique de Toulouse, France.
11. "Solve a Constrained Nonlinear Problem - MATLAB & Simulink". www.mathworks.com. Retrieved 2017-08-29.
12. "Bird Problem (Constrained) | Phoenix Integration". Archived from the original on 2016-12-29. Retrieved 2017-08-29.
13. Mishra, Sudhanshu (2006). "Some new test functions for global optimization and performance of repulsive particle swarm method". MPRA Paper.
14. Townsend, Alex (January 2014). "Constrained optimization in Chebfun". chebfun.org. Retrieved 2017-08-29.
15. Mishra, Sudhanshu (5 May 2007). "Minimization of Keane's Bump Function by the Repulsive Particle Swarm and the Differential Evolution Methods". MPRA Paper. University Library of Munich, Germany.
16. Chankong, Vira; Haimes, Yacov Y. (1983). Multiobjective decision making. Theory and methodology. North Holland. ISBN   0-444-00710-5.
17. Fonseca, C. M.; Fleming, P. J. (1995). "An Overview of Evolutionary Algorithms in Multiobjective Optimization". Evol Comput . 3 (1): 1–16. CiteSeerX   10.1.1.50.7779 . doi:10.1162/evco.1995.3.1.1. S2CID   8530790.
18. F. Kursawe, “A variant of evolution strategies for vector optimization,” in PPSN I, Vol 496 Lect Notes in Comput Sc. Springer-Verlag, 1991, pp. 193–197.
19. Schaffer, J. David (1984). "Multiple Objective Optimization with Vector Evaluated Genetic Algorithms". In G.J.E Grefensette; J.J. Lawrence Erlbraum (eds.). Proceedings of the First International Conference on Genetic Algorithms. OCLC   20004572.
20. Deb, Kalyan; Thiele, L.; Laumanns, Marco; Zitzler, Eckart (2002). "Scalable multi-objective optimization test problems". Proceedings of the 2002 Congress on Evolutionary Computation. CEC'02 (Cat. No.02TH8600). Vol. 1. pp. 825–830. doi:10.1109/CEC.2002.1007032. ISBN   0-7803-7282-4. S2CID   61001583.
21. Osyczka, A.; Kundu, S. (1 October 1995). "A new method to solve generalized multicriteria optimization problems using the simple genetic algorithm". Structural Optimization. 10 (2): 94–99. doi:10.1007/BF01743536. ISSN   1615-1488. S2CID   123433499.
22. Jimenez, F.; Gomez-Skarmeta, A. F.; Sanchez, G.; Deb, K. (May 2002). "An evolutionary algorithm for constrained multi-objective optimization". Proceedings of the 2002 Congress on Evolutionary Computation. CEC'02 (Cat. No.02TH8600). Vol. 2. pp. 1133–1138. doi:10.1109/CEC.2002.1004402. ISBN   0-7803-7282-4. S2CID   56563996.

External links

• landscapes