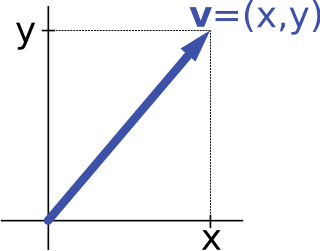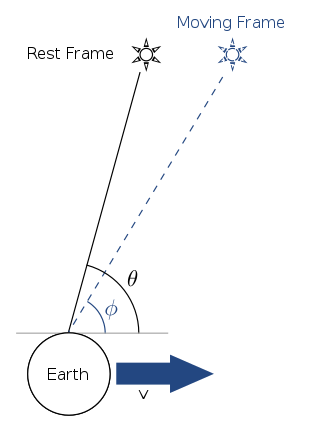
In astronomy, aberration is a phenomenon which produces an apparent motion of celestial objects about their true positions, dependent on the velocity of the observer. It causes objects to appear to be displaced towards the direction of motion of the observer compared to when the observer is stationary. The change in angle is of the order of v/c where c is the speed of light and v the velocity of the observer. In the case of "stellar" or "annual" aberration, the apparent position of a star to an observer on Earth varies periodically over the course of a year as the Earth's velocity changes as it revolves around the Sun, by a maximum angle of approximately 20 arcseconds in right ascension or declination.
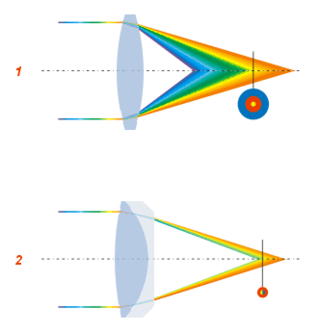
In optics, aberration is a property of optical systems, such as lenses, that causes light to be spread out over some region of space rather than focused to a point. Aberrations cause the image formed by a lens to be blurred or distorted, with the nature of the distortion depending on the type of aberration. Aberration can be defined as a departure of the performance of an optical system from the predictions of paraxial optics. In an imaging system, it occurs when light from one point of an object does not converge into a single point after transmission through the system. Aberrations occur because the simple paraxial theory is not a completely accurate model of the effect of an optical system on light, rather than due to flaws in the optical elements.

A centripetal force is a force that makes a body follow a curved path. The direction of the centripetal force is always orthogonal to the motion of the body and towards the fixed point of the instantaneous center of curvature of the path. Isaac Newton described it as "a force by which bodies are drawn or impelled, or in any way tend, towards a point as to a centre". In the theory of Newtonian mechanics, gravity provides the centripetal force causing astronomical orbits.

Diffraction is the interference or bending of waves around the corners of an obstacle or through an aperture into the region of geometrical shadow of the obstacle/aperture. The diffracting object or aperture effectively becomes a secondary source of the propagating wave. Italian scientist Francesco Maria Grimaldi coined the word diffraction and was the first to record accurate observations of the phenomenon in 1660.

Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behaviour of visible, ultraviolet, and infrared light. Because light is an electromagnetic wave, other forms of electromagnetic radiation such as X-rays, microwaves, and radio waves exhibit similar properties.

In optics, the numerical aperture (NA) of an optical system is a dimensionless number that characterizes the range of angles over which the system can accept or emit light. By incorporating index of refraction in its definition, NA has the property that it is constant for a beam as it goes from one material to another, provided there is no refractive power at the interface. The exact definition of the term varies slightly between different areas of optics. Numerical aperture is commonly used in microscopy to describe the acceptance cone of an objective, and in fiber optics, in which it describes the range of angles within which light that is incident on the fiber will be transmitted along it.
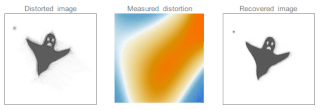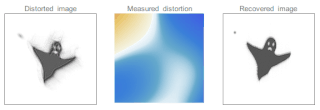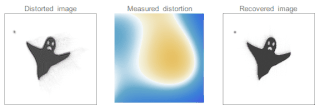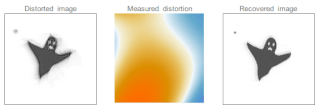
Adaptive optics (AO) is a technique of precisely deforming a mirror in order to compensate light distortion. It is used in astronomical telescopes and laser communication systems to remove the effects of atmospheric distortion, in microscopy, optical fabrication and in retinal imaging systems to reduce optical aberrations. Adaptive optics works by measuring the distortions in a wavefront and compensating for them with a device that corrects those errors such as a deformable mirror or a liquid crystal array.

Angular resolution describes the ability of any image-forming device such as an optical or radio telescope, a microscope, a camera, or an eye, to distinguish small details of an object, thereby making it a major determinant of image resolution. It is used in optics applied to light waves, in antenna theory applied to radio waves, and in acoustics applied to sound waves. The colloquial use of the term "resolution" sometimes causes confusion; when an optical system is said to have a high resolution or high angular resolution, it means that the perceived distance, or actual angular distance, between resolved neighboring objects is small. The value that quantifies this property, θ, which is given by the Rayleigh criterion, is low for a system with a high resolution. The closely related term spatial resolution refers to the precision of a measurement with respect to space, which is directly connected to angular resolution in imaging instruments. The Rayleigh criterion shows that the minimum angular spread that can be resolved by an image forming system is limited by diffraction to the ratio of the wavelength of the waves to the aperture width. For this reason, high resolution imaging systems such as astronomical telescopes, long distance telephoto camera lenses and radio telescopes have large apertures.
This is a list of some vector calculus formulae for working with common curvilinear coordinate systems.

Note: This page uses common physics notation for spherical coordinates, in which is the angle between the z axis and the radius vector connecting the origin to the point in question, while is the angle between the projection of the radius vector onto the x-y plane and the x axis. Several other definitions are in use, and so care must be taken in comparing different sources.
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when plane waves are incident on a diffracting object, and the diffraction pattern is viewed at a sufficiently long distance from the object, and also when it is viewed at the focal plane of an imaging lens. In contrast, the diffraction pattern created near the diffracting object and is given by the Fresnel diffraction equation.

In mathematics, the Zernike polynomials are a sequence of polynomials that are orthogonal on the unit disk. Named after optical physicist Frits Zernike, laureate of the 1953 Nobel Prize in Physics and the inventor of phase-contrast microscopy, they play important roles in various optics branches such as beam optics and imaging.
In optics, the Fresnel diffraction equation for near-field diffraction is an approximation of the Kirchhoff–Fresnel diffraction that can be applied to the propagation of waves in the near field. It is used to calculate the diffraction pattern created by waves passing through an aperture or around an object, when viewed from relatively close to the object. In contrast the diffraction pattern in the far field region is given by the Fraunhofer diffraction equation.

In mathematics (specifically multivariable calculus), a multiple integral is a definite integral of a function of several real variables, for instance, f(x, y) or f(x, y, z). Integrals of a function of two variables over a region in (the real-number plane) are called double integrals, and integrals of a function of three variables over a region in (real-number 3D space) are called triple integrals. For multiple integrals of a single-variable function, see the Cauchy formula for repeated integration.
In optics, piston is the mean value of a wavefront or phase profile across the pupil of an optical system. The piston coefficient is typically expressed in wavelengths of light at a particular wavelength. Its main use is in curve-fitting wavefronts with Cartesian polynomials or Zernike polynomials.
In mathematics and physics, vector notation is a commonly used notation for representing vectors, which may be Euclidean vectors, or more generally, members of a vector space.

The neutral axis is an axis in the cross section of a beam or shaft along which there are no longitudinal stresses or strains. Building trades workers should have a basic understanding of the concept and follow industry rules and guidelines, to avoid dangerously compromising the structural safety of a building.
In mathematics, log-polar coordinates is a coordinate system in two dimensions, where a point is identified by two numbers, one for the logarithm of the distance to a certain point, and one for an angle. Log-polar coordinates are closely connected to polar coordinates, which are usually used to describe domains in the plane with some sort of rotational symmetry. In areas like harmonic and complex analysis, the log-polar coordinates are more canonical than polar coordinates.
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens.
The eye, like any other optical system, suffers from a number of specific optical aberrations. The optical quality of the eye is limited by optical aberrations, diffraction and scatter. Correction of spherocylindrical refractive errors has been possible for nearly two centuries following Airy's development of methods to measure and correct ocular astigmatism. It has only recently become possible to measure the aberrations of the eye and with the advent of refractive surgery it might be possible to correct certain types of irregular astigmatism.