Related Research Articles

In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally,

In statistics, canonical-correlation analysis (CCA), also called canonical variates analysis, is a way of inferring information from cross-covariance matrices. If we have two vectors X = (X1, ..., Xn) and Y = (Y1, ..., Ym) of random variables, and there are correlations among the variables, then canonical-correlation analysis will find linear combinations of X and Y which have maximum correlation with each other. T. R. Knapp notes that "virtually all of the commonly encountered parametric tests of significance can be treated as special cases of canonical-correlation analysis, which is the general procedure for investigating the relationships between two sets of variables." The method was first introduced by Harold Hotelling in 1936, although in the context of angles between flats the mathematical concept was published by Jordan in 1875.

NumPy is a library for the Python programming language, adding support for large, multi-dimensional arrays and matrices, along with a large collection of high-level mathematical functions to operate on these arrays. The ancestor of NumPy, Numeric, was originally created by Jim Hugunin with contributions from several other developers. In 2005, Travis Oliphant created NumPy by incorporating features of the competing Numarray into Numeric, with extensive modifications. NumPy is open-source software and has many contributors. NumPy is a NumFOCUS fiscally sponsored project.
In mathematics, the Hessian matrix or Hessian is a square matrix of second-order partial derivatives of a scalar-valued function, or scalar field. It describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named after him. Hesse originally used the term "functional determinants".
In computer science, array programming refers to solutions which allow the application of operations to an entire set of values at once. Such solutions are commonly used in scientific and engineering settings.
In mathematics, matrix calculus is a specialized notation for doing multivariable calculus, especially over spaces of matrices. It collects the various partial derivatives of a single function with respect to many variables, and/or of a multivariate function with respect to a single variable, into vectors and matrices that can be treated as single entities. This greatly simplifies operations such as finding the maximum or minimum of a multivariate function and solving systems of differential equations. The notation used here is commonly used in statistics and engineering, while the tensor index notation is preferred in physics.
In numerical optimization, the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm is an iterative method for solving unconstrained nonlinear optimization problems. Like the related Davidon–Fletcher–Powell method, BFGS determines the descent direction by preconditioning the gradient with curvature information. It does so by gradually improving an approximation to the Hessian matrix of the loss function, obtained only from gradient evaluations via a generalized secant method.
Semidefinite programming (SDP) is a subfield of convex optimization concerned with the optimization of a linear objective function over the intersection of the cone of positive semidefinite matrices with an affine space, i.e., a spectrahedron.
Limited-memory BFGS is an optimization algorithm in the family of quasi-Newton methods that approximates the Broyden–Fletcher–Goldfarb–Shanno algorithm (BFGS) using a limited amount of computer memory. It is a popular algorithm for parameter estimation in machine learning. The algorithm's target problem is to minimize over unconstrained values of the real-vector where is a differentiable scalar function.
The TOMLAB Optimization Environment is a modeling platform for solving applied optimization problems in MATLAB.
The PROPT MATLAB Optimal Control Software is a new generation platform for solving applied optimal control and parameters estimation problems.

In mathematics, a matrix is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object.
In computer science, an array type is a data type that represents a collection of elements, each selected by one or more indices that can be computed at run time during program execution. Such a collection is usually called an array variable, array value, or simply array. By analogy with the mathematical concepts vector and matrix, array types with one and two indices are often called vector type and matrix type, respectively. More generally, a multidimensional array type can be called a tensor type.
Locally Optimal Block Preconditioned Conjugate Gradient (LOBPCG) is a matrix-free method for finding the largest eigenvalues and the corresponding eigenvectors of a symmetric generalized eigenvalue problem
A sum-of-squares optimization program is an optimization problem with a linear cost function and a particular type of constraint on the decision variables. These constraints are of the form that when the decision variables are used as coefficients in certain polynomials, those polynomials should have the polynomial SOS property. When fixing the maximum degree of the polynomials involved, sum-of-squares optimization is also known as the Lasserre hierarchy of relaxations in semidefinite programming.
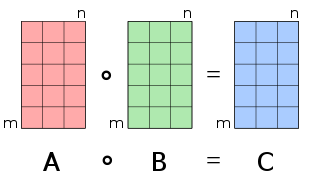
In mathematics, the Hadamard product is a binary operation that takes two matrices of the same dimensions and produces another matrix of the same dimension as the operands, where each element i, j is the product of elements i, j of the original two matrices. It is to be distinguished from the more common matrix product. It is attributed to, and named after, either French mathematician Jacques Hadamard or German Russian mathematician Issai Schur.
In mathematics, low-rank approximation is a minimization problem, in which the cost function measures the fit between a given matrix and an approximating matrix, subject to a constraint that the approximating matrix has reduced rank. The problem is used for mathematical modeling and data compression. The rank constraint is related to a constraint on the complexity of a model that fits the data. In applications, often there are other constraints on the approximating matrix apart from the rank constraint, e.g., non-negativity and Hankel structure.
In machine learning, feature hashing, also known as the hashing trick, is a fast and space-efficient way of vectorizing features, i.e. turning arbitrary features into indices in a vector or matrix. It works by applying a hash function to the features and using their hash values as indices directly, rather than looking the indices up in an associative array. This trick is often attributed to Weinberger et al., but there exists a much earlier description of this method published by John Moody in 1989.
Artelys Knitro is a commercial software package for solving large scale nonlinear mathematical optimization problems.
References
- ↑ Rutquist, Per; M. M. Edvall (Nov 2008). User's Manual for TOMLAB (PDF). Pullman, WA: Tomlab Optimization Inc.
- ↑ "Airline Hub Location", TOMSYM Home Page April, 2009.